一 实验目的
- 编写直线段、多边形裁剪算法
- 熟悉Cohen-Sutherland算法、中值分割算法和Liang-Barsky算法的裁剪
二 实验算法理论分析
Cohen-Sutherland算法:



中值分割算法:
与CS算法一样,首先对直线段端点进行编码,并把线段与窗口的关系一样分为3种情况:全在、完全不在、线段和窗口有交点,并对前两种情况进行一样的处理。对于第3种情况,则用中点分割的方法简单地把线段等分为两段,对两段重复上述测试处理,直至每条线段完全在窗口内和完全在窗口外。
可行性分析:计算机屏幕是有限的,比如1024×768个像素,x方向是2的10次方。所以这样一直二分下去的话,最多分10次。分到第十次的时候,就到像素级了,就不用再分了。所以最多循环10次。

Liang-Barsky算法:


三 实验内容
1:用Cohen-Sutherland算法实现直线段裁剪
实验结果如下图所示:
第一步:依次输入A点的横坐标和纵坐标、B点的横坐标和纵坐标(此处以【0,0】为A点坐标,【400,400】为B点坐标为例)。

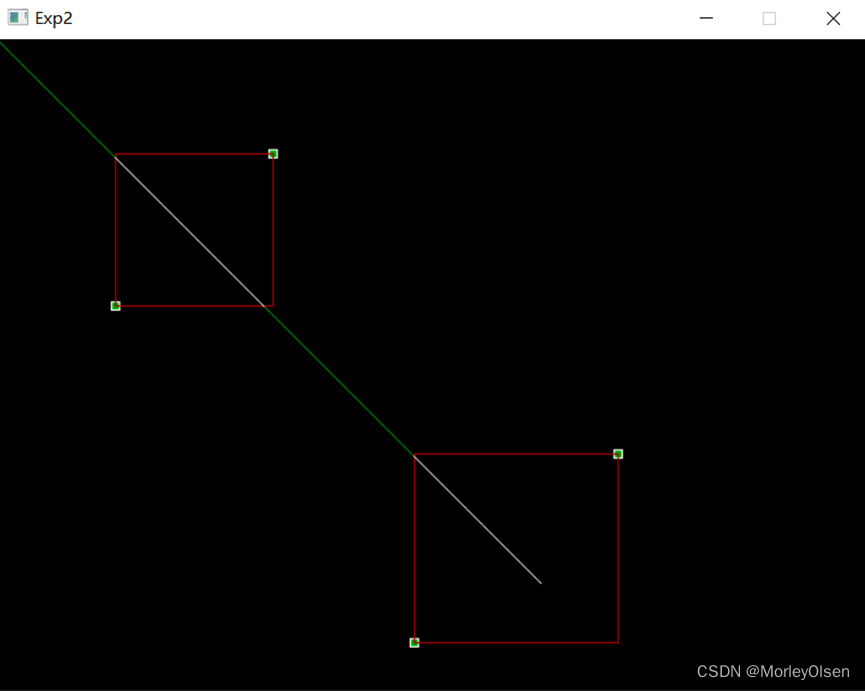
第二步:用户勾选需要裁剪的红色框,并将存在于矩形框内的AB线段用白色部分展示出来(此处以用户第一次点击为矩形框的左下位置,第二次点击为矩形框的右上位置为例)。
裁剪前:

裁剪后:

2:用中值分割算法实现直线段裁剪
实验结果如下图所示:
第一步:依次输入A点的横坐标和纵坐标、B点的横坐标和纵坐标(此处以【0,0】为A点坐标,【400,400】为B点坐标为例)。

第二步:用户勾选需要裁剪的红色框,并将存在于矩形框内的AB线段用白色部分展示出来(此处以用户第一次点击为矩形框的左下位置,第二次点击为矩形框的右上位置为例)。
裁剪前:

裁剪后:
3:用Liang-Barsky算法实现直线段裁剪
实验结果如下图所示:
第一步:依次输入A点的横坐标和纵坐标、B点的横坐标和纵坐标(此处以【0,0】为A点坐标,【400,250】为B点坐标为例)。

第二步:用户勾选需要裁剪的红色框,并将存在于矩形框内的AB线段用白色部分展示出来(此处以用户第一次点击为矩形框的左下位置,第二次点击为矩形框的右上位置为例)。
裁剪前:

裁剪后:

四 程序说明
Project中程序的调用:
将当前cpp文件的属性——常规——从生成中排除中选择否,其他文件选择是,即可运行当前的cpp文件
| 1题 |
| // // 程序名称:CS裁剪 // 功 能:用Cohen-Sutherland算法实现直线段裁剪 // 编译环境:VS2019,EasyX_20220116 // 最后修改:2022-3-17 #include <graphics.h> #include <conio.h> #include <iostream> using namespace std; #define LEFT 1 #define RIGHT 2 #define BOTTOM 4 #define TOP 8 int XL, XR, YB, YT; int encode(float x, float y, int* code) { int c = 0; if (x < XL) { c = c | LEFT; } else if (x > XR) { c = c | RIGHT; } if (y < YB) { c = c | BOTTOM;; } else if (y > YT) { c = c | TOP; } *code = c; return 0; } int CSLineClip(float x1, float y1, float x2, float y2) { int code1, code2, code; float x, y; encode(x1, y1, &code1); encode(x2, y2, &code2); while (code1 != 0 || code2 != 0) { if ((code1 & code2) != 0) { return 0; } code = code1; if (code1 == 0) { code = code2; } if ((LEFT & code) != 0) { x = XL; y = y1 + (y2 - y1) * (XL - x1) / (x2 - x1); } else if ((RIGHT & code) != 0) { x = XR; y = y1 + (y2 - y1) * (XR - x1) / (x2 - x1); } else if ((BOTTOM & code) != 0) { y = YB; x = x1 + (x2 - x1) * (YB - y1) / (y2 - y1); } else if ((TOP & code) != 0) { y = YT; x = x1 + (x2 - x1) * (YT - y1) / (y2 - y1); } // if (code == code1) { x1 = x; y1 = y; encode(x, y, &code1); } else { x2 = x; y2 = y; encode(x, y, &code2); } } setlinecolor(WHITE); line(x1, y1, x2, y2); return 0; } int main() { //用户定义a、b坐标 float xa, ya, xb, yb; cout << "please input the coordinate of A point:" << endl; cin >> xa >> ya; cout << "please input the coordinate of B point:" << endl; cin >> xb >> yb; int x0, y0, x1, y1; //0->left bottom; 1->right top; //图形界面 initgraph(640, 480); ExMessage m; //勾勒AB线段:绿色 setlinecolor(GREEN); line(xa, ya, xb, yb); while (true) { m = getmessage(EX_MOUSE | EX_KEY); switch (m.message) { case WM_LBUTTONDOWN: x0 = m.x; y0 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); case WM_RBUTTONDOWN: x1 = m.x; y1 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); //判断用户是左上~右下 / 左下~右上 / 右上~左下 / 右下~左上 if ((x0 < x1) && (y0 > y1)) { XL = x0; XR = x1; YB = y1; YT = y0; } else if ((x0 < x1) && (y0 < y1)) { XL = x0; XR = x1; YB = y0; YT = y1; } else if ((x0 > x1) && (y0 > y1)) { XL = x1; XR = x0; YB = y1; YT = y0; } else if ((x0 > x1) && (y0 < y1)) { XL = x1; XR = x0; YB = y0; YT = y1; } //勾勒裁剪框 setlinecolor(RED); line(XL, YT, XR, YT); line(XL, YB, XR, YB); line(XL, YT, XL, YB); line(XR, YT, XR, YB); //裁剪部分为白色 CSLineClip(xa, ya, xb, yb); case WM_KEYDOWN: if (m.vkcode == VK_ESCAPE) return 0; // 按 ESC 键退出程序 } } closegraph(); return 0; } |
| 2题 |
| // // 程序名称:中值裁剪 // 功 能:用中值分割算法实现直线段裁剪 // 编译环境:VS2019,EasyX_20220116 // 最后修改:2022-3-26 // Special Thanks To Gong WH #include <graphics.h> #include <conio.h> #include <iostream> using namespace std; #define LEFT 1 #define RIGHT 2 #define BOTTOM 4 #define TOP 8 int XL, XR, YB, YT; //区域编码 int encode(float x, float y, int* code) { int c = 0; if (x < XL) { c = c | LEFT; } else if (x > XR) { c = c | RIGHT; } if (y < YB) { c = c | BOTTOM;; } else if (y > YT) { c = c | TOP; } *code = c; return 0; } void MidClip(float x1, float y1, float x2, float y2) { int code1, code2; encode(x1, y1, &code1); encode(x2, y2, &code2);
//无法继续二分 if (abs(x1 - x2) + abs(y1 - y2) <= 2) { return; }
//线段完全不可见 if ((code1 & code2) != 0) { return; } //线段完全可见 if ((code1 | code2) == 0) { setlinecolor(WHITE); line(x1, y1, x2, y2); return; } //线段部分可见=>递归吧。。 int midx = (x1 + x2) / 2, midy = (y1 + y2) / 2;
MidClip(midx, midy, x2, y2); MidClip(x1, y1, midx, midy); /* //这个优化,不大行 int midcode; encode(midx, midy, &midcode); //中点可见,继续二分 if (midcode == 0) { MidClip(midx, midy, x2, y2); MidClip(x1, y1, midx, midy); } //中点不可见,判断中点和哪个点在同一区域 else { int cnt1[4] = { 0 }, cnt2[4] = { 0 }, cntmid[4] = { 0 }; //handle midcode do { if (midcode >= 8) { cntmid[0] = 1; midcode -= 8; } else if (midcode >= 4) { cntmid[1] = 1; midcode -= 4; } else if (midcode >= 2) { cntmid[2] = 1; midcode -= 2; } else if (midcode >= 1) { cntmid[3] = 1; midcode -= 1; } else { continue; } } while (midcode != 0); //handle code1 do { if (code1 >= 8) { cnt1[0] = 1; code1 -= 8; } else if (code1 >= 4) { cnt1[1] = 1; code1 -= 4; } else if (code1 >= 2) { cnt1[2] = 1; code1 -= 2; } else if (code1 >= 1) { cnt1[3] = 1; code1 -= 1; } else { continue; } } while (code1 != 0); //handle code2 do { if (code2 >= 8) { cnt2[0] = 1; code2 -= 8; } else if (code2 >= 4) { cnt2[1] = 1; code2 -= 4; } else if (code2 >= 2) { cnt2[2] = 1; code2 -= 2; } else if (code2 >= 1) { cnt2[3] = 1; code2 -= 1; } else { continue; } } while (code2 != 0); int count1 = 0, count2 = 0; for (int i = 0; i < 4; i++) { if (cnt1[i] == cntmid[i]) { count1++; } if (cnt2[i] == cntmid[i]) { count2++; } } if (count1 > count2) { //point 1 area is closer to midpoint area MidClip(x1, y1, midx, midy); } else { //point 2 area is closer to midpoint area MidClip(midx, midy, x2, y2); } } */ } int main() { //用户定义a、b坐标 int xa, ya, xb, yb; cout << "please input the coordinate of A point:" << endl; cin >> xa >> ya; cout << "please input the coordinate of B point:" << endl; cin >> xb >> yb; int x0, y0, x1, y1; //0->left bottom; 1->right top; //图形界面 initgraph(640, 480); ExMessage m; //勾勒AB线段:绿色 setlinecolor(GREEN); line(xa, ya, xb, yb); while (true) { m = getmessage(EX_MOUSE | EX_KEY); switch (m.message) { case WM_LBUTTONDOWN: x0 = m.x; y0 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); case WM_RBUTTONDOWN: x1 = m.x; y1 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); //判断用户是左上~右下 / 左下~右上 / 右上~左下 / 右下~左上 if ((x0 < x1) && (y0 > y1)) { XL = x0; XR = x1; YB = y1; YT = y0; } else if ((x0 < x1) && (y0 < y1)) { XL = x0; XR = x1; YB = y0; YT = y1; } else if ((x0 > x1) && (y0 > y1)) { XL = x1; XR = x0; YB = y1; YT = y0; } else if ((x0 > x1) && (y0 < y1)) { XL = x1; XR = x0; YB = y0; YT = y1; } //勾勒裁剪框 setlinecolor(RED); line(XL, YT, XR, YT); line(XL, YB, XR, YB); line(XL, YT, XL, YB); line(XR, YT, XR, YB); //裁剪部分为白色 MidClip(xa, ya, xb, yb); case WM_KEYDOWN: if (m.vkcode == VK_ESCAPE) return 0; // 按 ESC 键退出程序 } } closegraph(); return 0; } |
| 3题 |
| // // 程序名称:LB裁剪 // 功 能:用Liang-Barsky算法实现直线段裁剪 // 编译环境:VS2019,EasyX_20220116 // 最后修改:2022-3-17 #include <graphics.h> #include <conio.h> #include <iostream> using namespace std; float XL, XR, YT, YB; void Displayline(float x1, float y1, float x2, float y2) { setlinecolor(WHITE); line(x1, y1, x2, y2); } void LiangBarsky(float x1, float y1, float x2, float y2, float XL, float XR, float YT, float YB) { float ansx1, ansx2, ansy1, ansy2; //平行于y轴 if (x1 - x2 == 0) { if (x1<XL || x1>XR) { return; } else { int ymin = max(YB, min(y1, y2)); int ymax = min(YT, max(y1, y2)); if (ymin <= ymax) { ansx1 = ansx2 = x1; ansy1 = ymin; ansy2 = ymax; } else { return; } } } //平行于x轴 else if (y1 - y2 == 0) { if (y1<YB || y1>YT) { return; } else { int xmin = max(XL, min(x1, x2)); int xmax = min(XR, max(x1, x2)); if (xmin <= xmax) { ansy1 = ansy2 = y1; ansx1 = xmin; ansx2 = xmax; } else { return; } } } //不平行于坐标轴 else { float p1, p2, p3, p4; float q1, q2, q3, q4; p1 = -(x2 - x1); p2 = -p1; p3 = -(y2 - y1); p4 = -p3; q1 = x1 - XL; q2 = XR - x1; q3 = y1 - YB; q4 = YT - y1; float u1, u2, u3, u4; u1 = q1 / p1; u2 = q2 / p2; u3 = q3 / p3; u4 = q4 / p4; float umin, umax; if (p1 < 0) { if (p3 < 0) { umin = max(0, max(u1, u3)); umax = min(1, min(u2, u4)); } else { umin = max(0, max(u1, u4)); umax = min(1, min(u2, u3)); } } else { if (p3 < 0) { umin = max(0, max(u2, u3)); umax = min(1, min(u1, u4)); } else { umin = max(0, max(u2, u4)); umax = min(1, min(u1, u3)); } } if (umin <= umax) { ansx1 = x1 + umin * (x2 - x1); ansx2 = x1 + umax * (x2 - x1); ansy1 = y1 + umin * (y2 - y1); ansy2 = y1 + umax * (y2 - y1); } else { return; } } Displayline(ansx1, ansy1, ansx2, ansy2); return; } int main() { //用户定义a、b坐标 float xa, ya, xb, yb; cout << "please input the coordinate of A point:" << endl; cin >> xa >> ya; cout << "please input the coordinate of B point:" << endl; cin >> xb >> yb; float x0, y0, x1, y1; //0->left bottom; 1->right top; initgraph(640,480); ExMessage m; //勾勒AB线段:绿色 setlinecolor(GREEN); line(xa, ya, xb, yb); while (true) { m = getmessage(EX_MOUSE | EX_KEY); switch (m.message) { case WM_LBUTTONDOWN: x0 = m.x; y0 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); case WM_RBUTTONDOWN: x1 = m.x; y1 = m.y; setlinecolor(WHITE); setfillcolor(GREEN); fillrectangle(m.x - 3, m.y - 3, m.x + 3, m.y + 3); //判断用户是左上~右下 / 左下~右上 / 右上~左下 / 右下~左上 if ((x0 < x1) && (y0 > y1)) { XL = x0; XR = x1; YB = y1; YT = y0; } else if ((x0 < x1) && (y0 < y1)) { XL = x0; XR = x1; YB = y0; YT = y1; } else if ((x0 > x1) && (y0 > y1)) { XL = x1; XR = x0; YB = y1; YT = y0; } else if ((x0 > x1) && (y0 < y1)) { XL = x1; XR = x0; YB = y0; YT = y1; } //勾勒裁剪框 setlinecolor(RED); line(XL, YT, XR, YT); line(XL, YB, XR, YB); line(XL, YT, XL, YB); line(XR, YT, XR, YB); //裁剪部分为白色 LiangBarsky(xa, ya, xb, yb, XL, XR, YT, YB); case WM_KEYDOWN: if (m.vkcode == VK_ESCAPE) return 0; // 按 ESC 键退出程序 } } closegraph(); //关闭绘图窗口 return 0; } |


























 1242
1242

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










