cweek1
C
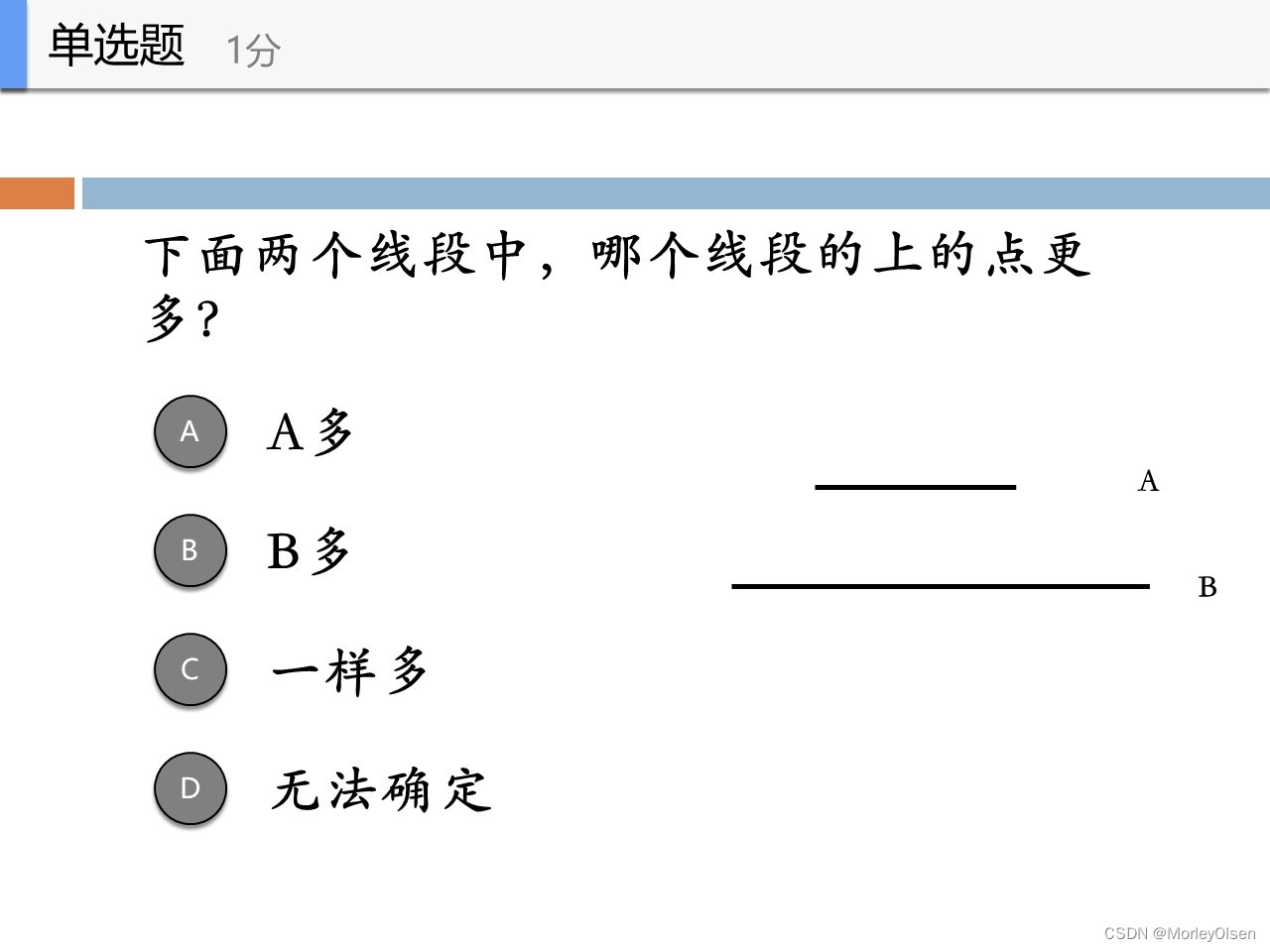
首先将A和B线段位于平行状态
然后连接两个线段的左侧端点和右侧端点,相交于一点
从这点开始,从左向右引出射线,都可以与A、B同时相交于射线上一点
因此A和B是可比的,可比即一样多
C
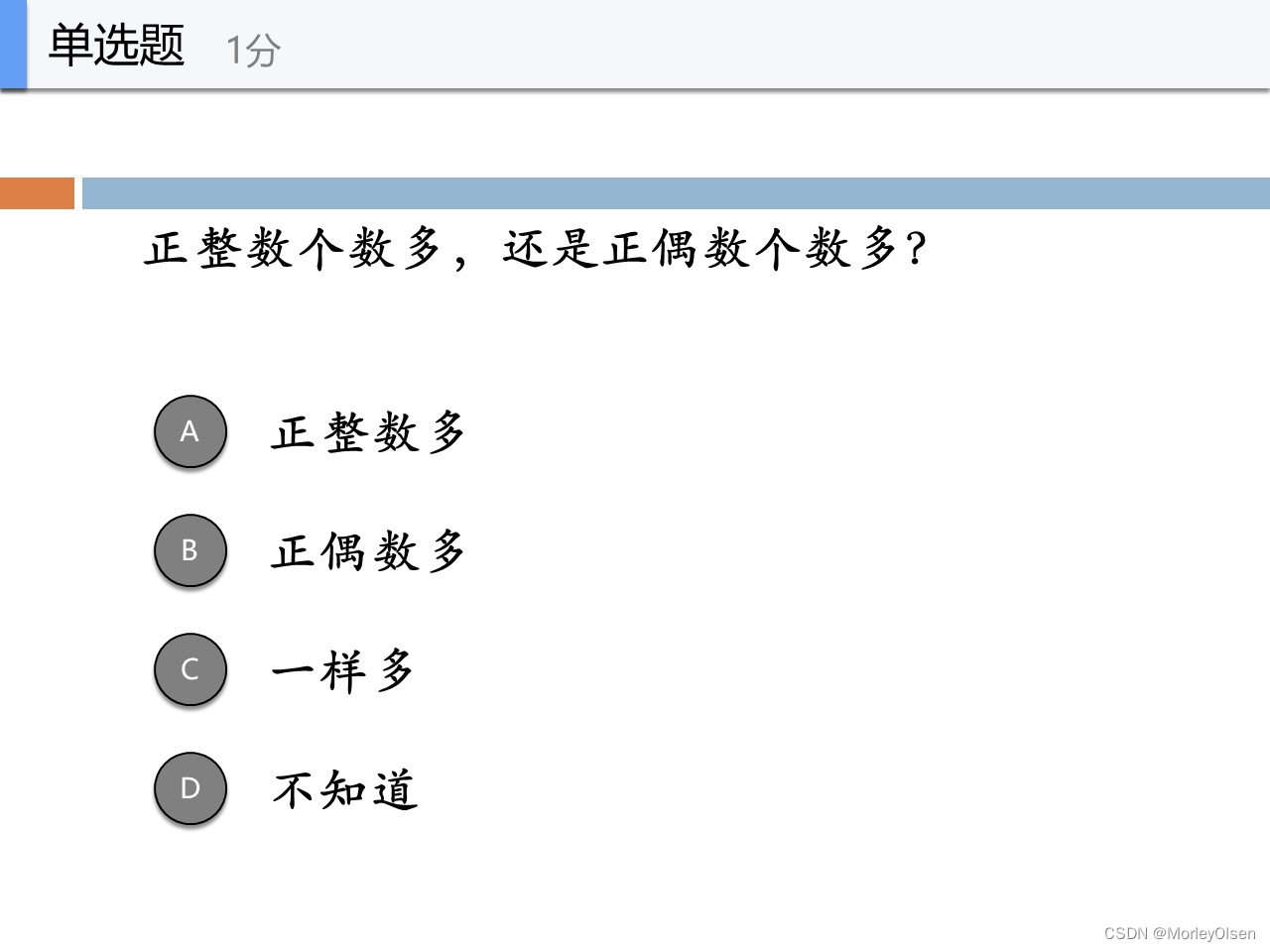
令正整数为x,正偶数为y
则y = 2 * x
可以有上面的一一对应的函数映射关系,因此一样多
C
B
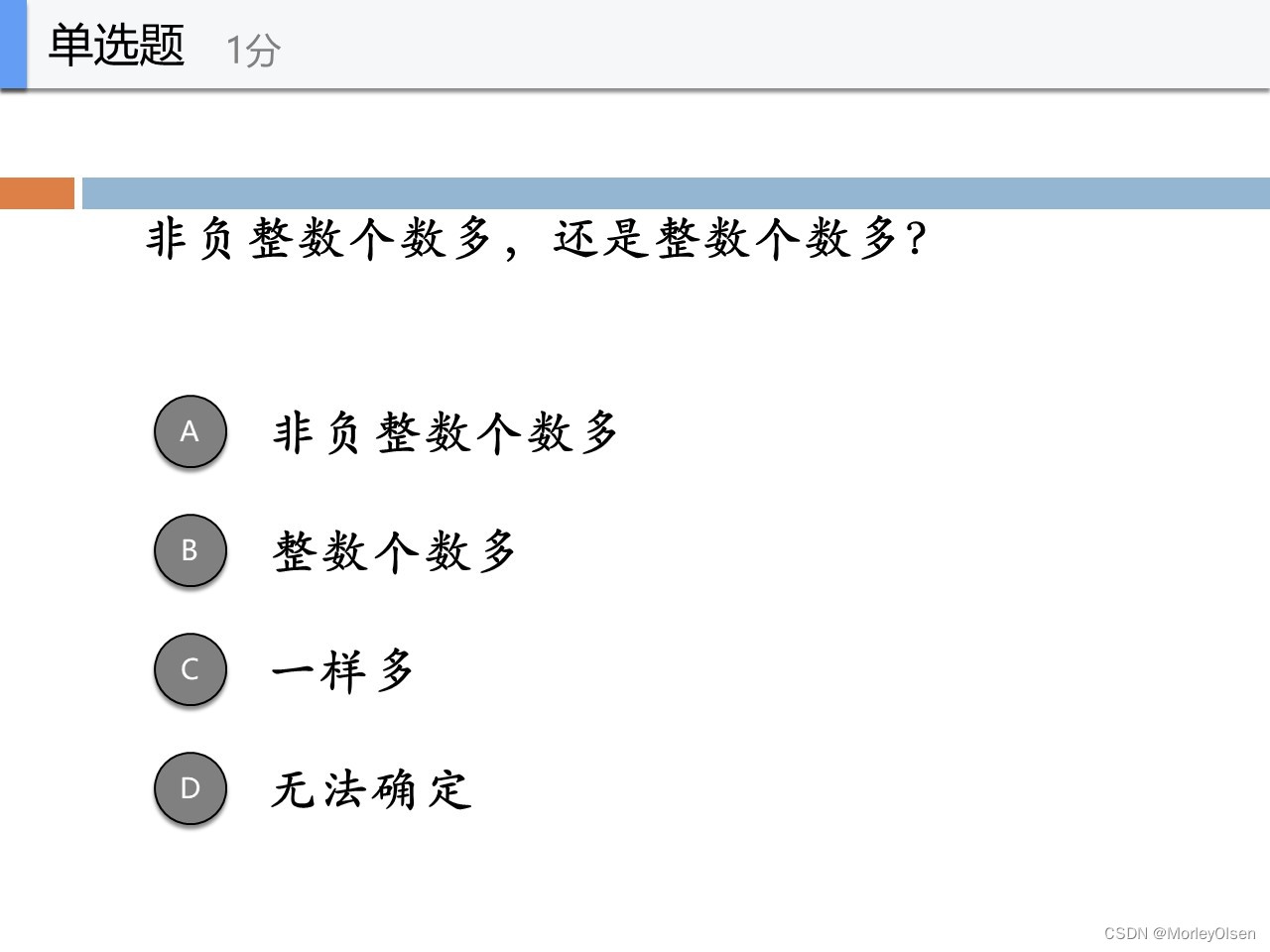
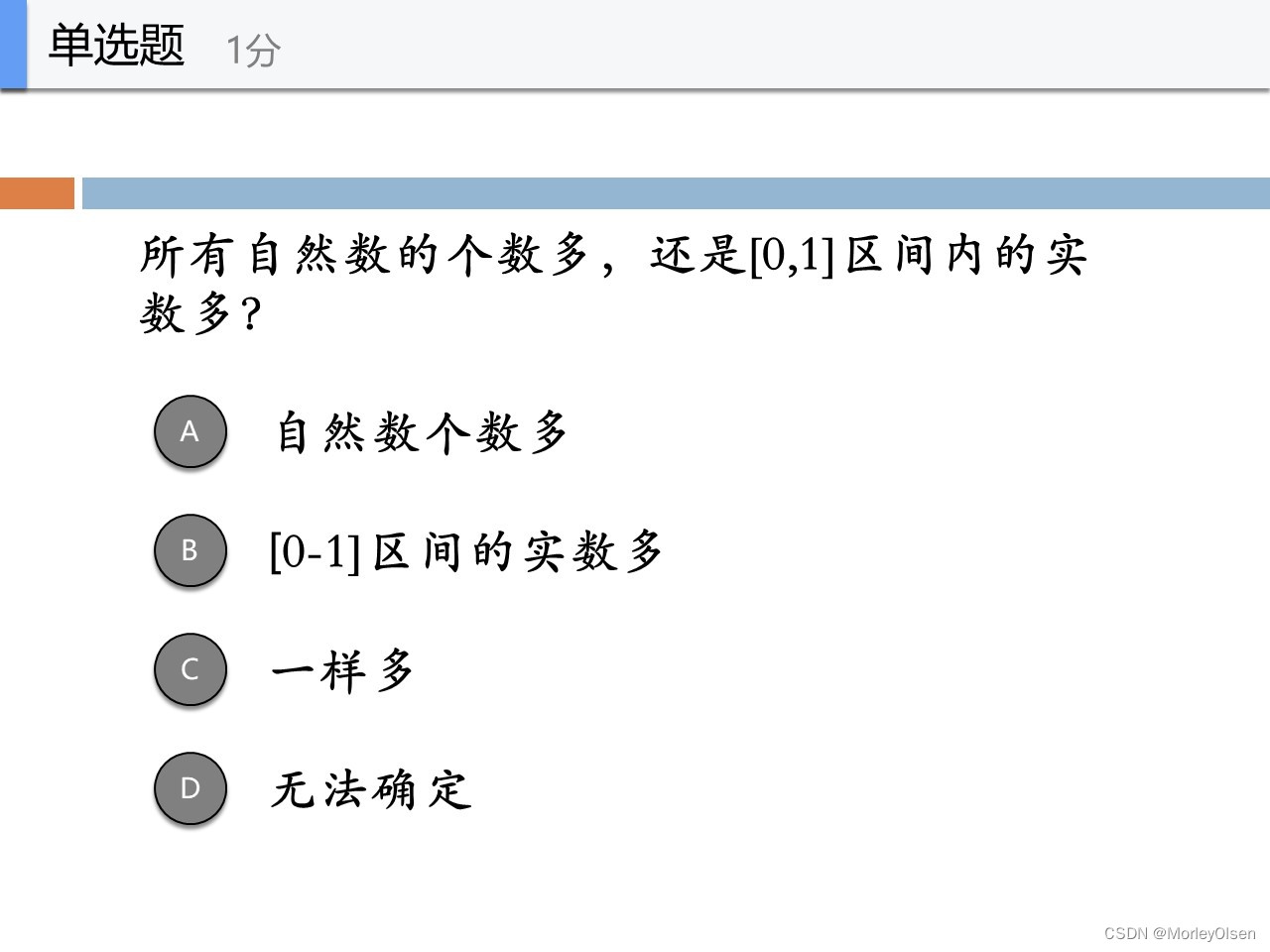
两个相邻自然数之间,不能再有自然数
而两个相邻实数之间,还能再有实数。即实数没有相邻的概念。
因此自然数和区间内实数不是一一对应的,且实数范围更大
C
区间[0,5]可以缩放到[0,12]
此题类似第一个线段的映射
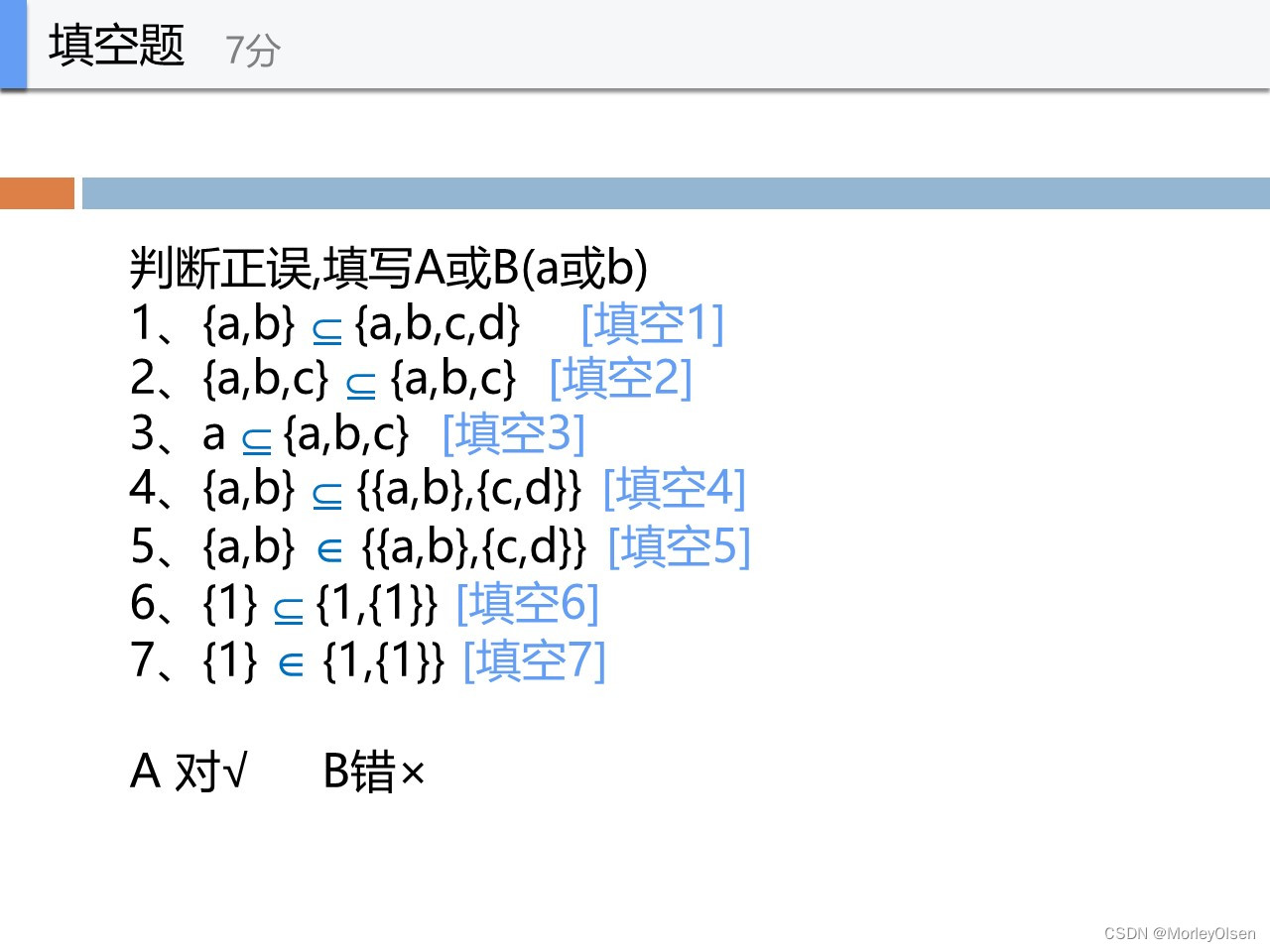
A
A
B,应该是元素的∈
B,应该是元素的∈
A
A
A
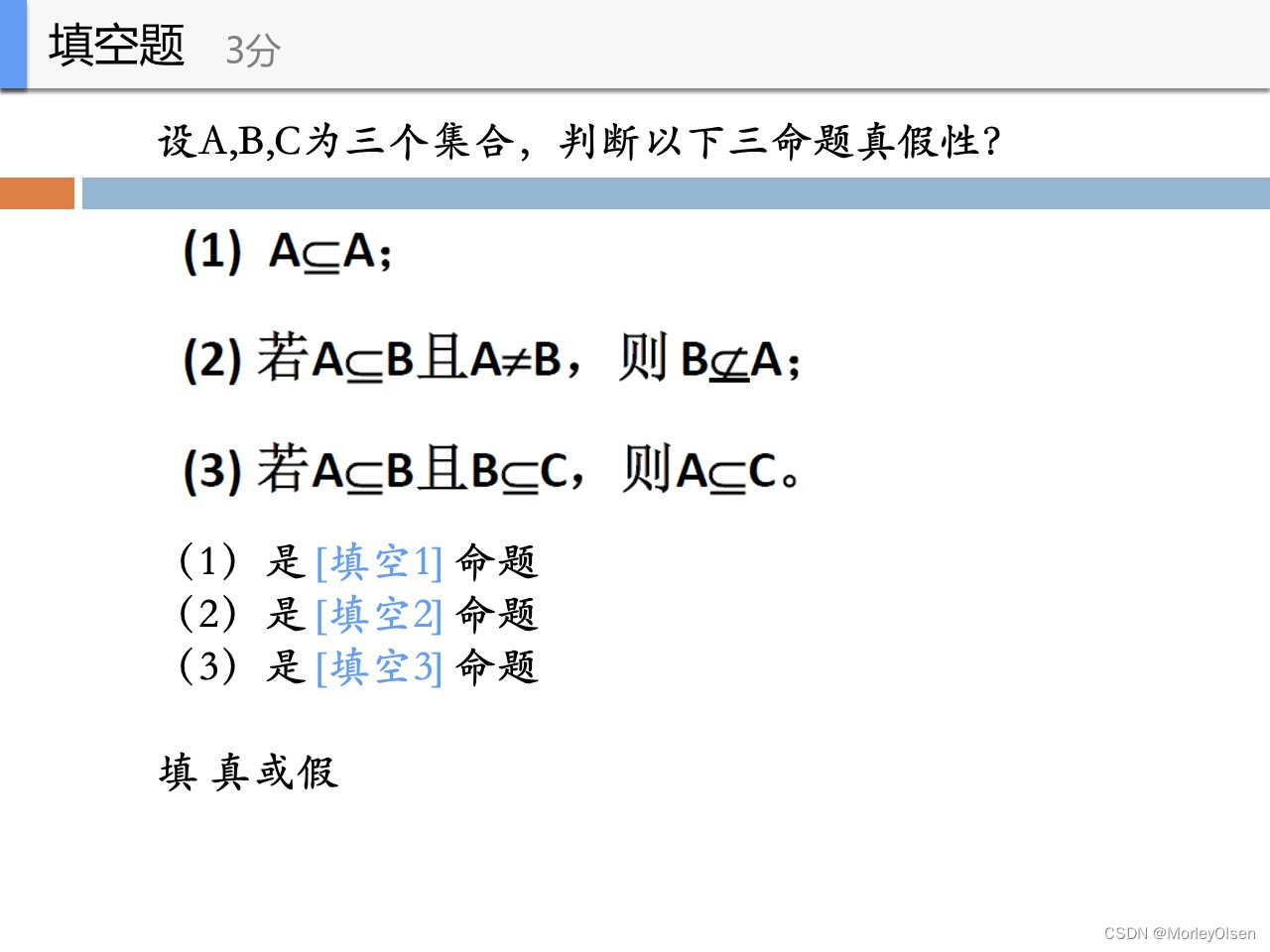
真
真
真
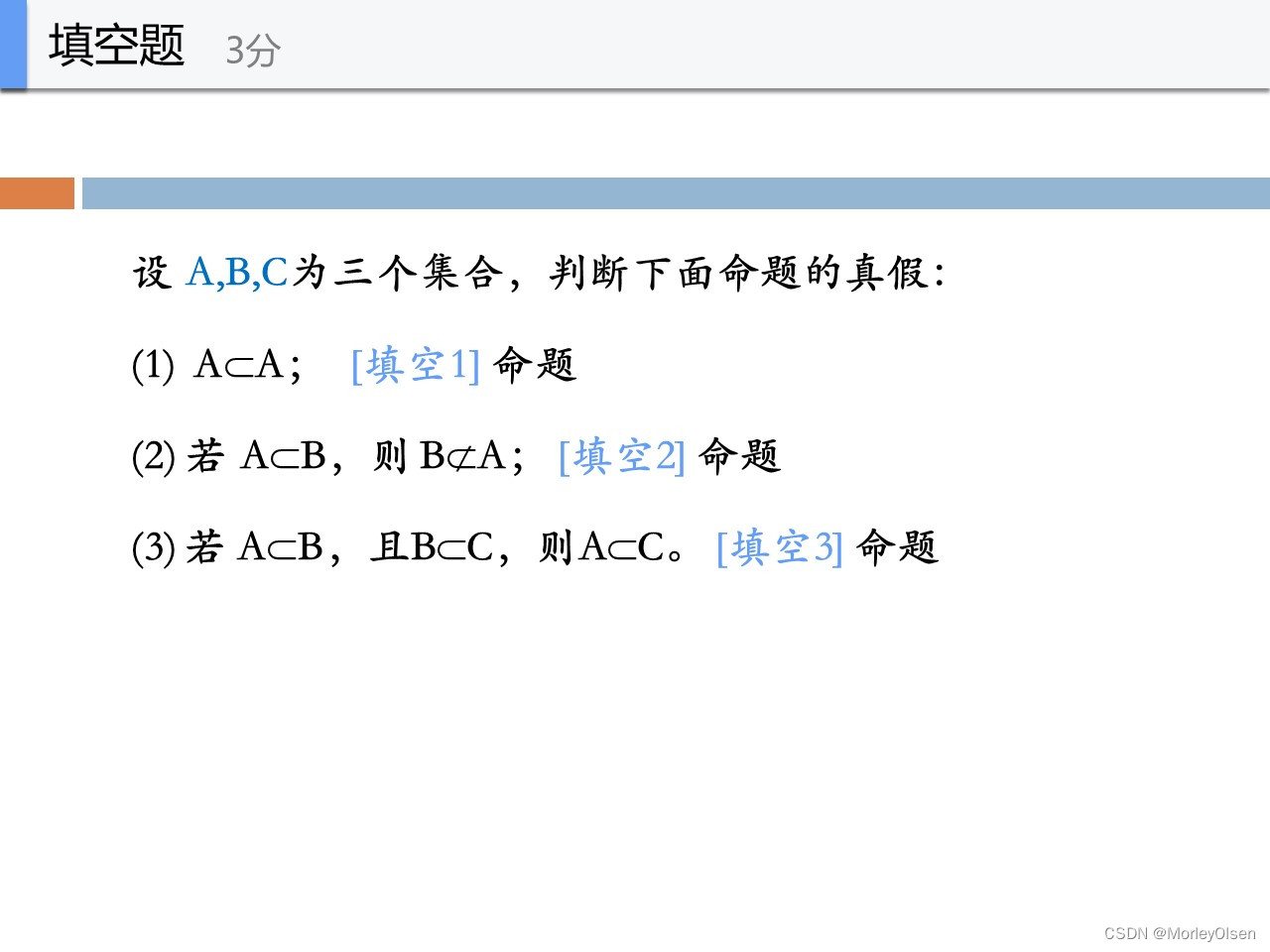
假,真子集不包含本身
真
真
week2
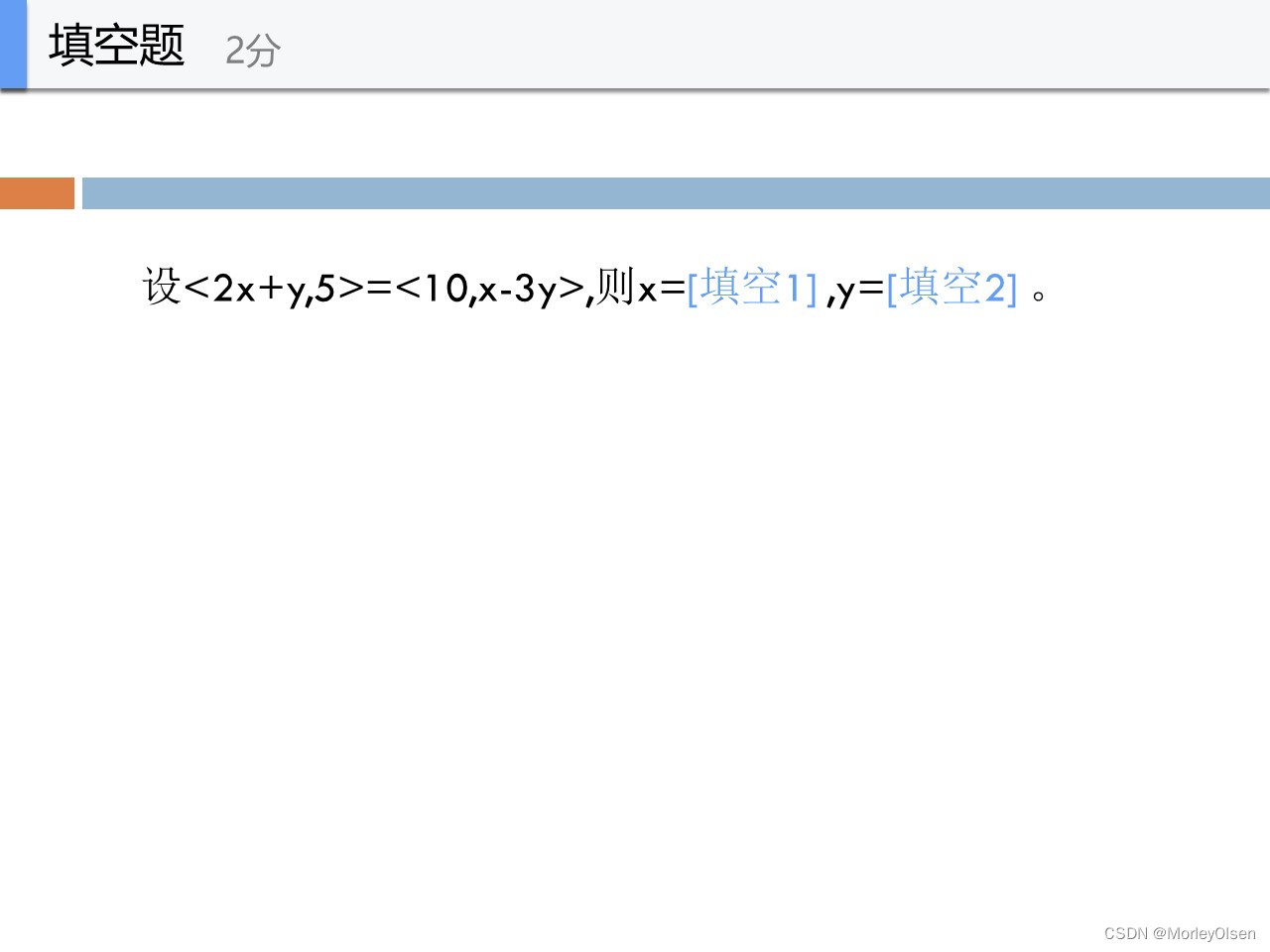
可列出方程组
2x+y=10
x-3y=5
求解可得
x=5
y=0

A
P(A)的元素个数为2^n
A的元素个数为n
因此P(A)和A的笛卡尔积的元素个数为2^n * n
因为序列中的第一个位置的元素由P(A)提供,可提供2^n个
序列中的第二个位置的元素由A提供,可提供n个
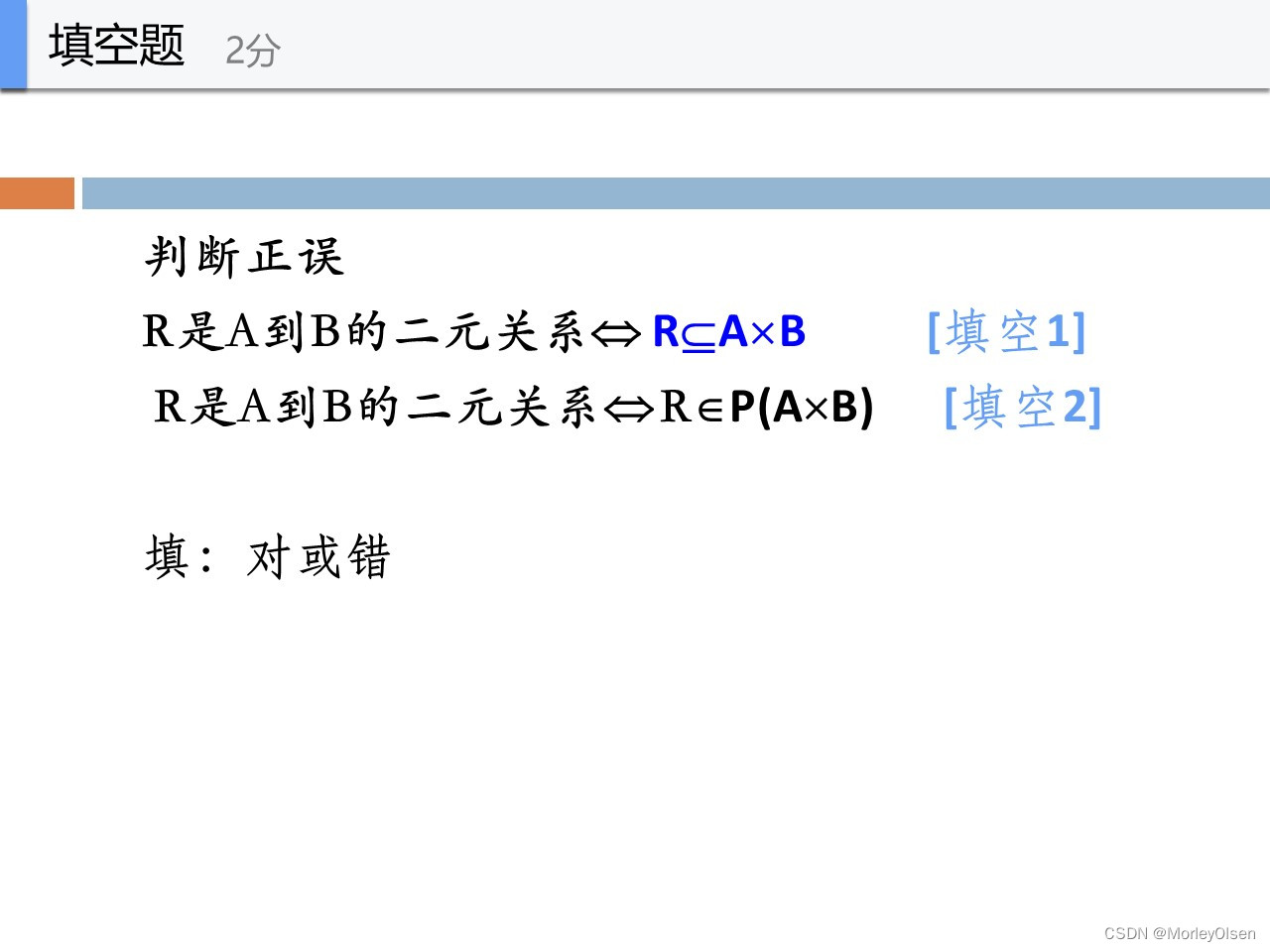
【1】对
如果R是A到B的二元关系,那么R中的元素,第一个位置来自A,第二个位置来自B
因此,R一定包含于A和B的笛卡尔积
【2】对
同理,R中的元素,第一个位置来自A,第二个位置来自B
因此,R一定属于A和B的笛卡尔积的幂集
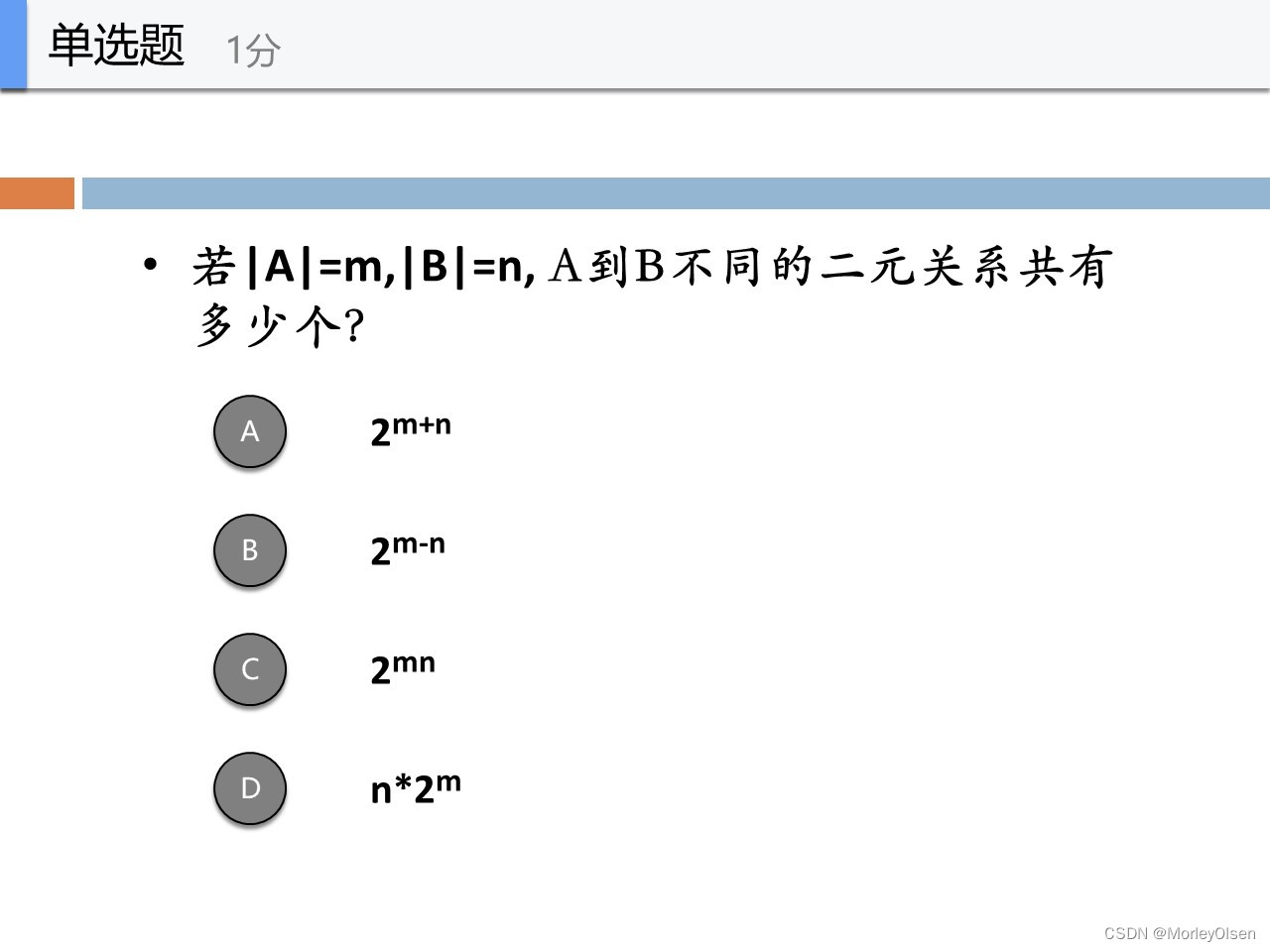
C
A和B的笛卡尔积的个数有m*n个
因此A到B不同的二元关系有2^(mn)个
因为A和B的笛卡尔积的幂集就是A到B的二元关系
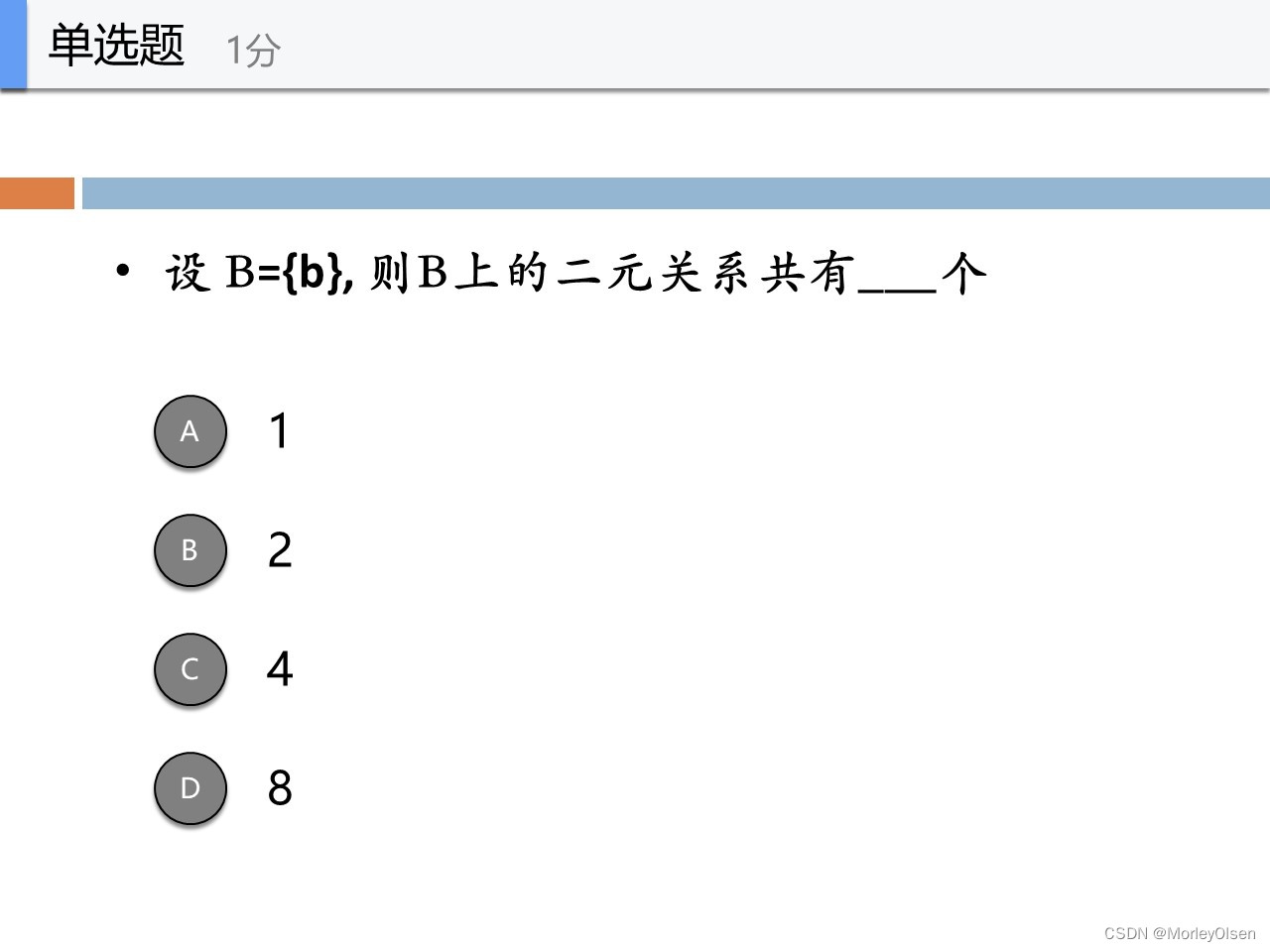
B中的笛卡尔积个数是1,即<b,b>
因此 B上的二元关系有2^1=2个
week3 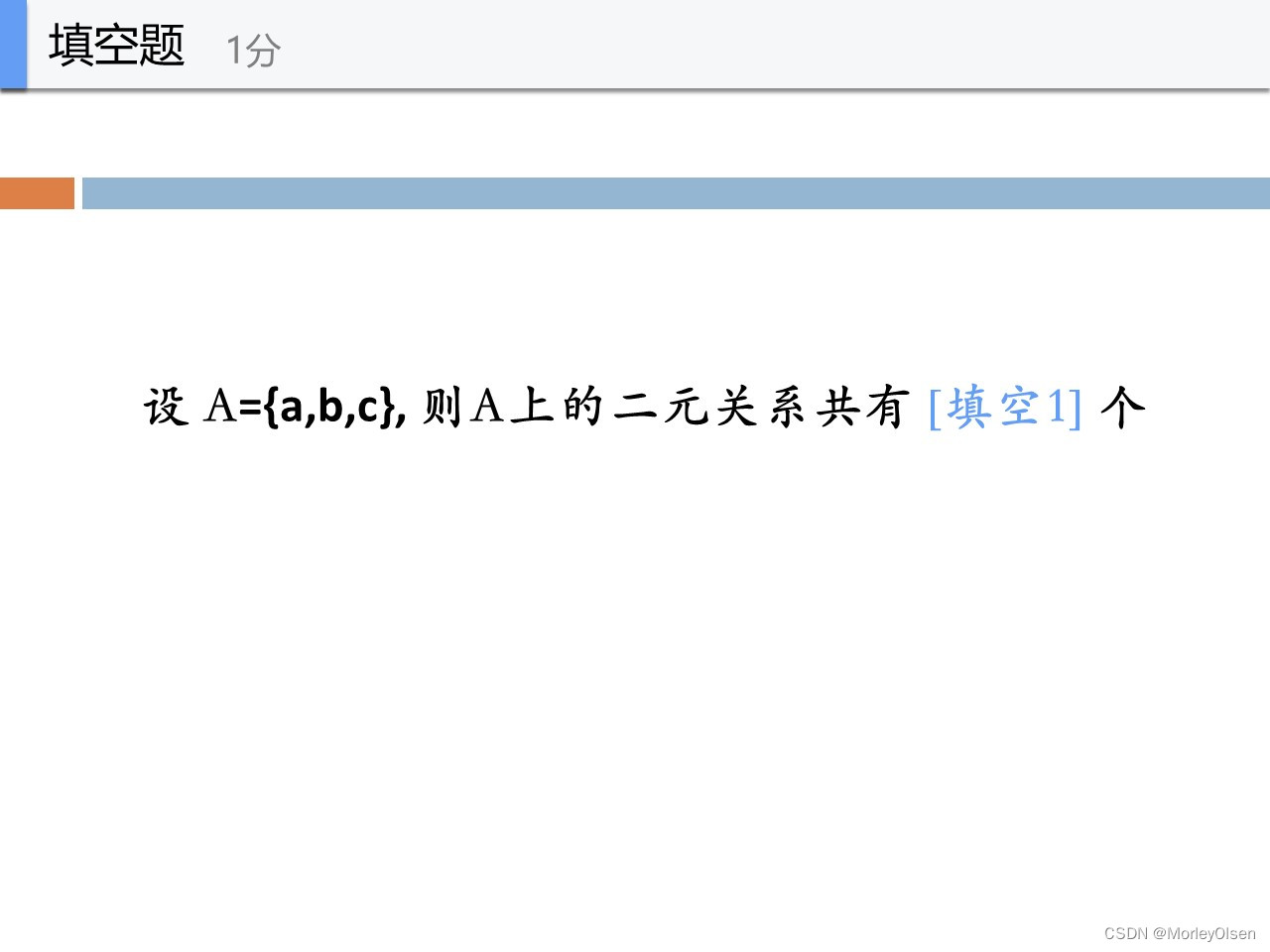
因此A的笛卡尔积的个数是9个
A上的二元关系是2^9=512个

D
B
A
D
画图即可解决这道题,如下图所示
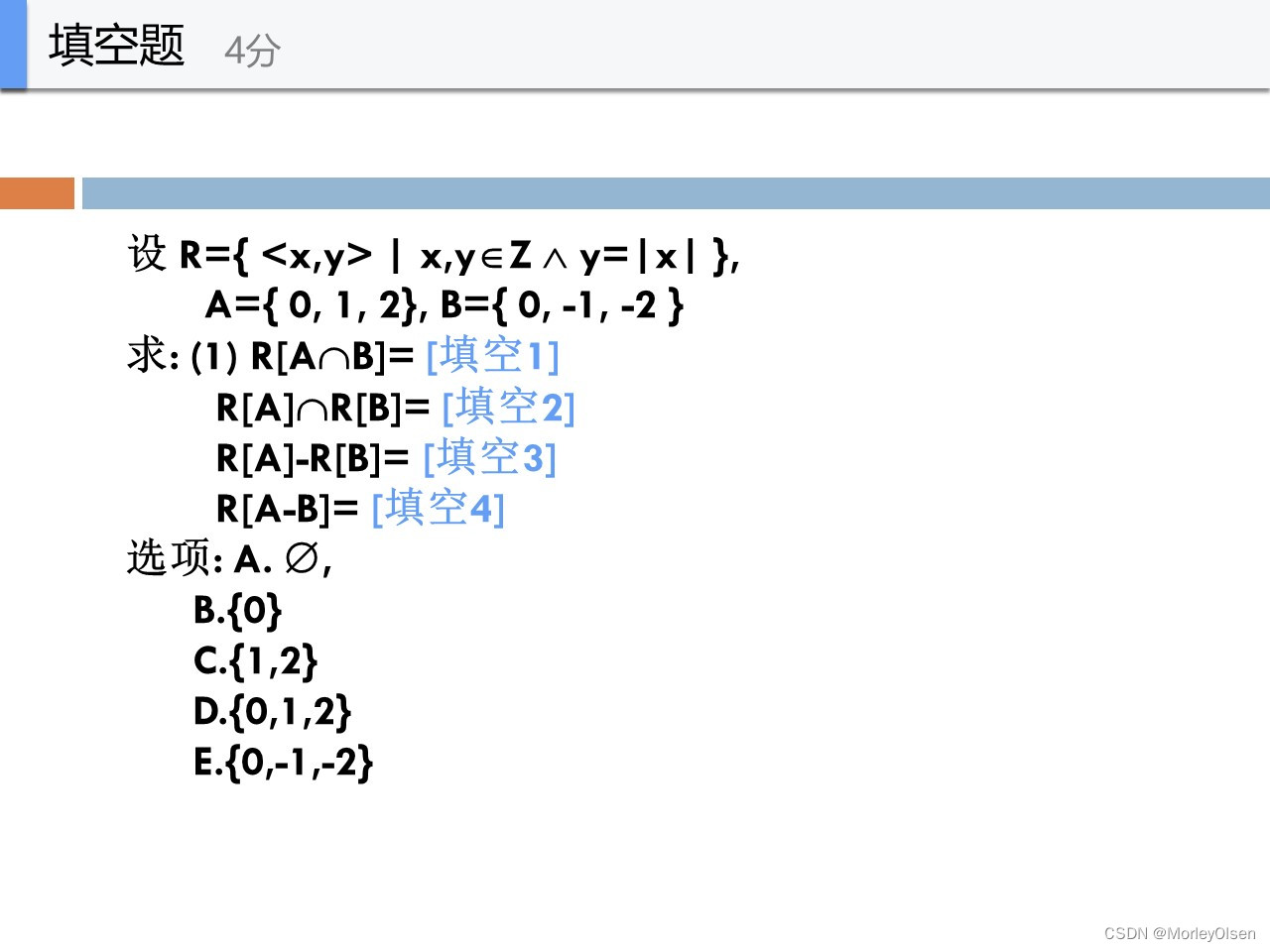
B
D
A
C
首先R[x]的结果是<x,y>中的y
第一题:
A∩B={ 0 }
因此R[0] = { <0,0> } = 0
第二题:
R[A] = { <0,0> <1,1> <2,2> } = { 0, 1, 2 }
R[B] = { <0,0> <-1,1> <-2,2> } = { 0, 1, 2 }
因此结果是{ 0, 1, 2 }
第三题:
结果是空集
第四题:
A - B = {1,2}
R[A - B] = { <1,1> <2,2> } = { 1, 2 }

week4
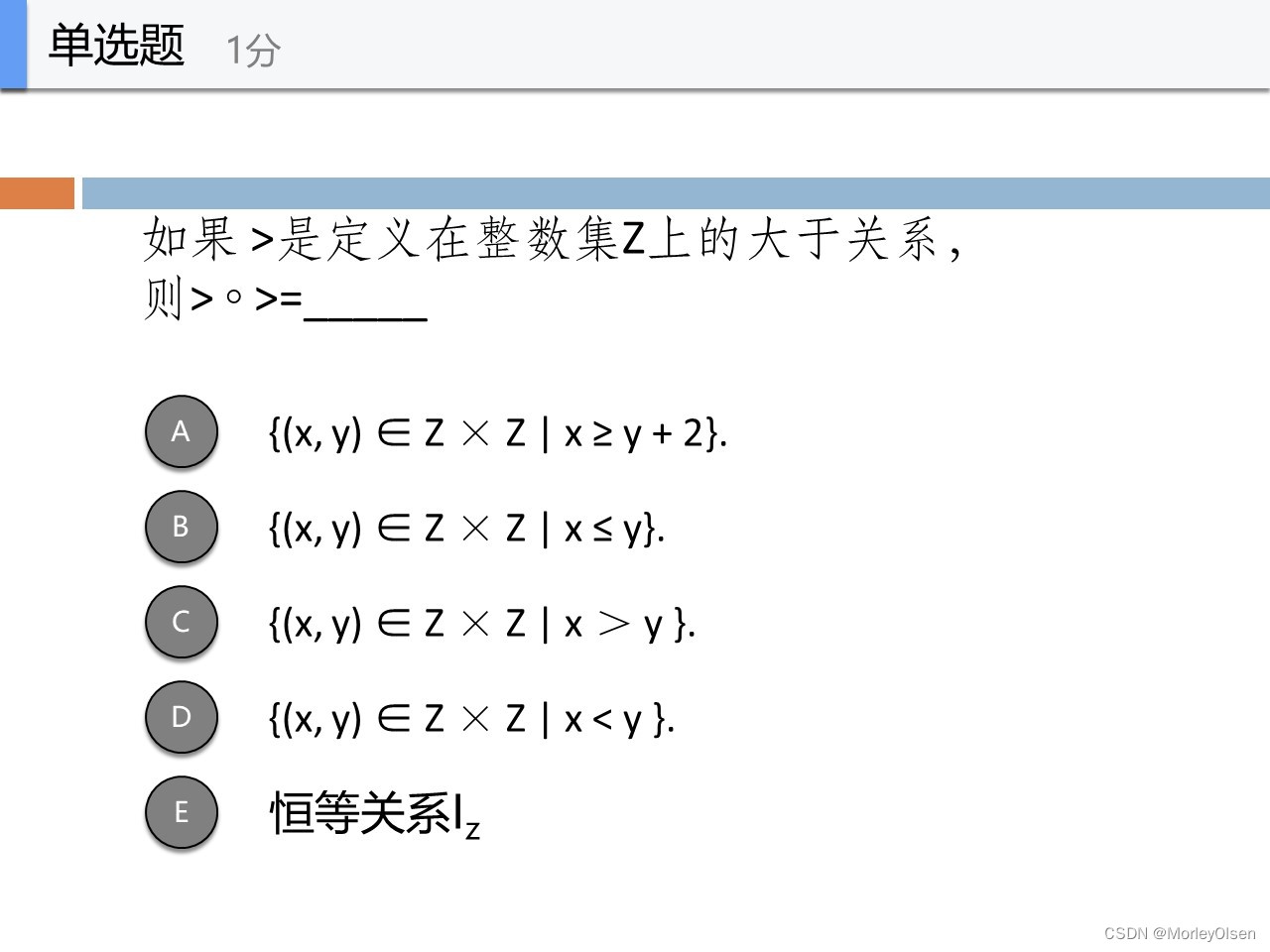
A
假设我们选取关系<1,0>
那么从0开始,可以合成的关系有<0,-1> <0,-2> ...
所以合成的结果有<1,-1> <1,-2>...
可以观察到,x和y最小相差2,即满足x>=y+2
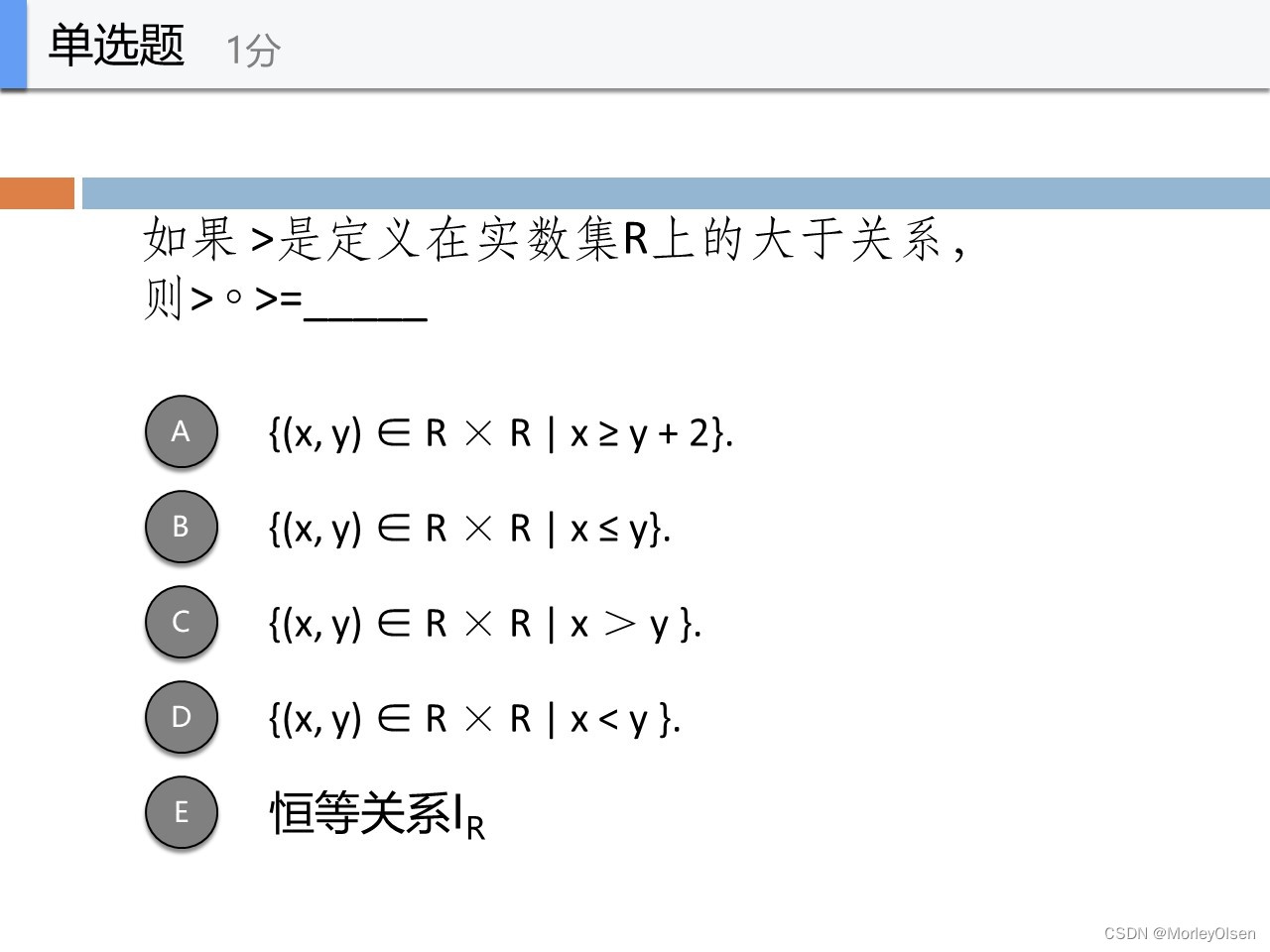
C
因为此处的数据范围是实数集合R
则可以得到:<x, x-无穷小> < x-无穷小, x-无穷小-无穷小> 可以合成为<x,x-无穷小-无穷小>
因此x>y
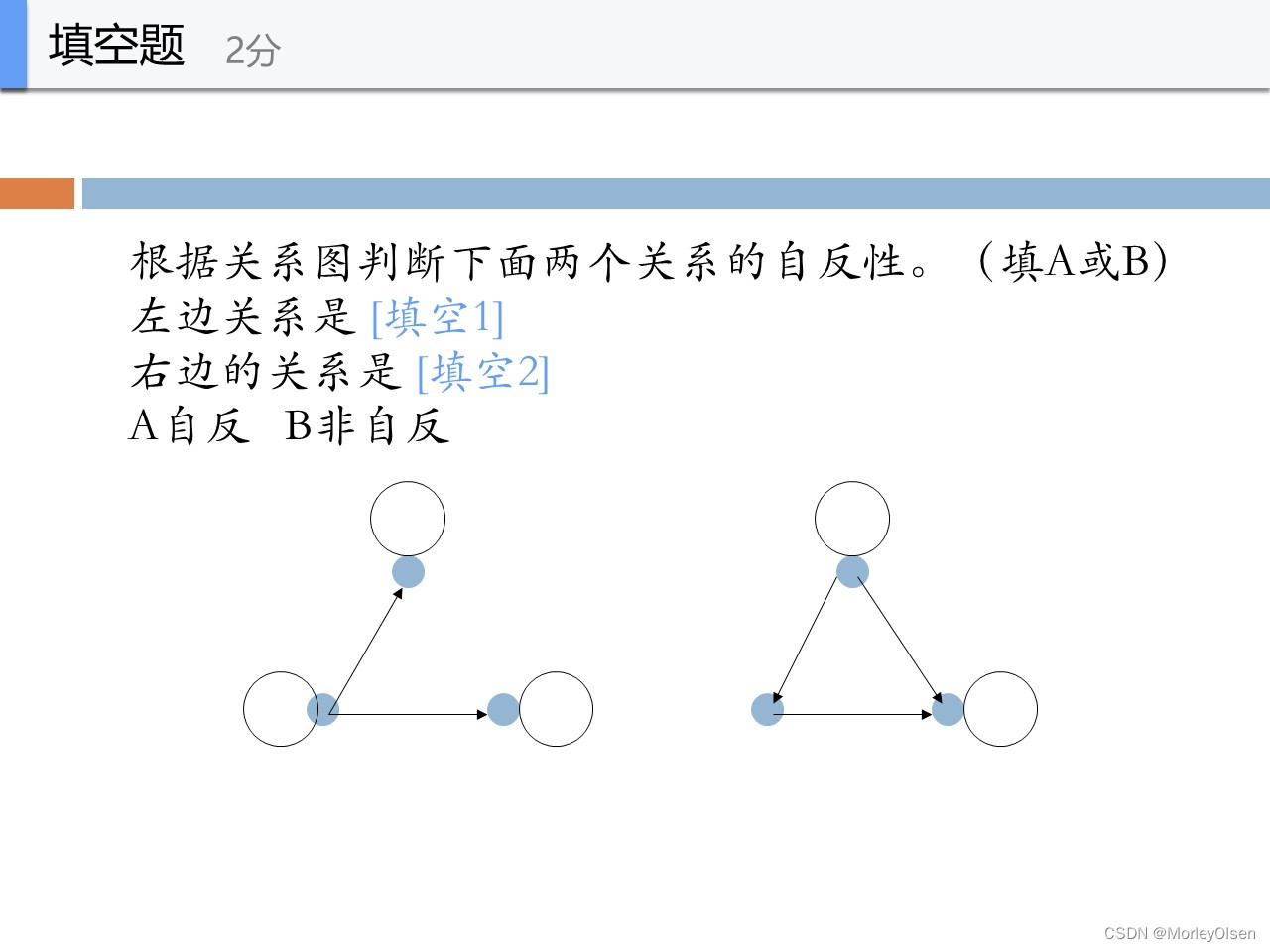
A、B
左图每个node都有自环,因此是自反的
右图部分node有自环,因此是非自反的
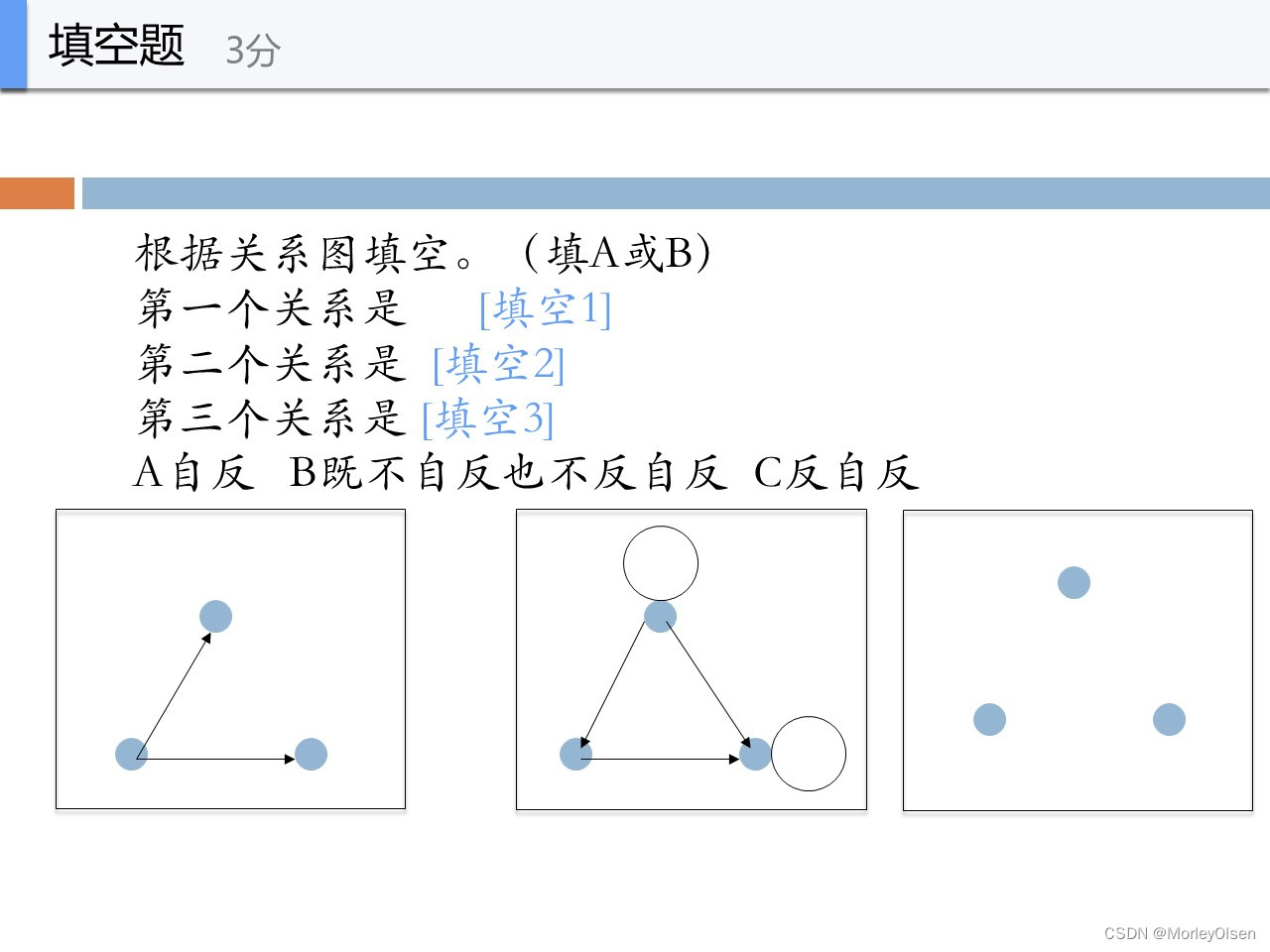
CBC
第一个图,满足0个自环,因此是反自反
第二个图,有2个自环,且有结点没有自环,因此既不是自反也不是反自反
第三个图,满足0个自环,因此是反自反
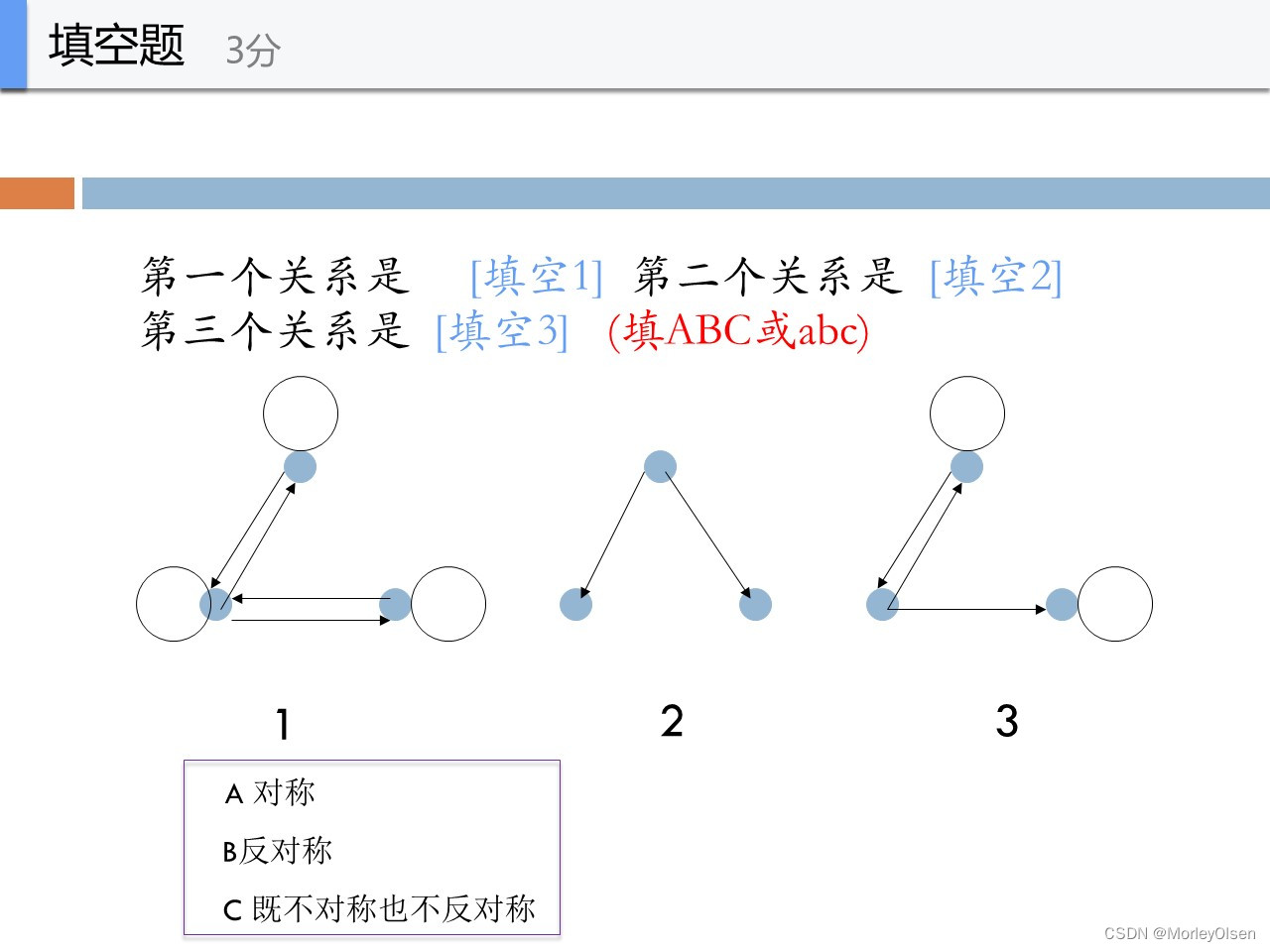
ABC
第一个图,满足无单向边,因此是对称
第二个图,满足无双向边,因此是反对称
第三个图,既有单向边又有双向边,因此不对称且不反对称
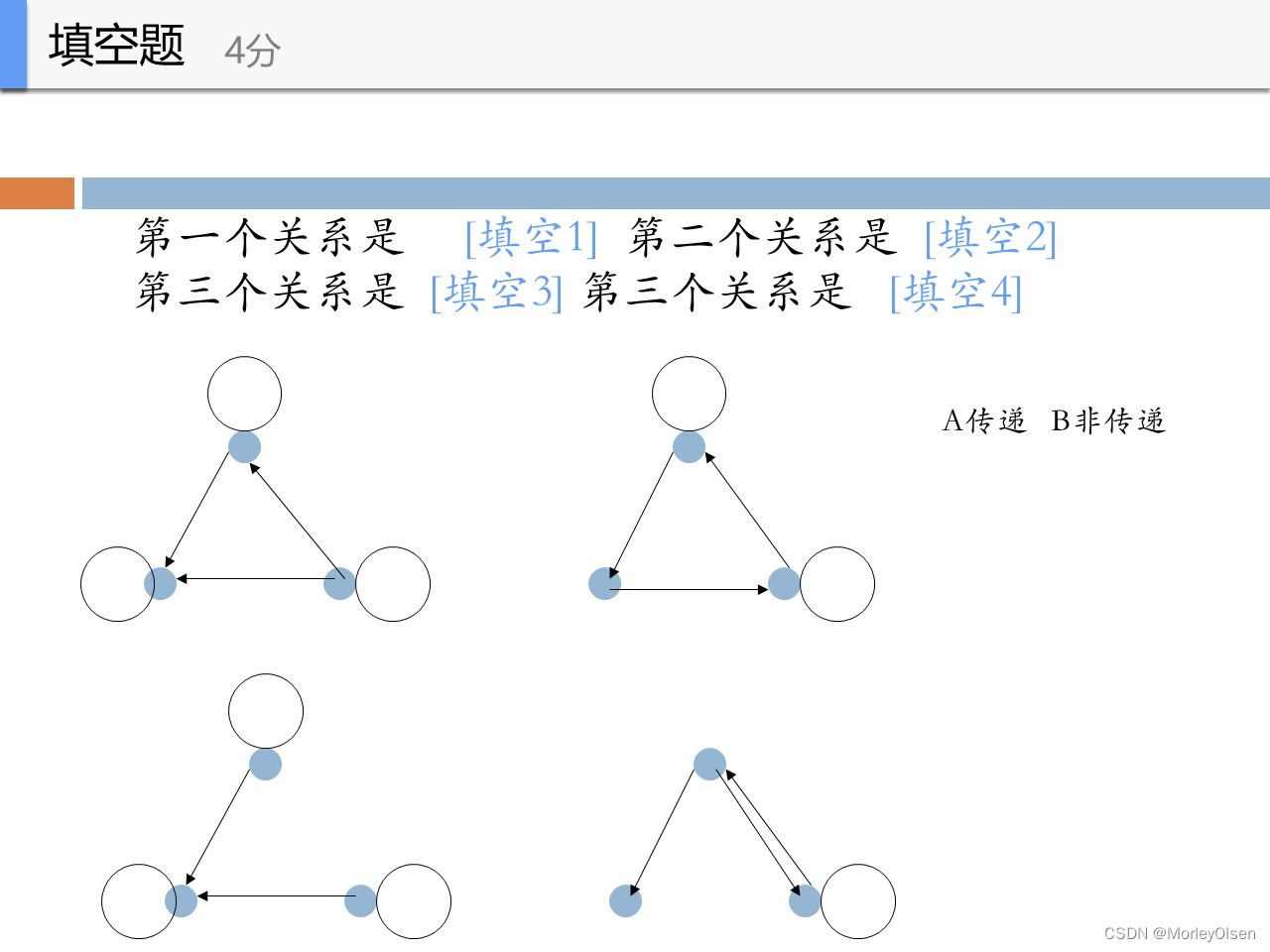
ABAB
首先明确传递的概念,若图中有<a,b>和<b,c>,则一定有<a,c>
通过遍历每个顶点的所有出边,即可判断
我们假设每个node的名字如下:上面是a,左侧是b,右侧是c。
第一个图,显然满足传递
第二个图,<c,a>和<a,b>存在,但是<c,b>不存在,因此非传递
第三个图,显然满足传递
第四个图,<a,c>和<c,a>存在,但是<a,a>不存在,因此非传递
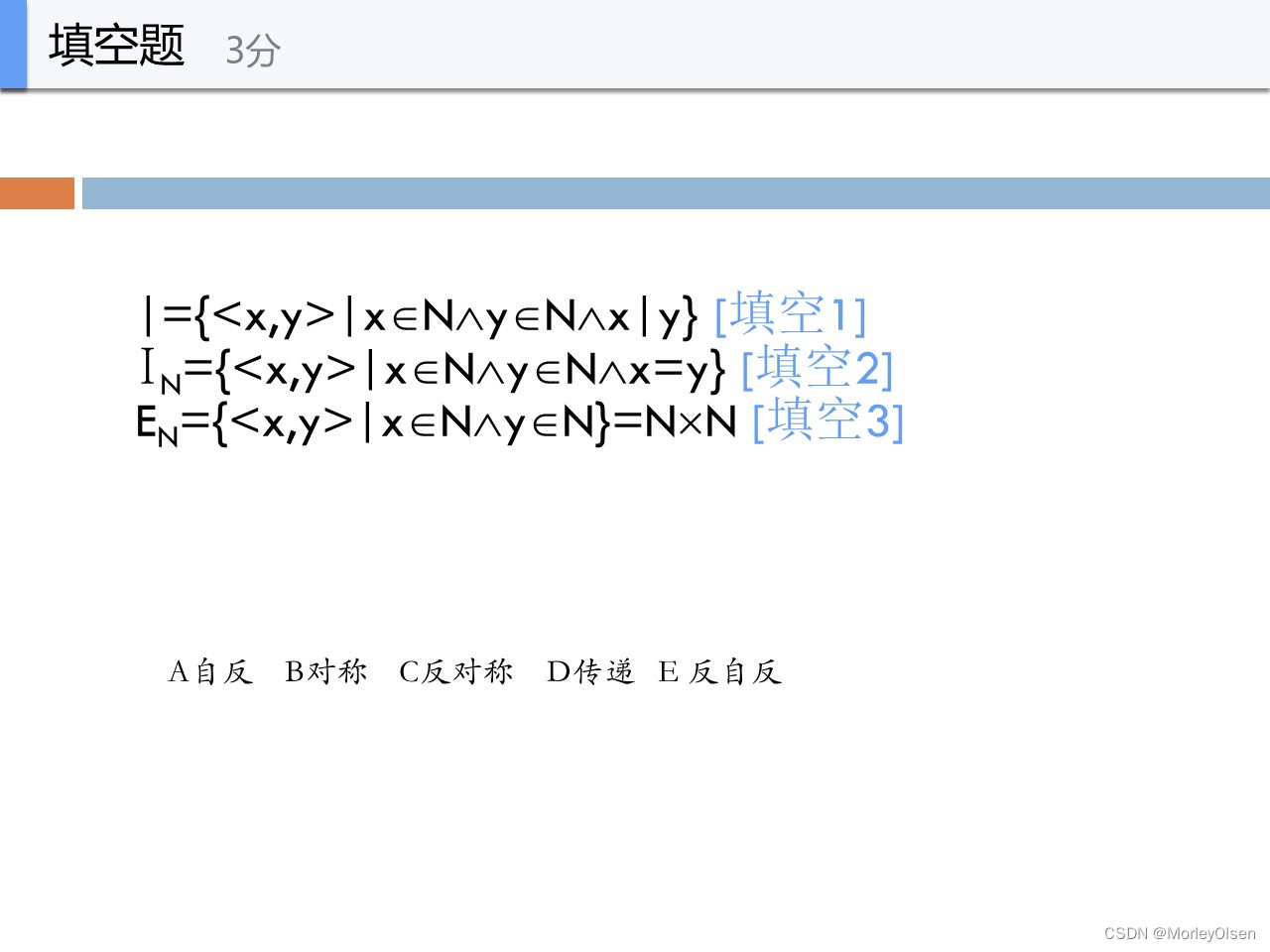
CD
ABCD
ABD
易错点:对于第一个关系,由于0不能整除0(0不能是分母),因此不满足自反性
其他均可以按照性质定义进行推导,此处不再赘述
week5
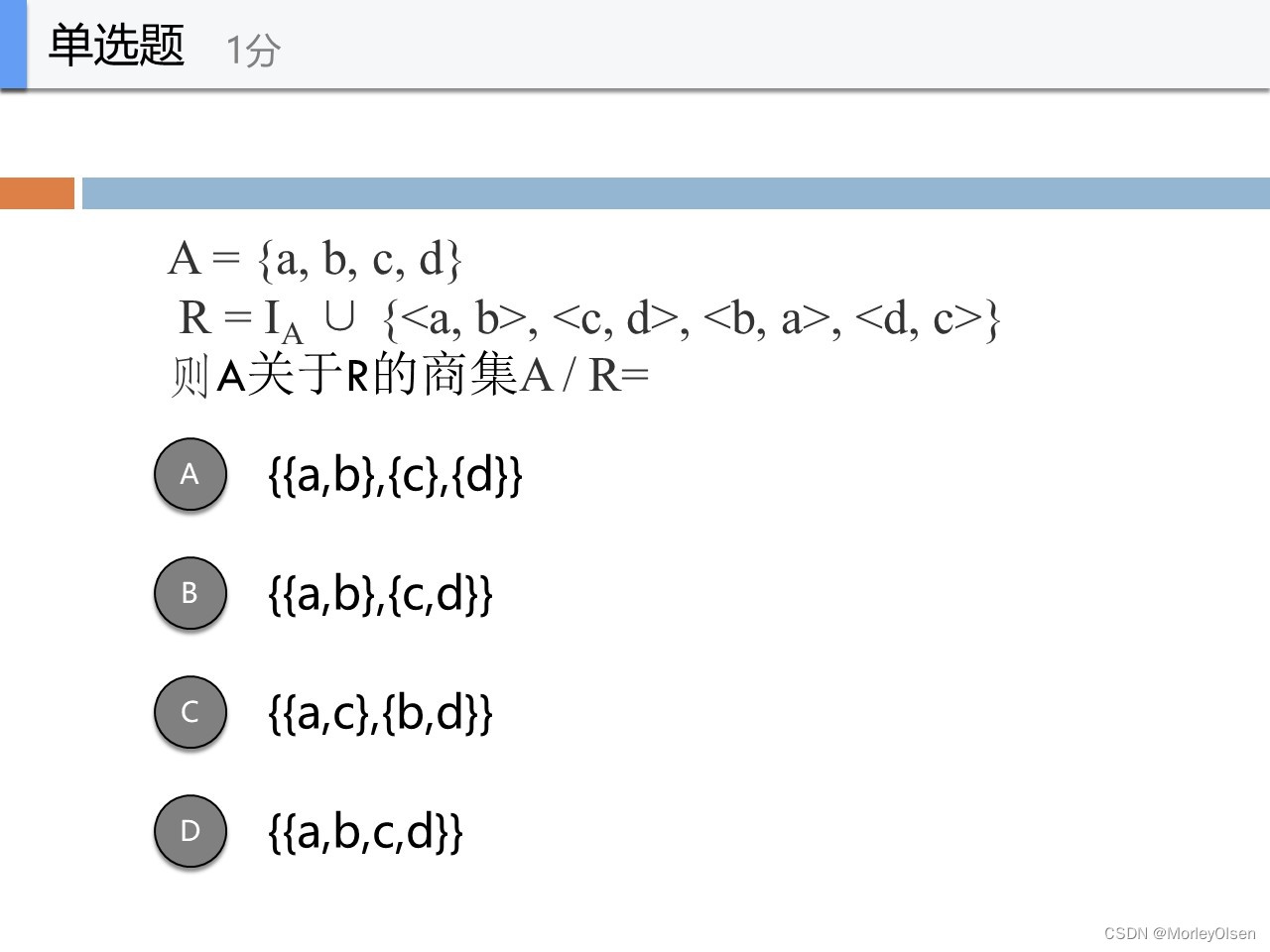
B
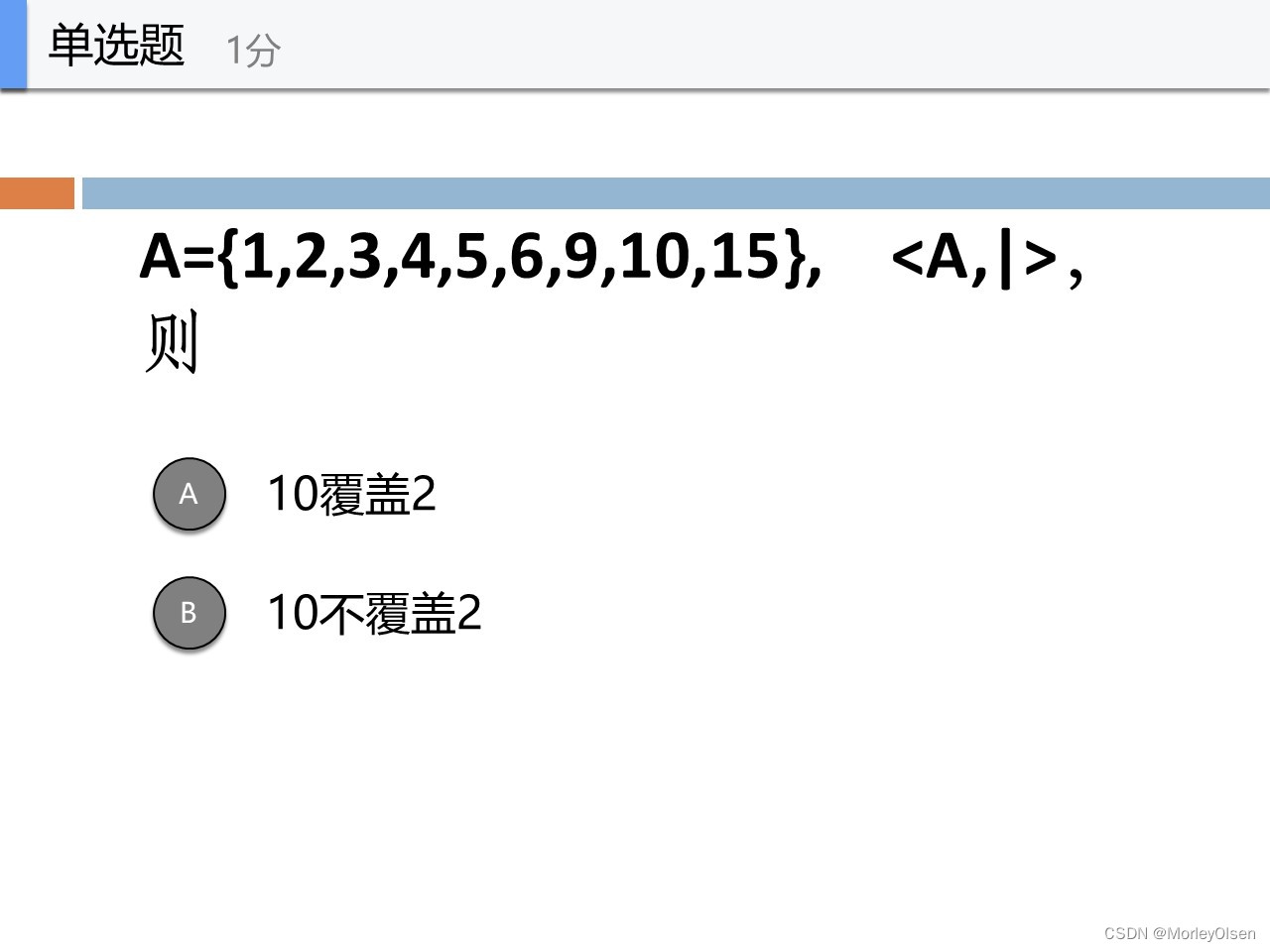
A
week6
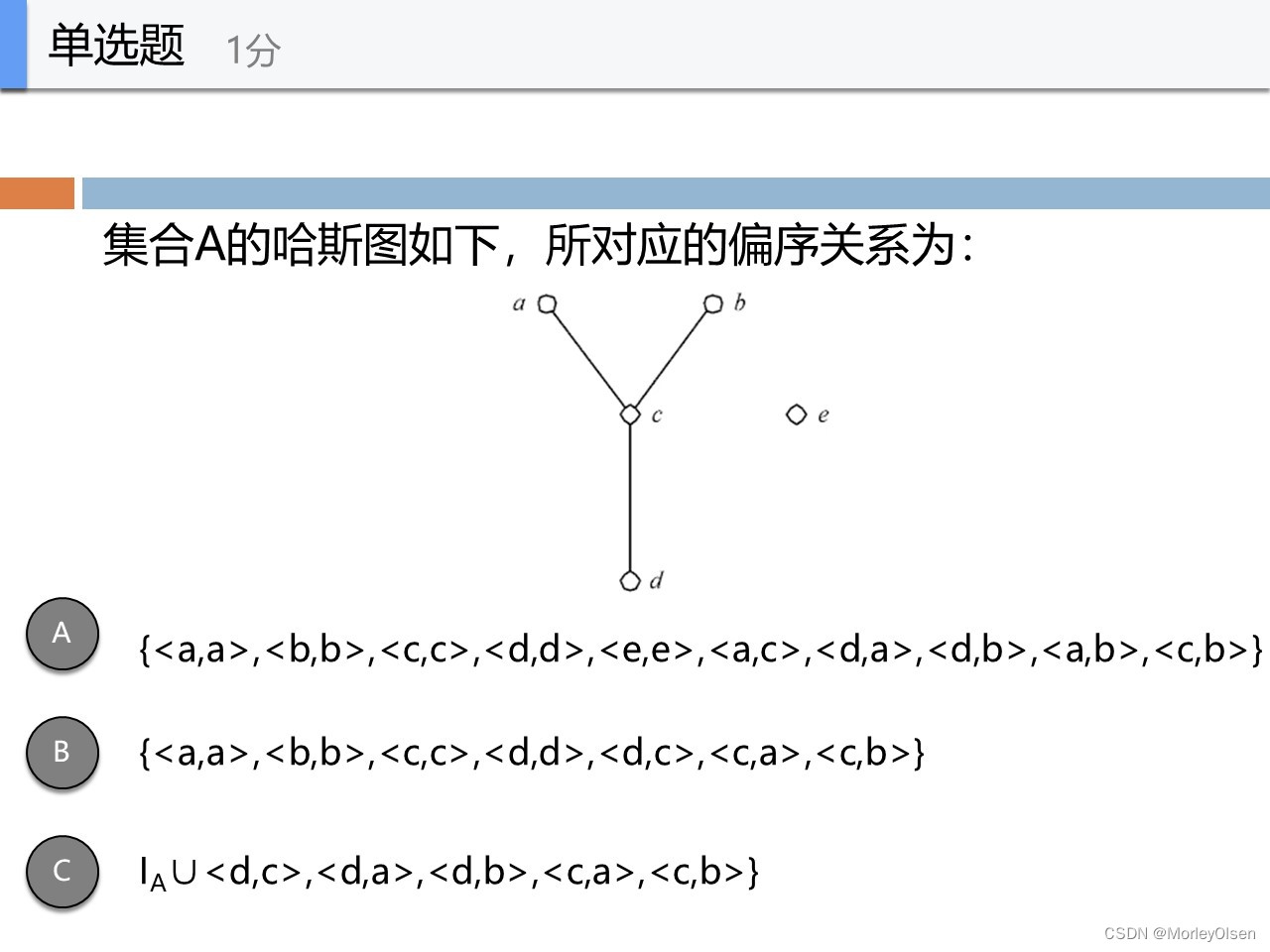
C
首先偏序关系是自反的,B中没有<e,e>,排除
A中的<a,c>显然不对,应该是<c,a>
再看C,要么是哈斯图里面有的边,要么是传递性推出的边,因此正确
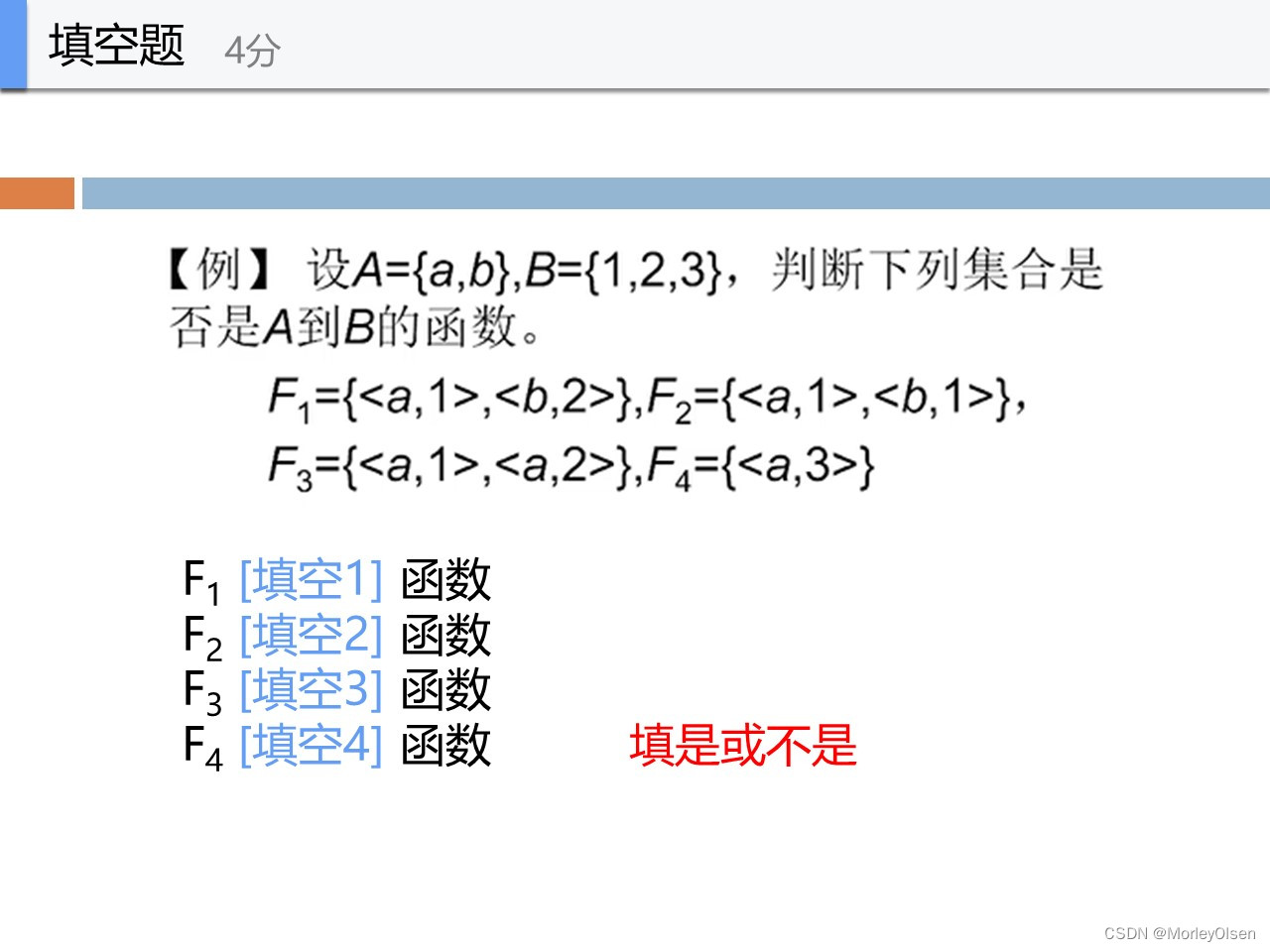
是
是
不是
不是
F1和F2中A所有元素都有映射
F3和F4中没有b的映射,且F3不满足唯一性

C
A中存在一对多的关系,例如x1=1时,x2可以取2、3、4...
B中存在一对多的关系,例如y1=4时,y2可以是2、-2
C是一对一的关系
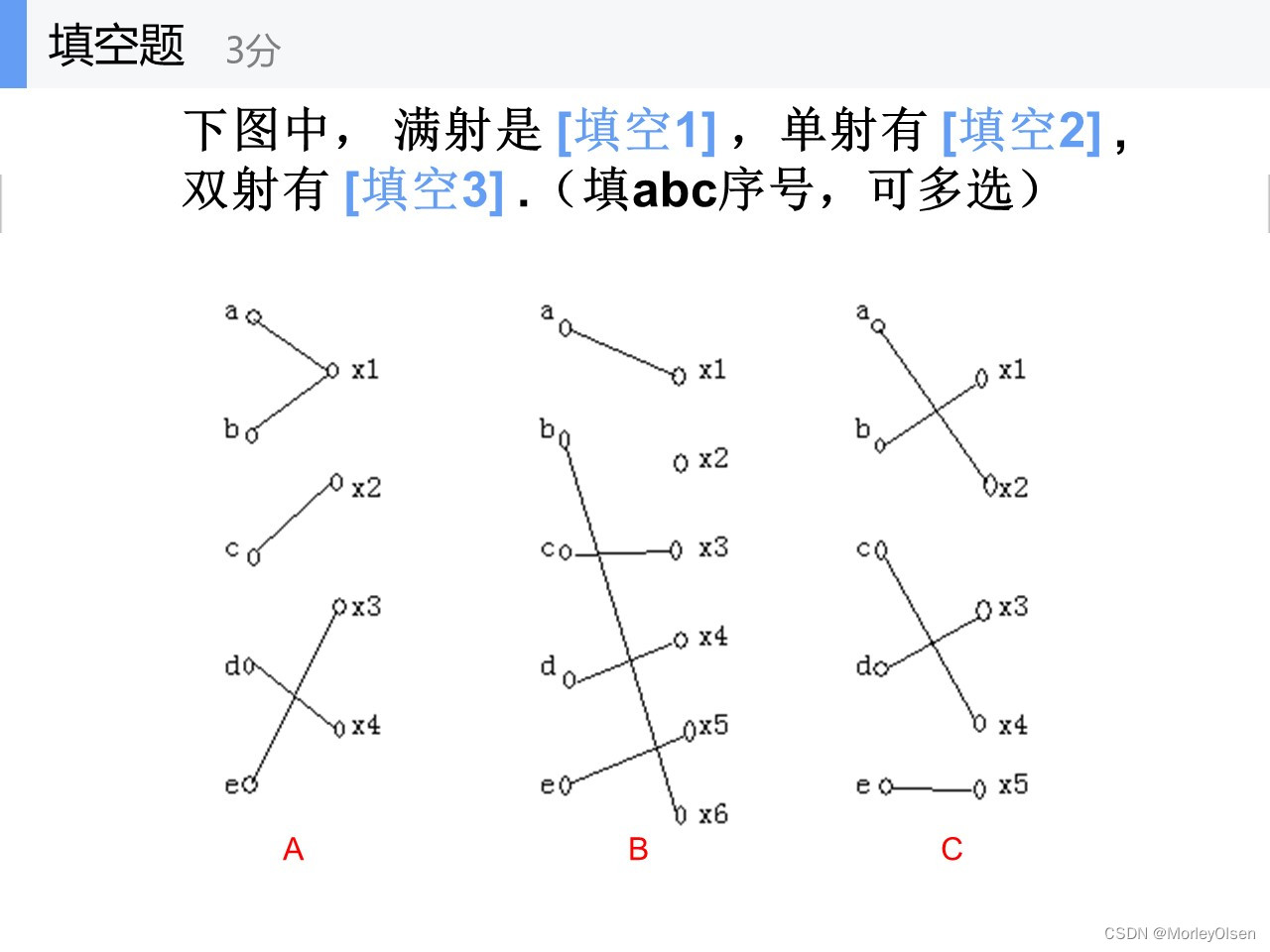
AC
BC
C
满射需要Y中的每个元素都被映射,因此B不满足(x2没有被映射)
单射需要Y中的被映射元素是唯一映射的,因此A不满足(x1被映射2次)
双射需要同时满足上面两点








 文章讨论了数学中的二元关系、笛卡尔积的概念,以及实数与自然数的比较,涉及自反性、传递性和偏序关系等概念在不同问题中的应用。还分析了布尔逻辑和集合论中的元素映射规则,以及函数的满射、单射和双射特性。
文章讨论了数学中的二元关系、笛卡尔积的概念,以及实数与自然数的比较,涉及自反性、传递性和偏序关系等概念在不同问题中的应用。还分析了布尔逻辑和集合论中的元素映射规则,以及函数的满射、单射和双射特性。























 1932
1932

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










