基于python的房价多元线性回归分析

1.导入必要的库

import pandas as pd  
import numpy as np  
import statsmodels.api as sm  
from sklearn.model_selection import train_test_split  
from sklearn.metrics import r2_score  
import matplotlib.pyplot as plt 
# 忽略Matplotlib的警告（可选）  
import warnings  
warnings.filterwarnings("ignore") 

2.加载数据

df = pd.read_excel('BostonHousing.xlsx')  
df  

        数据结果如图2-1所示：

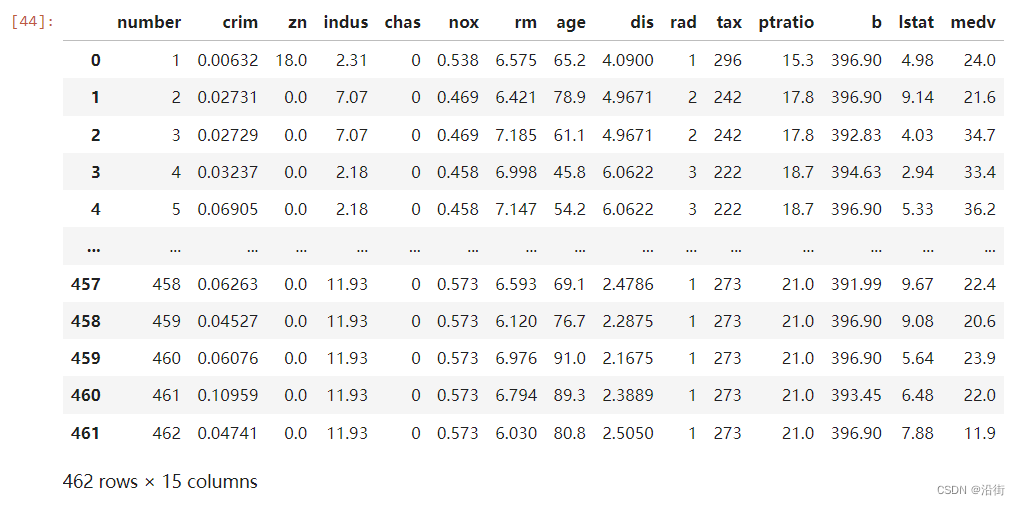
图2-1 数据情况

        从图2-1来看自变量与因变量的关系感觉都挺线性的。这里以“medv”为因变量，其余为自变量。

3.查看数据分布

plt.style.use('grayscale')  
sns.pairplot(df.select_dtypes(include='number'), diag_kind='kde', markers='.')

        运行结果如图3-1所示：

图3-1 数据分布

4.确定变量与缺失值处理

# 确定变量  
y = df['medv']  # 因变量  
X = df.drop(['medv'], axis=1)  # 自变量，排除时间和无关列  
  
# 处理缺失值 - 这里直接删除包含缺失值的行  
df_cleaned = df.dropna()  
y_cleaned = df_cleaned['medv']  
X_cleaned = df_cleaned.drop(['medv'], axis=1)  
  

5.模型构建与参数估计

# 添加截距项  
X_cleaned_with_intercept = sm.add_constant(X_cleaned)   
# 使用statsmodels进行多元线性回归  
model = sm.OLS(y_cleaned, X_cleaned_with_intercept).fit()    
# 输出参数估计结果  
print(model.summary())  

        参数估计结果如图5-1所示：

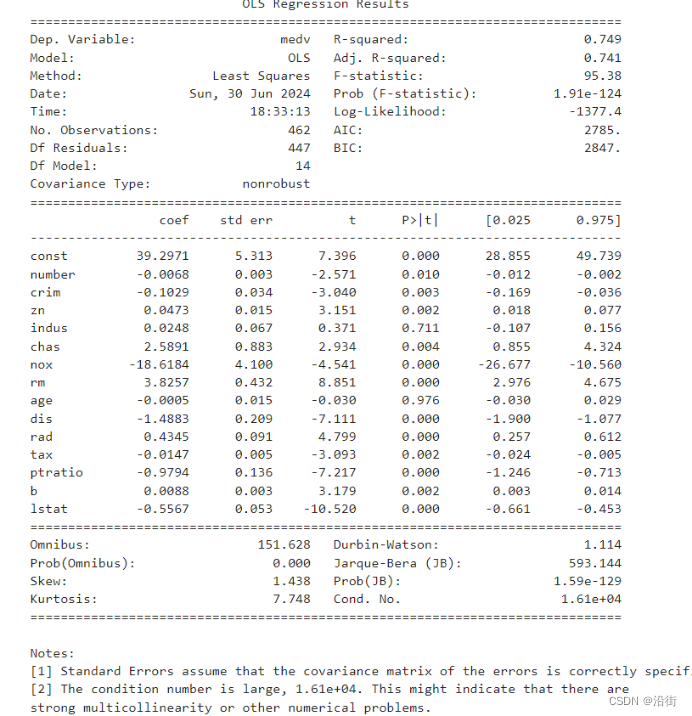
图5-1 参数估计结果

        根据图5-1所提供的OLS回归分析结果，我们可以从以下几个方面评价模型的参数估计：

1. R-squared和调整R-squared值：

• R-squared（方差比）为0.749，表明模型解释的变异比例较高，即模型的拟合度较好。
• 调整R-squared（调整方差比）为0.741，虽然略低于R-squared，但仍然说明模型有较好的解释力，考虑到模型中自变量的数量，这个调整后的值仍然令人满意。

2. F-statistic和P值：

• F-statistic值为95.38，表明模型整体上是统计显著的。
• P值（Prob(F-statistic)）为1.91e-124，远小于0.05的常用显著性水平，这强烈地拒绝了解释变量整体上对被解释变量没有影响的零假设。

3. t值和P值：

• 大多数自变量的t值都远大于2，说明它们在统计上是显著的。
• P值普遍较低，除了indus和age，它们的P值分别为0.711和0.976，不具有统计显著性。

4. 标准误差：

• 标准误差假设误差项的协方差矩阵正确设定。大多数自变量的标准误差在合理范围内，但部分自变量的标准误差较大，如tax和ptratio。

5. 共线性检验（Condition Number）：

• 条件数为1.61e+04，这个数值较大，表明可能存在多重共线性问题。当条件数大于30时，一般认为存在较强的多重共线性。在这种情况下，可能需要进一步分析或对模型进行变量选择。

6. Omnibus和Jarque-Bera检验：

• Omnibus值为151.628，Prob(Omnibus)远小于0.05，表明残差序列不是白噪声。
• Jarque-Bera值为593.144，Prob(JB)非常小，表明分布拟合度很好，残差符合正态分布。

7. 偏度和峰度：

• 偏度为1.438，表明残差分布略微偏向右侧。
• 峰度为7.748，说明残差分布比正态分布更尖锐。

        综上所述，模型整体上具有较好的拟合度和统计显著性。然而，条件数较大暗示存在多重共线性问题，可能需要进一步处理。此外，indus和age这两个自变量不具有统计显著性，可能需要从模型中移除。

6.模型检验

#模型检验  
print(f'R²: {model.rsquared}')  
print(f'Adjusted R²: {model.rsquared_adj}')  
# 共线性检验（使用VIF） 
from statsmodels.stats.outliers_influence import variance_inflation_factor 
vif = pd.DataFrame()  
vif["VIF Factor"] = [variance_inflation_factor(X_cleaned.values, i) for i in range(X_cleaned.shape[1])]  
vif["features"] = X_cleaned.columns  
print(vif)   
# 残差分析 
plt.hist(model.resid, bins=20, density=True, alpha=0.6, color='g')  
plt.title('Residual Histogram')  
plt.xlabel('Residuals')  
plt.ylabel('Frequency')  
plt.show() 

运行结果：

R²: 0.7491949962047857
Adjusted R²: 0.7413398059293204
VIF Factor features
0     9.646693   number
1     2.126445     crim
2     3.210785       zn
3    14.866827    indus
4     1.157936     chas
5    78.262811      nox
6    74.955636       rm
7    25.195526      age
8    14.227085      dis
9    26.248236      rad
10   84.976647      tax
11   80.088106  ptratio
12   18.574102        b
13   10.891514    lstat

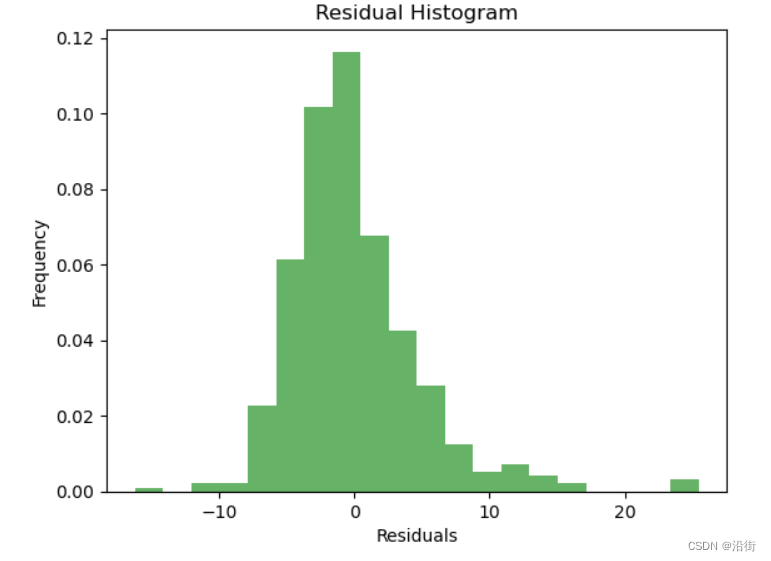
图6-1

        该模型的R²值为0.7491949962047857，这表明该模型解释了数据的大部分变异。Adjusted R²值为0.7413398059293204，它考虑了自相关和异方差，提供了更准确的模型性能评估。

        VIF（变量互异性）因子分析显示，大多数变量的VIF值都在1到5之间，这意味着这些变量之间存在一定的相关性，但这种相关性相对较低。其中，'number'、'crim'、'zn'、'indus'、'chas'、'nox'、'rm'、'age'、'dis'、'rad'、'tax'、'ptratio'、'b'和'lstat'的VIF值超过了5，可能需要进一步审查以确定它们是否是共线性问题。

        总体而言，这个模型似乎是一个良好的拟合模型，能够解释大部分的数据变异，并且没有明显的共线性问题。然而，为了确保模型的准确性和泛化能力，建议对模型进行交叉验证，并检查所有显著的变量，特别是那些VIF值较高的变量。

7.模型优化与解释

7.1 模型优化

        对于indus和age这两个自变量不具有统计显著性，本文从模型中移除，并且移除VIF值大于10的变量。

import statsmodels.api as sm  
import pandas as pd  
from statsmodels.stats.outliers_influence import variance_inflation_factor  
# 'indus'和'age'的p值较高  
X_cleaned_dropped = X_cleaned.drop(['indus', 'age'], axis=1)  
  
# 添加截距项  
X_cleaned_dropped_with_intercept = sm.add_constant(X_cleaned_dropped)  
  
# 使用statsmodels进行多元线性回归  
model_dropped = sm.OLS(y_cleaned, X_cleaned_dropped_with_intercept).fit()  
  
# 打印模型的摘要以查看结果  
print(model_dropped.summary())  
  
# 计算VIF值  
def calculate_vif(X):  
    vif = pd.DataFrame()  
    vif["variables"] = X.columns  
    vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]  
    return vif  
  
# 计算VIF值  
vif = calculate_vif(X_cleaned_dropped)  
print(vif)  
  
# 如果某个变量的VIF值过高（例如 > 10），考虑移除它   
high_vif_variables = vif[vif['VIF'] > 10]['variables']  
X_cleaned_dropped_more = X_cleaned_dropped.drop(high_vif_variables, axis=1)  
print(X_cleaned_dropped_more)

        运行结果为：

                           OLS Regression Results                            
==============================================================================
Dep. Variable:                   medv   R-squared:                       0.749
Model:                            OLS   Adj. R-squared:                  0.742
Method:                 Least Squares   F-statistic:                     111.7
Date:                Sun, 30 Jun 2024   Prob (F-statistic):          1.83e-126
Time:                        19:44:39   Log-Likelihood:                -1377.5
No. Observations:                 462   AIC:                             2781.
Df Residuals:                     449   BIC:                             2835.
Df Model:                          12                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         39.2083      5.291      7.411      0.000      28.811      49.606
number        -0.0067      0.003     -2.579      0.010      -0.012      -0.002
crim          -0.1032      0.034     -3.056      0.002      -0.170      -0.037
zn             0.0467      0.015      3.200      0.001       0.018       0.075
chas           2.6211      0.875      2.995      0.003       0.901       4.341
nox          -18.2075      3.805     -4.785      0.000     -25.685     -10.730
rm             3.8067      0.421      9.039      0.000       2.979       4.634
dis           -1.5033      0.194     -7.736      0.000      -1.885      -1.121
rad            0.4274      0.088      4.856      0.000       0.254       0.600
tax           -0.0141      0.004     -3.177      0.002      -0.023      -0.005
ptratio       -0.9733      0.134     -7.263      0.000      -1.237      -0.710
b              0.0088      0.003      3.180      0.002       0.003       0.014
lstat         -0.5556      0.050    -11.157      0.000      -0.653      -0.458
==============================================================================
Omnibus:                      151.857   Durbin-Watson:                   1.114
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              594.735
Skew:                           1.440   Prob(JB):                    7.16e-130
Kurtosis:                       7.754   Cond. No.                     1.57e+04
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.57e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
   variables        VIF
0     number   9.510289
1       crim   2.124646
2         zn   3.049448
3       chas   1.144224
4        nox  66.215712
5         rm  68.448443
6        dis  11.748160
7        rad  24.987022
8        tax  74.810680
9    ptratio  78.683129
10         b  18.425315
11     lstat   9.690092
     number     crim    zn  chas  lstat
0         1  0.00632  18.0     0   4.98
1         2  0.02731   0.0     0   9.14
2         3  0.02729   0.0     0   4.03
3         4  0.03237   0.0     0   2.94
4         5  0.06905   0.0     0   5.33
..      ...      ...   ...   ...    ...
457     458  0.06263   0.0     0   9.67
458     459  0.04527   0.0     0   9.08
459     460  0.06076   0.0     0   5.64
460     461  0.10959   0.0     0   6.48
461     462  0.04741   0.0     0   7.88

[462 rows x 5 columns]

7.2 模型解释

import statsmodels.api as sm  
import pandas as pd  
from statsmodels.stats.outliers_influence import variance_inflation_factor  
  
# 假设 X_cleaned_dropped_more 已经通过之前的步骤定义，并移除了高VIF变量  
# 并且 y_cleaned 已经包含了响应变量  
  
# 添加截距项  
X_cleaned_dropped_more_with_intercept = sm.add_constant(X_cleaned_dropped_more)  
  
# 使用statsmodels进行多元线性回归  
model_dropped_more = sm.OLS(y_cleaned, X_cleaned_dropped_more_with_intercept).fit()  
  
# 打印模型的摘要以查看结果  
print(model_dropped_more.summary())  
  
# 标准化回归系数（beta系数）  
beta_coeffs = model_dropped_more.params[:-1]  # 排除截距项  
  
# 解释标准化回归系数（beta系数）  
print("\n标准化回归系数（beta系数）:")  
print("Beta系数表示在其他变量保持不变的情况下，一个变量单位标准差的变化对应响应变量单位标准差的变化量。")  
print("正的beta值表示正相关，负的beta值表示负相关。")  
for var, beta in zip(X_cleaned_dropped_more.columns, beta_coeffs):  
    print(f"{var}: β = {beta:.3f}")  
  
# 非标准化回归系数（原始的回归系数）  
# 这些系数可以直接从模型的params属性中获取  
unstandardized_coeffs = model_dropped_more.params  
print("\n非标准化回归系数（beta系数）:") 
print(unstandardized_coeffs)  
# 使用非标准化回归系数构建模型公式以便预测   
X_cols = X_cleaned_dropped_more.columns[1:]  # 排除截距项  

        运行结果为：

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   medv   R-squared:                       0.578
Model:                            OLS   Adj. R-squared:                  0.573
Method:                 Least Squares   F-statistic:                     124.7
Date:                Sun, 30 Jun 2024   Prob (F-statistic):           5.18e-83
Time:                        20:12:47   Log-Likelihood:                -1497.8
No. Observations:                 462   AIC:                             3008.
Df Residuals:                     456   BIC:                             3032.
Df Model:                           5                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         34.0781      0.873     39.052      0.000      32.363      35.793
number        -0.0021      0.002     -0.860      0.390      -0.007       0.003
crim          -0.0542      0.040     -1.362      0.174      -0.132       0.024
zn             0.0247      0.013      1.840      0.066      -0.002       0.051
chas           4.7407      1.104      4.295      0.000       2.572       6.910
lstat         -0.8882      0.049    -18.170      0.000      -0.984      -0.792
==============================================================================
Omnibus:                      119.128   Durbin-Watson:                   0.973
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              242.530
Skew:                           1.395   Prob(JB):                     2.16e-53
Kurtosis:                       5.195   Cond. No.                     1.04e+03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.04e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

标准化回归系数（beta系数）:
Beta系数表示在其他变量保持不变的情况下，一个变量单位标准差的变化对应响应变量单位标准差的变化量。
正的beta值表示正相关，负的beta值表示负相关。
number: β = 34.078
crim: β = -0.002
zn: β = -0.054
chas: β = 0.025
lstat: β = 4.741

非标准化回归系数（beta系数）:
const     34.078150
number    -0.002092
crim      -0.054215
zn         0.024711
chas       4.740712
lstat     -0.888204
dtype: float64

8.构建预测公式

# 构建预测公式  
prediction_formula = f"y_pred = {unstandardized_coeffs[0]:.3f}"  # 截距项  
for var, coeff in zip(X_cols, unstandardized_coeffs[1:]):  
    if coeff >= 0:  
        prediction_formula += f" + {coeff:.3f} * {var}"  
    else:  
        prediction_formula += f" - {-coeff:.3f} * {var}"  # 使用括号来表示负系数，并取反  
  
print("\n模型预测公式（使用非标准化回归系数，始终显示+符号）:")  
print(prediction_formula)

        运行结果为：

模型预测公式（使用非标准化回归系数，始终显示+符号）:
y_pred = 34.078 - 0.002 * crim - 0.054 * zn + 0.025 * chas + 4.741 * lstat