数据结构第五章树的笔记

树的定义：

树是n个结点的集合

当n=0时为空树

树的一些术语

1度：结点下面子节点的数量，树的度为最大子结点数量

2层次：即根结点到该结点的层数

3树的深度：树的最大层次

4叶结点（终端结点）：即没有子结点的结点

5分支结点：有子结点的结点

树是一种递归的数据结构（即自己调用自己）

以上是我对数据结构树的定义的理解

二叉树

二叉树的性质：

性质1: 在二叉树的第 i 层上至多有 2 i − 1 个结点 ，第i层上至少有 1个结点？
性质2: 深度为k的二叉树至多有2k-1个结点，深度为k时至少有 k 个结点？
性质3: 对于任何一棵二叉树，若2度的结点数有n2个，则叶子数n0必定为n2＋1 （即n0=n2+1）

性质4：具有n个结点的完全二叉树的深度必为[log2n]+1

性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2。

特殊形态的二叉树：

满二叉树：即除了最下面一排其他结点都有两个子节点的二叉树

完全二叉树：与完全二叉树是包含关系，右边最下面一层允许缺少若干连续结点

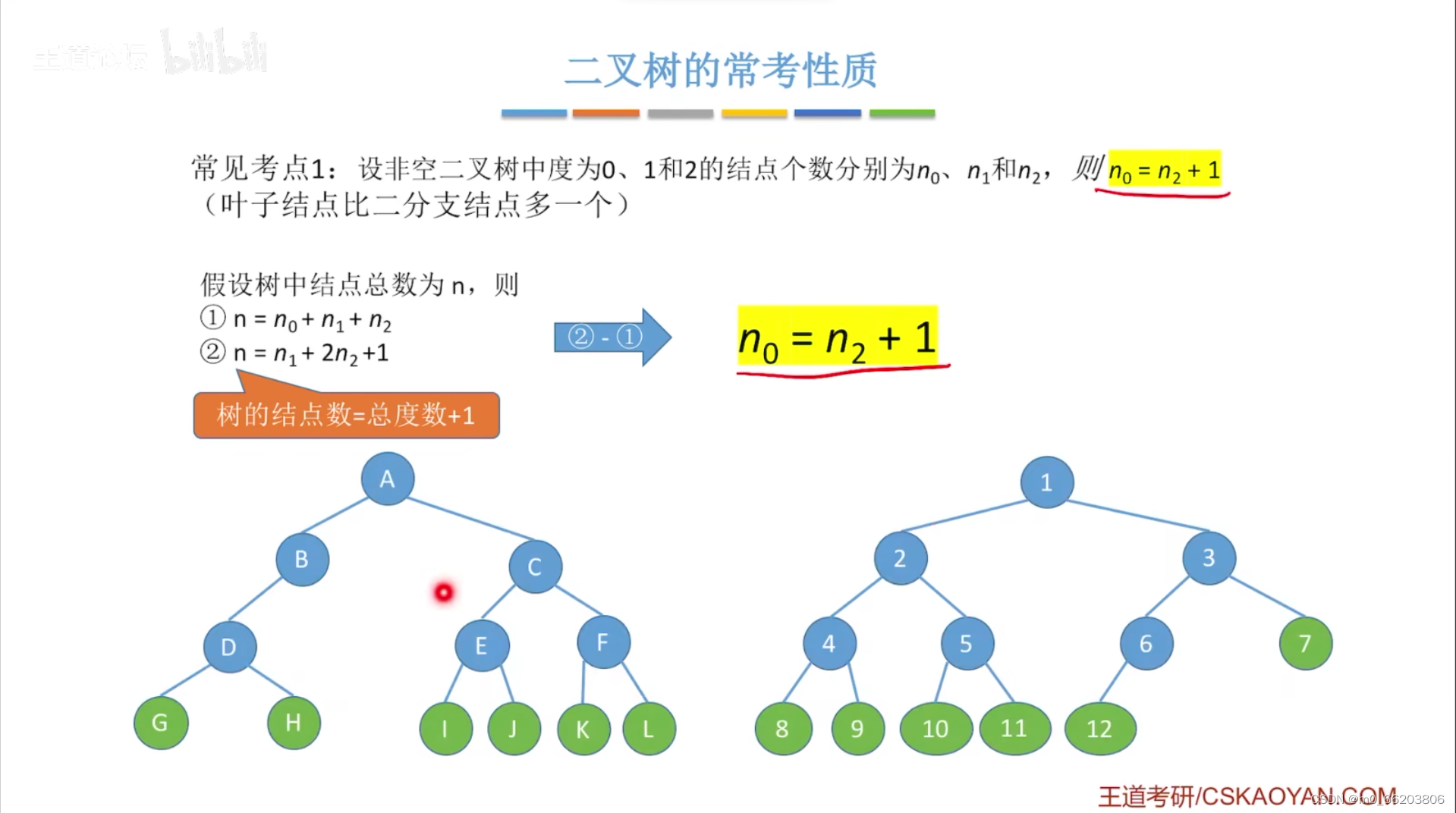
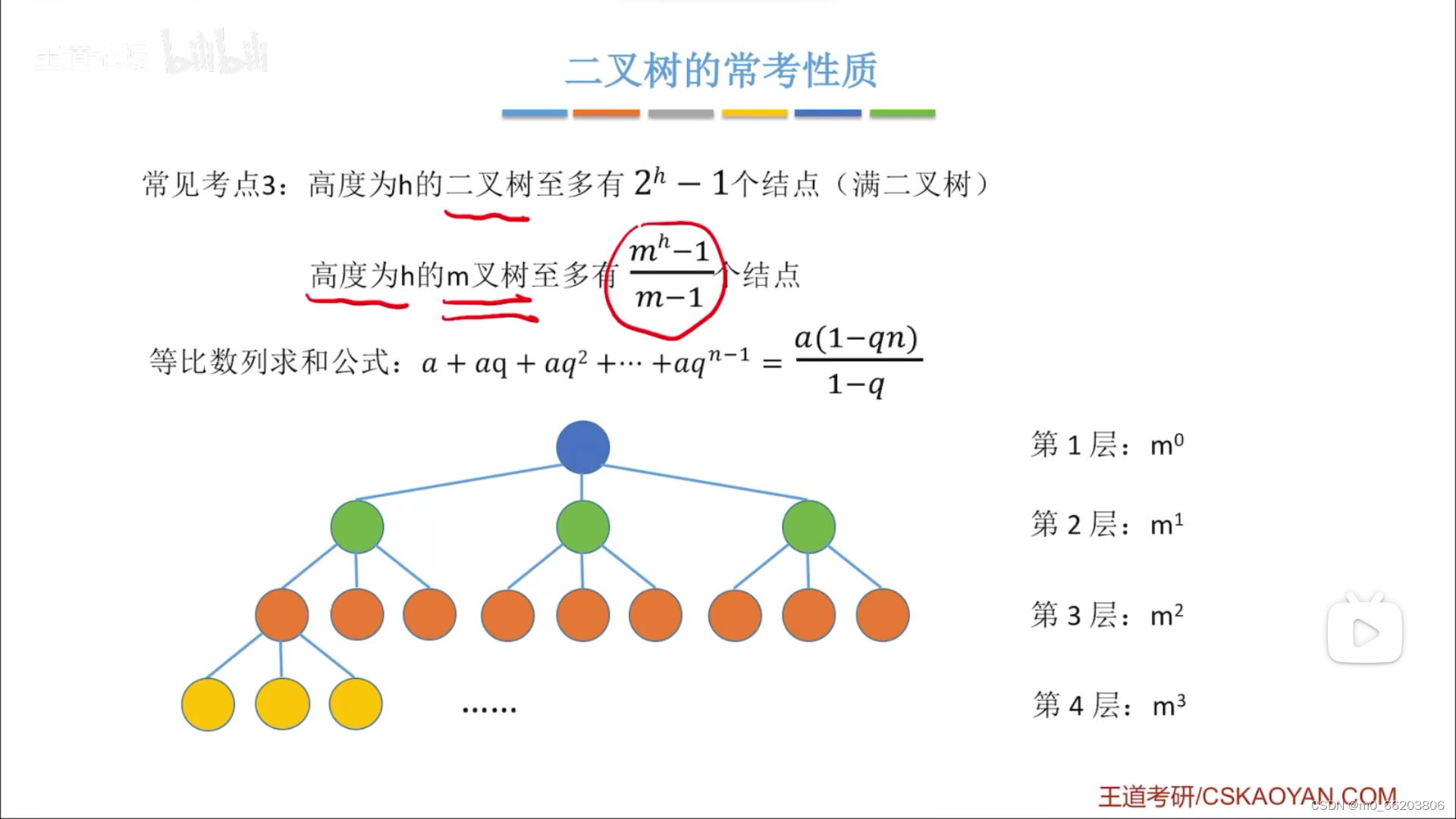
二叉树的一些常考性质：

1m叉树第i层至多有m^i-1个结点

2高度为h的m叉树至多有吗m^h-1/m-1个结点

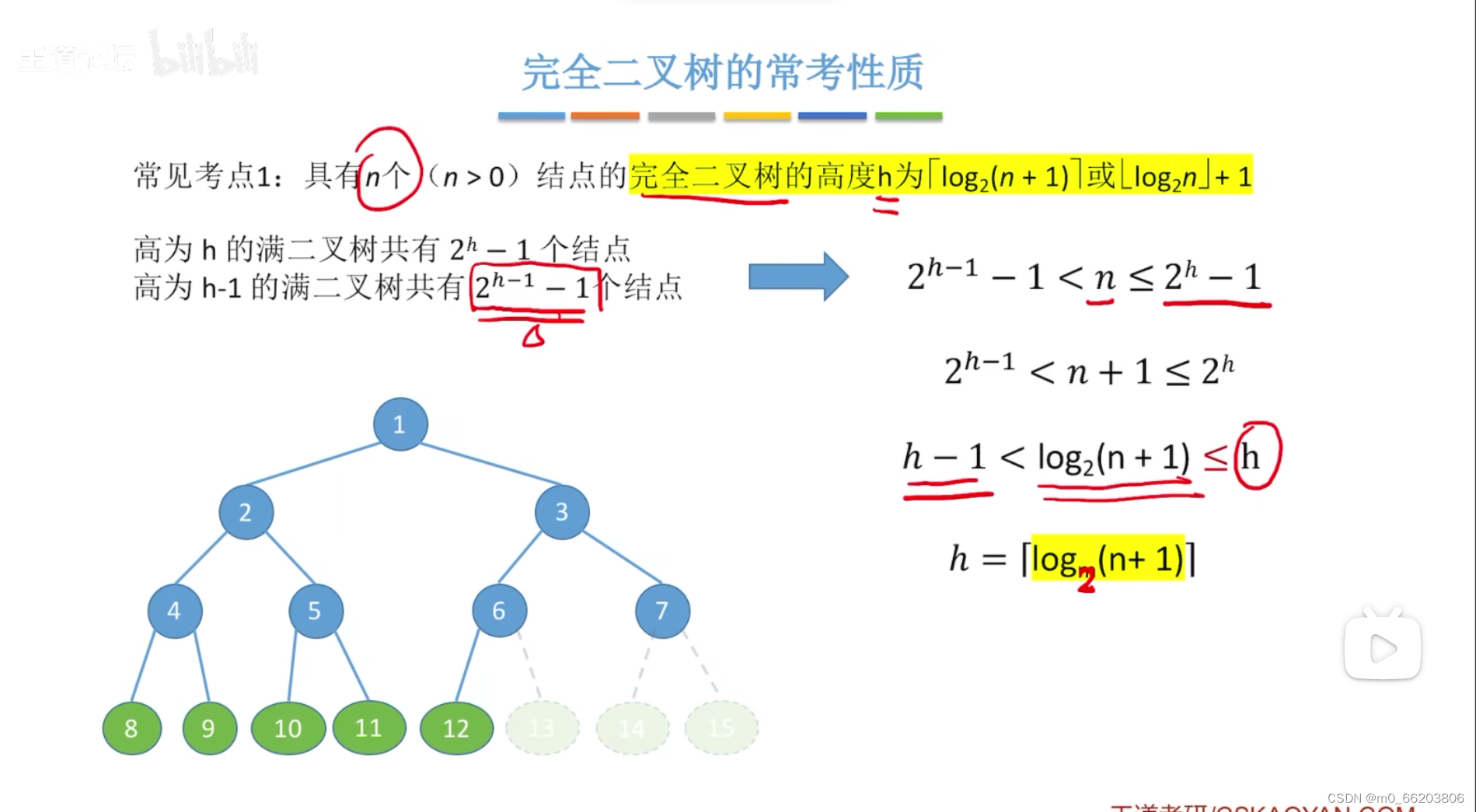
完全二叉树的一些常考性质：

1.完全二叉树的上限和下限：2^h-1<n<=2^h -1

2有n个结点的二叉树的高度h为log2(n+1)

1. 定义和属性

• 二叉树：每个节点最多有两个子节点的树结构。
• 节点：二叉树的每个元素称为节点。
• 根：二叉树的顶部节点称为根。
• 左子树：节点的左子节点及其后代构成的子树。
• 右子树：节点的右子节点及其后代构成的子树。
• 叶子节点：没有子节点的节点。
• 深度和高度：二叉树的深度是最长路径上边的数量，高度是根到叶子的边数。

2. 遍历

• 前序遍历：先访问根节点，然后左子树，最后右子树。
• 中序遍历：先左子树，然后根节点，最后右子树。
• 后序遍历：先左子树，然后右子树，最后根节点。
• 层序遍历：按照从上到下，从左到右的顺序访问。

3. 性质

• 二叉搜索树：左子树上的节点值小于根节点，右子树上的节点值大于根节点。
• 平衡二叉树：任何两个叶子节点的深度之差不超过1。
• 完全二叉树：除了最后一层外，每一层都被完全填满，且最后一层的节点尽可能地靠左排列。

4. 操作和算法

• 插入：在二叉搜索树中插入新节点。
• 删除：从二叉搜索树中删除节点。
• 搜索：在二叉搜索树中查找特定值。
• 查找最小值/最大值：在二叉树中找到最小或最大值的节点。
• 计算树的高度：确定二叉树的高度。

5. 复杂度分析

• 时间复杂度：大多数二叉树的操作时间复杂度为O(n)，其中n是树中节点的数量。但在最佳情况下，如二叉搜索树的查找、插入和删除操作，时间复杂度为O(log n)。
• 空间复杂度：遍历算法的空间复杂度通常为O(h)，其中h是树的高度。

6. 应用场景

• 数据库索引：使用B树或B+树作为索引结构。
• 文件系统：使用二叉树来管理文件元数据。
• 表达式解析：使用二叉树来表示和解析数学表达式。

7. 特殊类型的二叉树

• 二叉搜索树：一种特殊的二叉树，其中每个节点的左子树上的值小于该节点，右子树上的值大于或等于该节点。
• AVL树：一种自平衡二叉搜索树，其中任何两个叶子节点的深度之差不超过1。
• 红黑树：一种自平衡二叉搜索树，通过颜色编码确保最长路径不超过最短路径的两倍。

8. 编码实现

实现二叉树通常涉及创建一个节点类（或结构体），以及相应的树类来管理这些节点。

// 定义二叉树节点
typedef struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

// 创建一个新的二叉树节点
TreeNode* createNode(int val) {
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->val = val;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 示例：中序遍历二叉树
void inorderTraversal(TreeNode* root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->val);
        inorderTraversal(root->right);
    }
}

}

哈夫曼树的知识点，哈夫曼是什么？，为什么需要存在？，怎么用代码表示哈夫曼树？

1. 哈夫曼树概述

哈夫曼树是一种特殊的二叉树，用于数据压缩领域的霍夫曼编码（Huffman Coding）。它由David A. Huffman在1952年发明，目的是在不产生任何冲突的情况下，为不同字符生成一个唯一的变长码。

2. 哈夫曼树的性质

• 一棵哈夫曼树是一棵完整的二叉树。
• 每个叶子节点代表一个字符，非叶子节点代表子树中所有字符的频率。
• 所有叶子节点都在同一层级。
• 树中没有两颗节点具有相同的频率。

3. 哈夫曼编码

• 哈夫曼编码是一种贪心算法，它根据字符出现频率生成编码。
• 字符频率越高，其哈夫曼编码越短。
• 编码是唯一的，并且是前缀码，即没有一个字码是另一个字码的前缀。

4. 构建哈夫曼树的步骤

1. 统计所有字符出现的频率。
2. 创建一个优先队列（最小堆），将所有字符作为节点加入。
3. 当优先队列中还有超过一个节点时：
   • 从优先队列中移除两个最小频率的节点。
   • 创建一个新的内部节点，其频率是两个节点频率之和。
   • 将这两个节点作为新节点的子节点。
   • 将新节点加入优先队列。
4. 重复步骤3，直到优先队列中只剩下一个节点，这个节点就是哈夫曼树的根。

5. 学习中遇到的问题和思考

• 频率相同的字符：当遇到频率相同的字符时，哈夫曼树的构建过程可能会产生多棵树，因为选择的顺序会影响最终的树结构。
• 树的平衡性：哈夫曼树不一定是平衡的，这可能影响编码的效率。在某些情况下，可能会考虑使用其他类型的树，如平衡二叉树，以提高效率。
• 变长编码的优缺点：变长编码可以有效地压缩数据，但同时也可能使得数据流的解析变得更加复杂，需要额外的边界标记。
• 实际应用中的考虑：在实际的数据压缩应用中，除了考虑压缩率，还需要考虑编码和解码的时间复杂度以及实现的复杂性。