【机器学习西瓜书第二章模型评估与选择学习笔记和习题探讨】

本文链接：https://blog.csdn.net/m0_67405031/article/details/131855562

第2章模型评估与选择

写在前面的话：
作为新手，第一次使用CSDN博客markdown。B站8分钟学会！使用markdown编辑以及 Latex （Katex）数学公式在markdow 的短视频让我顺利上手，其网址为： https://www.bilibili.com/video/av92772280/vd_source=cc5c179fd988f2c41e58b9c7744c8b17。
感谢作者分享。

一、几个定义

 设定m个样本：
 有a个样本分类错误，真正例为TP，假真例为FP，假反例为FN，正反例为TN。

错误率E	精度ACC	查准率P	查全率R	平衡点B	F1度量	真正比例TPR	假正例率
$a / m$	$1 - E$	$\frac{TP}{TP+FP}$	$\frac{TP}{TP+FN}$	$P = R$	$\frac{2\times P\times R}{P+R}$	$\frac{TP}{TP+FN}$	$\frac{FP}{TP+FP}$

二、训练集和测试集获取方法

1 留出法

    策略：将数据集D划分为两个互斥集合S和T。其中，S为训练集，T为测试集。
    优点：划分简单。
    不足：若S过大，训练结果可能更接近D训练出的模型，但T较小，则评估结果
    可能不够稳定准确。反之，训练结果和D相比可能有较大差别，从而降低评估
    结果保真性。中观做法是S和T比例范围大致为2/3~4/5。

2 k交叉验证法

  策略：将数据集D划分为K个大小相似的互斥子集。每个子集都尽可能保持数据
  分布一致性。每次将某个子集作为测试集，而剩余K-1个子集作为训练集。第二
  次选择另外一个子集作为测试集，如此轮流	。该方法评估结果稳定性和保真性
  取决于K的取值。
  演变形式：对K的取值方法随机进行P次重复划分，最终评估结果是这P次K折交
  叉验证结果的平均。
  极端形式：将数据集中每一个样本作为一次测试集，而其他剩余全是训练集。这
  种方法称为留一法。测试结果通常比较准确，但计算开销巨大。

3 自助法

 设定数据集D含有m个样本。设定一个空集D',每次随机从D中抽出一个样本放入
 D'中，直到D'中装满m个样本为止。D'作为训练集，D\D'作为测试集。
 该方法课用于数据集较小，难以有效划分训练测试集场景。由于自助法产生数据
 集改变了初始数据集的分布，会引入估计偏差，所以在数据量充足时，留出法和
 交叉验证法更常用一些。

三性能度量

1、性能度量定义：
为了对学习器泛化性能进行评估，需要衡量模型泛化能力的评价标准。这就是性
能度量。
回归任务中，最常用的性能度量是“均方误差”。

$E(f:D)=\frac{1}{m}\textstyle\sum_{i=1}^m(f(x_i)-y_i)^2$

2、性能衡量策略

  （1）  P-R曲线与平衡点
    P，R定义参加第一部分表格说明。

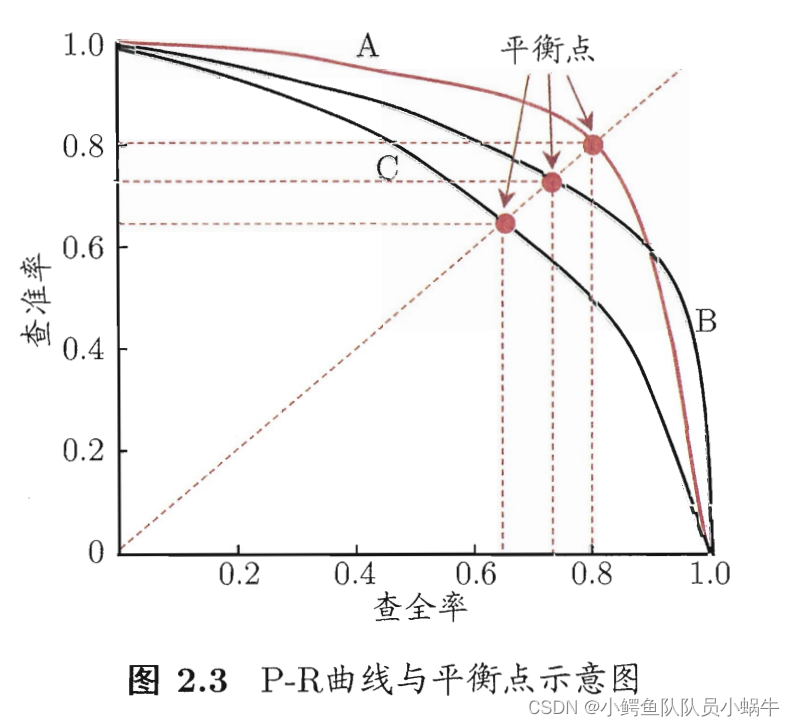
在这里插入图片描述

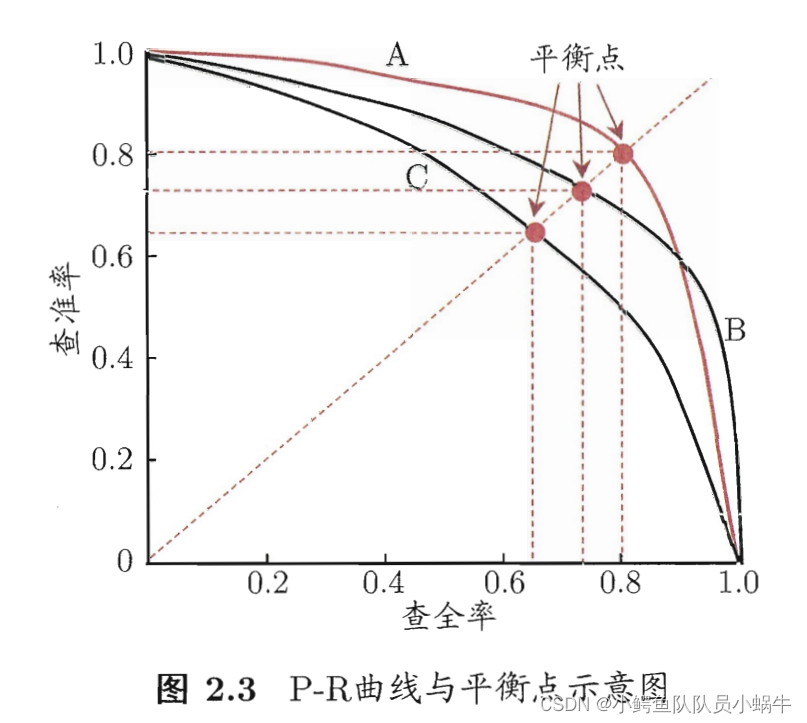
![![此图拷贝周志华《机器学习》P31](https://img-
blog.csdnimg.cn/77a0e376471c4f239f25b9ebd403fbaf.png)

鉴于查准率P和查全率R的一对矛盾性，通常通过P-R曲线，找出平衡点BEP（此处：P=R），
以及曲线包围面积，作为衡量学习器性能优劣的评判准则。
   进一步拓展，还有在BEP基础上，给出了F1度量，$F_\beta$度量和微F1度量方法。有兴趣读
   者可参加周志华老师《机器学习》西瓜书P32页。      
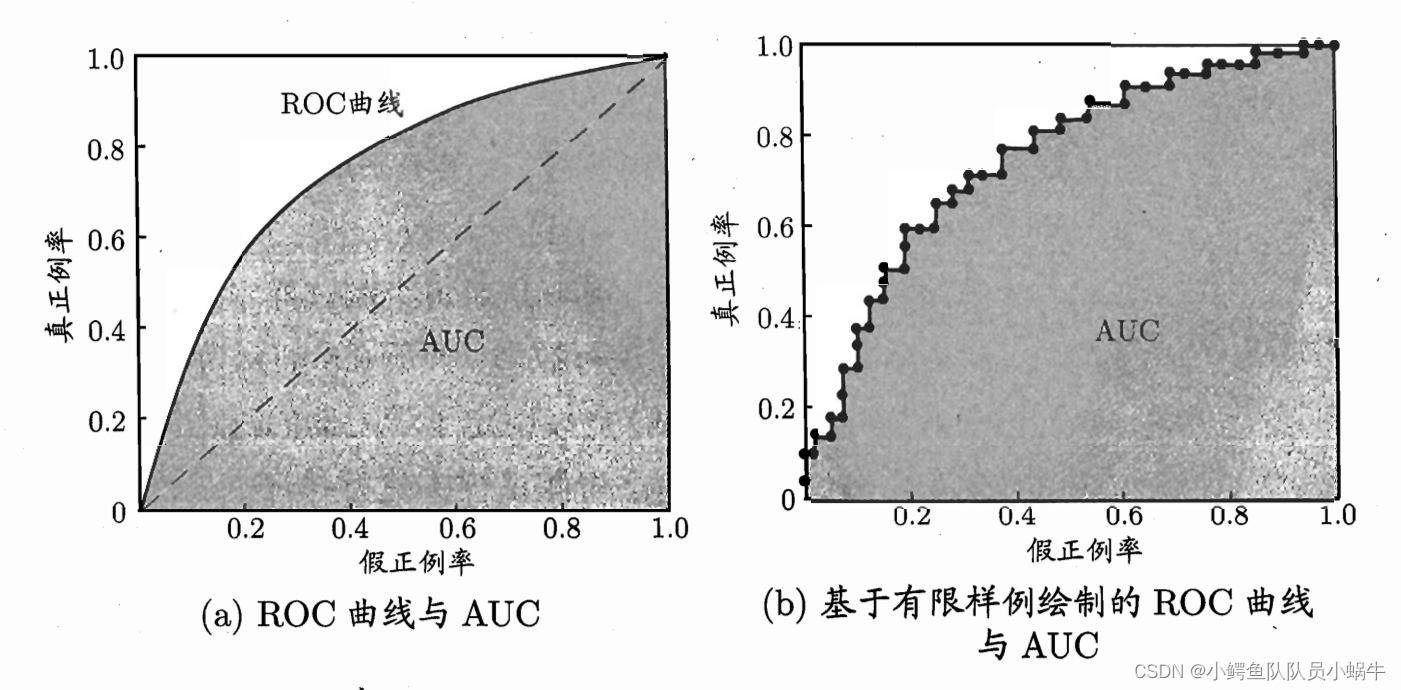
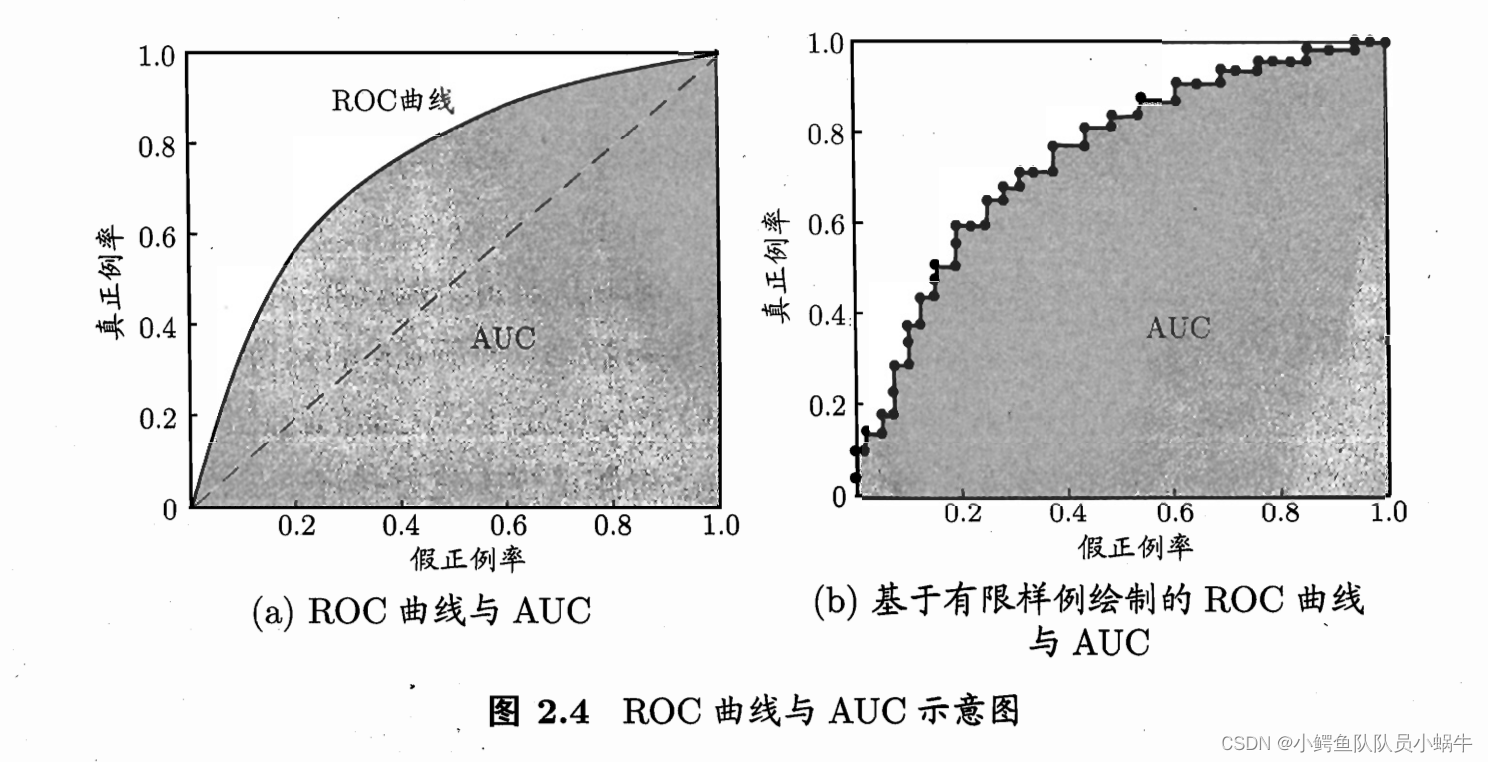
   （2）ROC与AUC
   ROC是指真正例率TPR和假正例率FPR之间曲线。
   AUC指ROC和坐标轴包围的面积。
   通常，被住的ROC的学习器性能更好，AUC面积越大，性能越好。

在这里插入图片描述

   ![此图拷贝周志华《机器学习》P31](https://img-blog.csdnimg.cn/7a6ac07deb9f4196872279b9fc5e8371.png)
（3）代价敏感错误率与代价曲线

3、检验方法
通过实验评估方法测得学习器某个性能度量，由于算法本身随机性以及测试集选择的差异性，为了更好进行性能检验，统计假设检验为学习器性能提供了重要依据。包括假设检验，交叉验证t检验，McNeMar检验。感兴趣的同学，具体统计原理参加《机器学习》原书。

4 偏差与方差
“偏差-方差分解”是解释学习算法泛化性能重要工具。通常偏差与方差的冲突性称为偏差-方差窘境(bias-variance dilemma)如图 2.9所示：
在这里插入图片描述

  偏差度量了学习算法期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力; 方差度
  量了同 样大小的训练集的变动所导致的学习性能的变化, 刻画了数据扰动所造成的 影响。
  在训练不足时, 学习器的拟合能力不够强, 训练数据的扰动不足以使学习器产生显著变化, 此时
  偏差主导了泛化错误率; 
  随着训练程度的加深, 学习器的拟合能力逐渐增强, 训练数据发生的扰动渐渐能被学习器学到, 
  方差逐渐主导了泛化错误率;
   在训练程度充足后, 学习器的拟合能力已非常强, 训练数据发生的轻微扰动都会导致学习器发生
   显著变化, 若训练数据自身的、非全 局的特性被学习器学到了, 则将发生过拟合。

四习题探讨

2.1 数据集包含 1000 个样本, 其中 500 个正例、 500 个反例, 将其划分为包含 $\%$ 样本的训练集和 $\%$ 样本的测试集用于留出法评估, 试估算共有多少种划分方式.
解：（1）按照分布均匀原则，正例和反例中取 $\%$ 样本，则有500个样本取出350个正例和另外500个样本取出350个反例。取出的方案共有：
$c\binom{350}{500}*c\binom{350}{500}$ 种。
（2）若不按照均匀分布，则从1000中取出700个作为训练集，取出方案有：
$c\binom{700}{1000}$ 种。
2.2 数据集包含 100 个样本, 其中正、反例各一半, 假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测), 试给出用 10 折交叉验证法和留一法分别对错误率进行评估所得的结果。
解：按照10折交叉验证法，则可按照随机估计，获得的训练样本属于正、反例各一半，测试集亦然。所以，按照训练样本较多的类别进行确定，则错误和正确机会均等，而按照随机猜测，则错误率为50%。
按照留一法，则每取出一个样本作为测试集，而训练集里的和测试样本相同的比例为49/99<0.5, 所以，误判率为100%。
2.3 若学习器 $\mathrm{A}$ 的 $F 1$ 值比学习器 $\mathrm{B}$ 高, 试析 A 的 BEP 值是否也比 B 高。
解：若 $F A > FB$
则有： $\frac{2TPA}{2TPA+FNA+FPA}>\frac{2TPB}{2TPB+NPB+FPB}$ （1）
对于BER，根据P=R，故可得：
FP=FN（2）
将（2）式代入1式，可得
$\frac{TPA}{TPA+FNA}>\frac{TPB}{TPB+FNB}$
即： $R A = P A > R A = PB$
故试析 A 的 BEP 值也比 B 高。