Python-动态规划（力扣 64.最小路径和）

1.动态规划法的求解过程:

（1）规划子问题：将原问题的求解过程划分为若干个阶段，每个阶段对应一个子问题，并且子问题之间具有重叠关系。

（2）动态规划函数：根据子问题之间的重叠关系找到子问题满足的递推关系式，这个是动态规划法的关键。

（3）填写表格：根据动态规划函数设计表格，以自底向上的方式计算各个子问题的最优值并填表，实现动态规划过程。

     需要强调的是，上述的动态规划过程可以求得子问题的最优值，如果要得到使目标函数取得极值的最优解，通常在动态过程中记录每个阶段的决策，再根据最优决策序列通过回溯构造最优解。

2.优点：

（1）最优保证性：可以保证找到全局最优解，即使对于非线性规划，也能够在每个子阶段寻找最优解，最终找到全局最优解。

（2）效率高：通常可以有效地解决大规模问题，因为它只需要计算和存储已经计算过的子问题，避免了重复计算。

（3）多阶段决策问题的适用性：适用于许多阶段决策问题，如背包问题、最长公共子序列问题等等。

（4）适用范围广泛：可以应用于连续型多阶段决策过程，对于不能用解析形式表达的函数，也可以给出递推关系求值解。

3.缺点：

（1）缺乏严格的逻辑基础：尽管动态规划法在实际应用中取得了良好的效果，但其缺乏严格的数学逻辑基础。

（2）计算复杂度较高：在计算的过程中，可能需要处理大量的中间结果，对于规模大的问题，计算复杂度较高。

（3）难以设计和理解：可能需要一定的数学基础和问题建模能力。

（4）不适用非确定性问题：因为假设输入是确定的。

4.接下来根据动态规划算法的设计思想来解决力扣的 64.最小路径和。

问题描述：给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

​

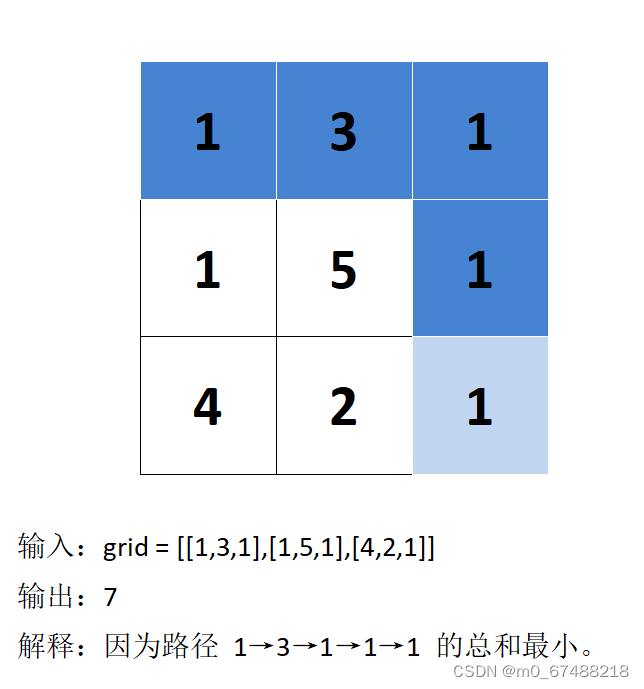
       首先求解初始子问题，由于路径的方向只能是向下或向右的，因此第一行的每个网格都只能从左上角网格开始向右移动到达，第一列的每个网格只能从左上角网格开始向下移动到达，第一行和第一列的每个网格的路径都是唯一的，公式如下：

      考虑重叠子问题，网格(i,j)可以从其上方相邻网格向下移动一步到达，或者从其左方相邻网格向右移动一步到达，最短路径长度等于其上方相邻网格与其左方相邻网格的最短径长度的较小值加上当前网格内的值，公式如下：

综合以上公式对问题进行求解：

初始子问题：

• 填写第一行：dp(1, 1) =  1，dp(1, 2) =  dp(1, 1) + 3 = 4，dp(1, 3) = dp(1,2) + 1= 5。
• 填写第一列：dp(2, 1)= dp(1, 1) + 1 = 2 ，dp(3, 1) =  dp(2, 1)+ 4 = 6。

第一阶段的子问题：

• 填写第二行：dp(2, 2) = min{dp(1, 2), dp(2, 1)} + 5 = 7。

                             dp(2, 3) = min{dp(1, 3), dp(2, 2)} + 1 = 6。

第二阶段的子问题：

1. 填写第三行：dp(3, 2) = min{dp(2, 2), dp(3, 1)} + 2 = 8。

                               dp(3, 3) = min{dp(2, 3), dp(3, 2)} + 1 = 7。

最后，dp(3, 3)即为最小路径和。

解析代码：

定义两个变量m，n作为分别grid的行数和列数。

•    m = len(grid)
•    n = len(grid[0])

创建一个二维列表dp，用于存储动态规划的结果，并初始化dp第一行和第一列。

•    dp = [[0] * n for _ in range(m)]

dp[0][0]表示从起点到终点的最短路径长度。

•    dp[0][0] = grid[0][0] 

第一个循环中，遍历计算每一行 i （从第 1 行到第 m-1 行）的最长上升子序列的长度。   

•    for i in range(1, m):

               dp[i][0] = dp[i-1][0] + grid[i][0]

第二哥循环中，遍历计算每一列 j （从第 1 列到第 n-1 列），的最长上升子序列的长度。

•    for j in range(1, n):

               dp[0][j] = dp[0][j-1] + grid[0][j]

然后使用一个嵌套循填写每一行，dp[i-1][j]和dp[i][j-1]分别表示从起点到grid[i][j]位置的长度，然后将这两个值相加并更新dp[i][j]的值。这里使用了min()函数来选择从上方或左侧到达当前位置的路径长度中的较小值，这样可以确保最终的到的路径是最短的

•    for i in range(1, m):

               for j in range(1, n):

                    dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]

最后，代码返回dp[m-1][n-1]的值，即起点到终点的最短路径长度。

•    return  dp[m-1][n-1]

该算法的时间复杂度为   

完整代码如下：

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        dp = [[0] * n for _ in range(m)]
        dp[0][0] = grid[0][0]
        for i in range(1, m):
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for j in range(1, n):
            dp[0][j] = dp[0][j-1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
        return  dp[m-1][n-1]