数据结构与算法--2.线性表_链表（循环链表、双向链表与双循环链表）

  书接上文：

  上次学到了单链表的一些事情。

  针对单链表的一些问题，我们推出了它的加强版。

 1.循环链表

循环链表：又是我的丑丑笔记，哈哈

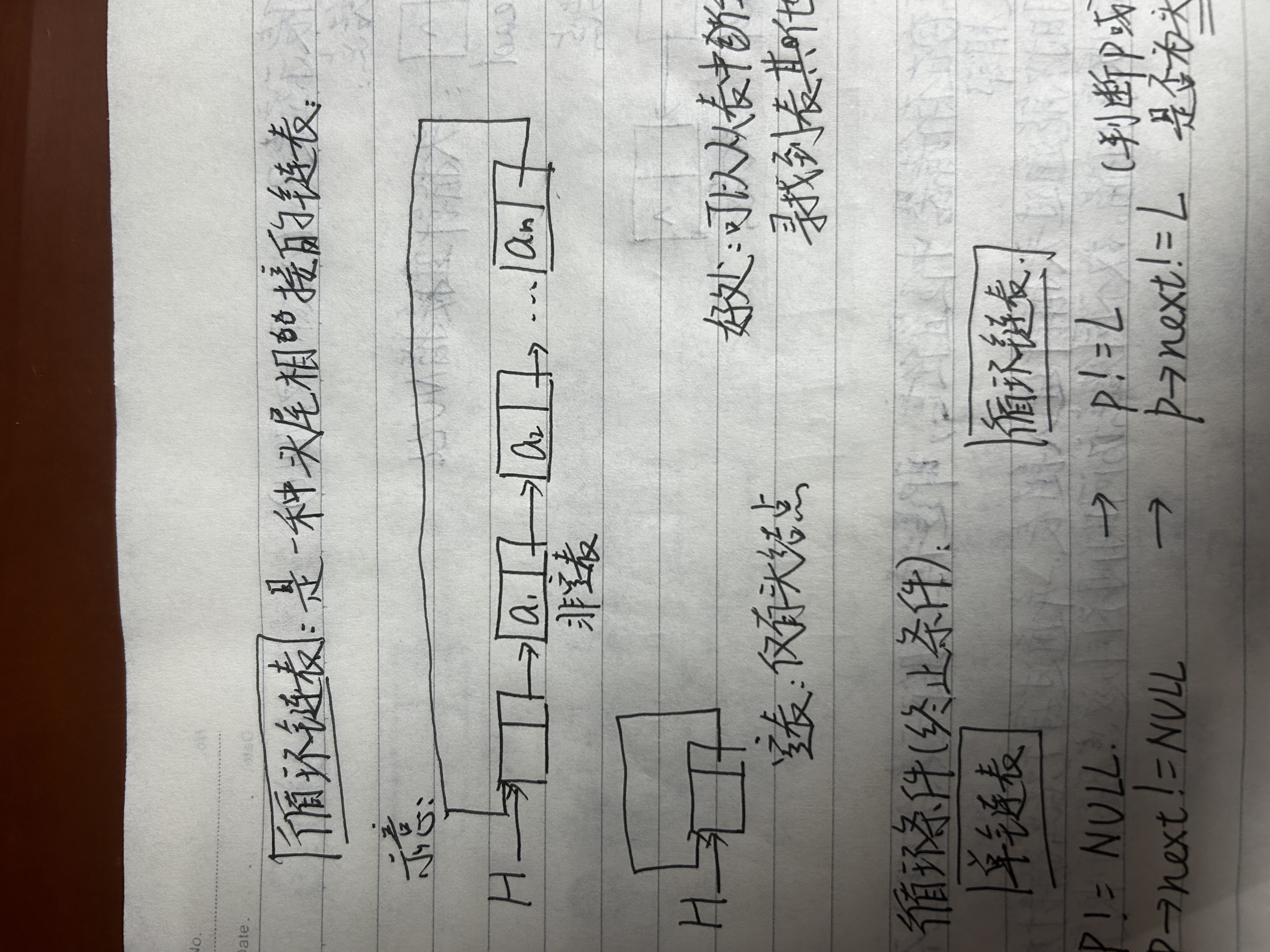
  循环链表将链表尾部重新接到头结点处，这样带来的好处是我们可以从表中任意一处寻找到其他结点而不用非得从头指针开始。

   同时，由于结构上发生的变化，我们常用的一些语句也要跟着变化。

  对于循环链表而言，他的终止条件应该是P！=Head或者P->next！=Head而是NULL

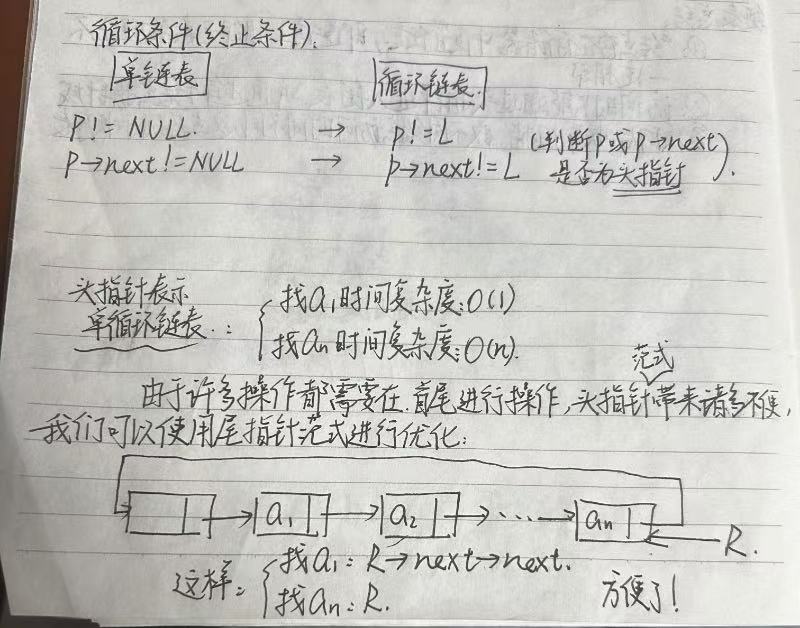
   同时对于链表，我们有许多操作是对头结点或者最后一个结点操作的，我们可以如图采用尾指针范式来表达链表，可以更方便地找到头结点与尾结点。

  直接来看代码：

#include<iostream>
using namespace std;
//循环链表
//定义一个循环链表的节点结构体
typedef struct node
{
    int data; //数据域
    node *next; //指针域
}node, *circular_linklist;

//初始化循环链表
circular_linklist init()
{
    circular_linklist Tail = new node; //创建头节点
    Tail->next = Tail; //尾节点的next指向自己，形成循环链表
    Tail->data = 0; //头节点的数据域初始化为0
    cout << "循环链表初始化成功！" << endl;
    return Tail; //返回头节点
}

//尾插法插入节点
void InsertTail(circular_linklist &Tail, int n)
{
    while(n>0)
    {
        circular_linklist newNode = new node; //创建新节点
        cin >> newNode->data; //输入新节点的数据域
        newNode->next = Tail->next; //新节点的next指向头节点
        Tail->next = newNode; //尾节点的next指向新节点
        Tail = newNode; //更新尾节点为新节点
        n--; //节点数减1
    }
    return; //返回

}

//合并两个循环链表
circular_linklist merge(circular_linklist &Tail1, circular_linklist &Tail2)
{
    circular_linklist p = Tail2->next->next; //获取第二个循环链表的首元结点
    Tail2->next = Tail1->next;//将第二个循环链表指向第一个链表头结点
    Tail1->next = p;//将第一个循环链表尾指针下一位变为第二个首元
    return Tail2; //返回合并后的链表
}

//遍历循环链表并输出节点数据
void traverse(circular_linklist Tail)
{
    circular_linklist p = Tail->next->next; //从头节点开始遍历
    while (p != Tail->next) //直到回到头节点
    {
        cout << p->data << " "; //输出节点数据
        p = p->next; //移动到下一个节点
    }
    cout << endl; //换行
}

int main()
{
    circular_linklist Tail1 = init(); //初始化循环链表
    cout << "请输入第一个循环链表的节点数：";
    int n1;
    cin >> n1; //输入第一个循环链表的节点数
    InsertTail(Tail1, n1); //尾插法插入节点
    cout << "第一个循环链表的节点数据为：";
    traverse(Tail1); //遍历第一个循环链表并输出节点数据

    circular_linklist Tail2 = init(); //初始化第二个循环链表
    cout << "请输入第二个循环链表的节点数：";
    int n2;
    cin >> n2; //输入第二个循环链表的节点数
    InsertTail(Tail2, n2); //尾插法插入节点
    cout << "第二个循环链表的节点数据为：";
    traverse(Tail2); //遍历第二个循环链表并输出节点数据

    circular_linklist TAIL = merge(Tail1, Tail2); //合并两个循环链表
    cout << "合并后的循环链表的节点数据为：";
    traverse(TAIL); //遍历合并后的循环链表并输出节点数据

    return 0; //程序结束
}

2.双向链表

  双向链表的节点中的成员除了next指针，还增加了一个prior指针，这样我们不仅可以“顺藤摸瓜”，沿着next寻找，还可以直接访问节点的前驱，“逆流而上”。

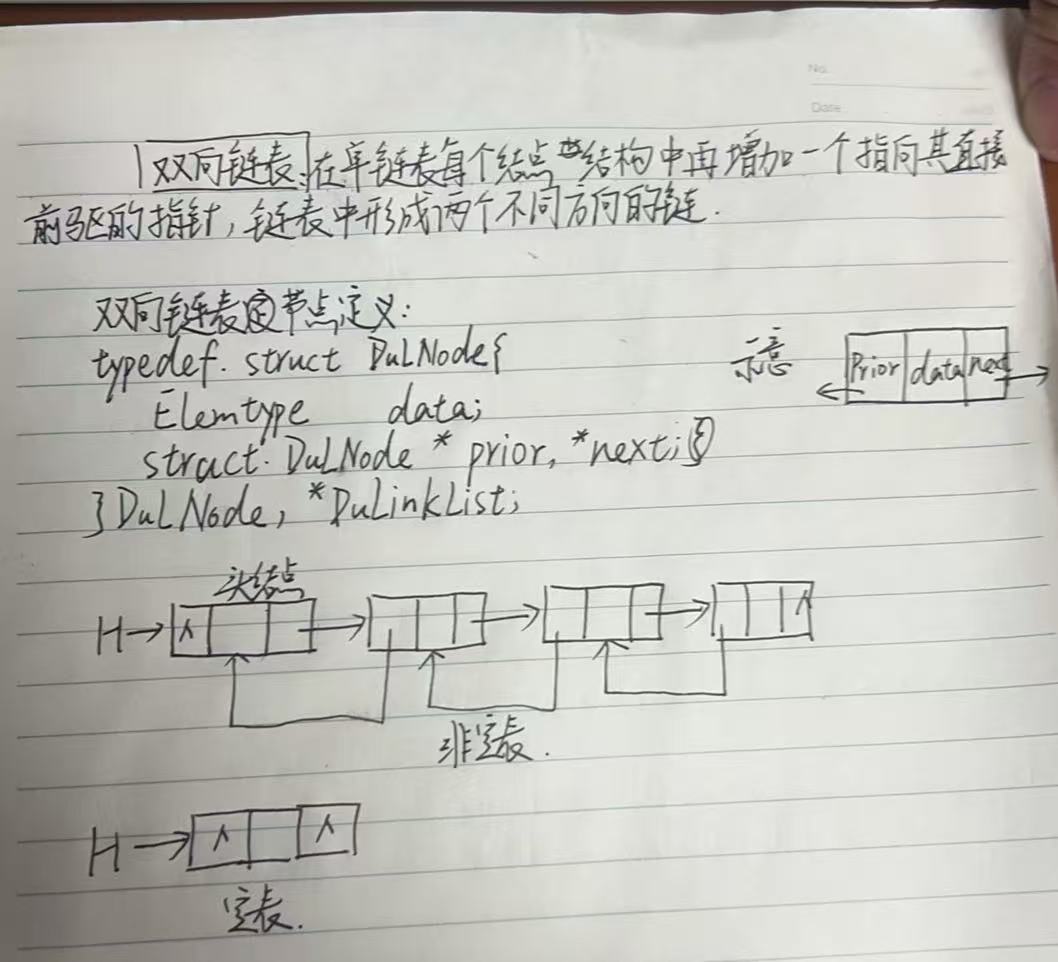
 但是相应的，它的初始化和创建会变得比较复杂。来看代码：

#include<iostream>
using namespace std;
//双向链表
//双向链表结点定义
typedef struct node
{
    int data;
    struct node *prior;
    struct node *next;
}Node,*Double_Linklist;

//初始化双向链表
Double_Linklist init()
{
    Double_Linklist Head = new Node;
    Head->next = NULL;
    Head->prior = NULL;
    cout<<"双向链表初始化成功"<<endl;
    return Head;
}

//头插法完成双向链表创建
void Insert_Head(Double_Linklist &Head ,int n)
{
    while(n>0)
    {
        Double_Linklist newNode = new Node;
        cin>>newNode->data;
        newNode->next = Head->next;
        newNode->prior = Head;
        Head->next = newNode;
        Head->next->prior = newNode;
        newNode->prior = Head;
        n--;
    }
}
//遍历操作
void traverse(Double_Linklist &L)
{
    Double_Linklist p = L->next;//从首元结点开始
    while(p != NULL)
    {
        cout<<p->data<<" ";
        p = p->next;
    }
}


int main()
{
    Double_Linklist L1 = init();
    cout<<"请输入所插入节点个数：";
    int n;
    cin>>n;
    Insert_Head(L1,n);
    traverse(L1);
    return 0; 
}

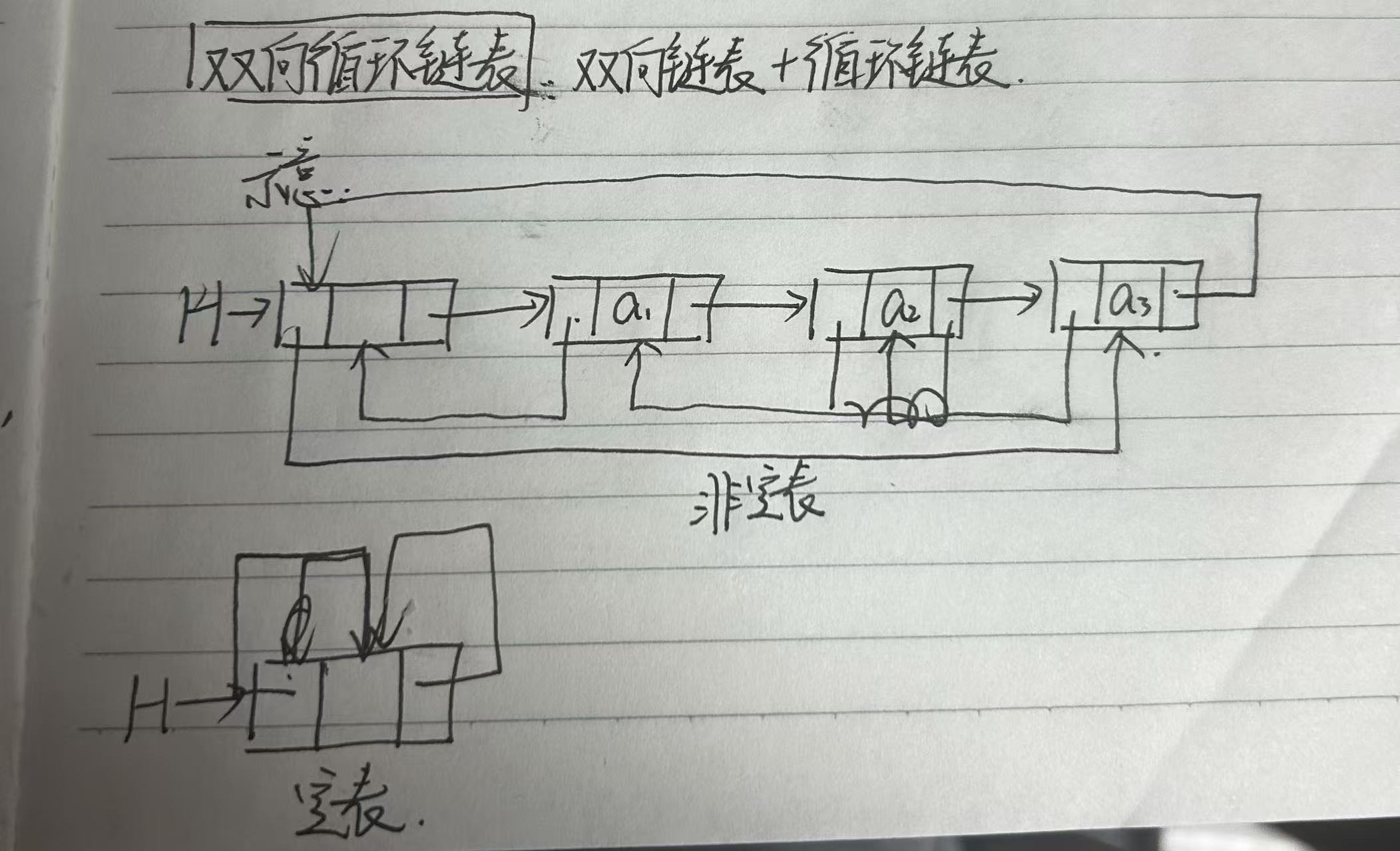
3.双循环链表

  顾名思义，将上述两种机制组合起来，构成了集大成者

#include<iostream>
using namespace std;
//双向循环链表结点定义
typedef struct node
{
    int data;
    struct node *prior;
    struct node *next;
}Node,*Double_Circular_Linklist;

//初始化双向循环链表
Double_Circular_Linklist init()
{
    Double_Circular_Linklist Head = new Node;
    Head->next = Head;
    Head->prior = Head;
    cout<<"双向循环链表初始化成功"<<endl;
    return Head;
}

//头插法完成双向循环链表创建
void Insert_Head(Double_Circular_Linklist &Head ,int n)
{
    Double_Circular_Linklist p = Head;
    for(int i = 0; i < n; i++)
    {
        Double_Circular_Linklist s = new Node;
        cout<<"请输入第"<<i+1<<"个节点的值：";
        cin>>s->data;
        s->next = p->next;//新结点的后继指针指向原链表的第一个结点
        s->prior = p;//新结点的前驱指针指向头结点
        p->next->prior = s;//原链表的第一个结点的前驱指针指向新结点
        p->next = s;//头结点的后继指针指向新结点
    }
}
//遍历操作
void traverse(Double_Circular_Linklist &L)
{
    Double_Circular_Linklist p = L->next;//从首元结点开始
    while(p != L)//循环链表的遍历条件
    {
        cout<<p->data<<" ";
        p = p->next;
    }
}

最后在贴两张对比图，分别是比较了三种不同链表、和比较了顺序表与链表