哈夫曼树（简介）

知识点

        权值：树中节点所代表的数值。

        路径长度：从根到每一个节点的路径长度之和。

        节点的带权路径长度：从根到该节点之间的路径长度与该节点的权值的乘积。

        树的带权路径长度（总码）：树中所有叶子结点的带权路径长度之和。

        哈夫曼树：最优二叉树（带权路径长度最短的树）

        哈夫曼树中权值越大，节点离根越近

（引）

画树规则

1. 将所有的权值放入一个空间中，并按照权值的大小，给它们排序；
2. 从空间中，选择两个权值最小的节点，将这两节点作为左右子树；
3. 计算该子树的权值之和，并将和作为该子树的父结点；
4. 在空间中删除使用的两个权值，并添加这两个权值的和进入空间；
5. 重复整个过程，直到最后只有一个值结束。

 假设有五个节点{a，b，c，d，e}，它们的权值为{9，7，2，5，1}，根据节点画一棵哈夫曼树。

• 先将权值按照从小到大排序：{1，2，5，7，9}
• 选择两个最小的作为左右子树，并计算它们的和作为父节点

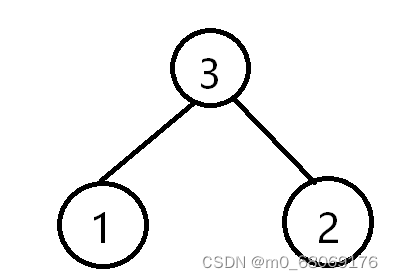
• 删除使用的两个权值，并添加这两个权值的和进入空间，重新排序为 {3，5，7，9}
• 再次选择两个最小的作为左右子树，并计算它们的和作为父节点

  

•  重复整个过程，直到只有一个数值截止，整棵树画完

• 

画树时要注意

• 权值小的节点在左边，权值大的节点在右边
• 当和与节点的权值相等时，节点一般放右边
• 对于根结点而言，左边的分叉数量要小于右边的分叉数量

哈夫曼编码

• 左子树为0，右子树为1
• 读编码的时候，从根结点开始读，直到节点结束
• 注意：
• 没有任何一个节点的编码为1
• 最好没有任何一个节点的编码是另一个节点编码的开头
• 若节点数量为n，则该树所画出来的节点总数为：2n-1

以上题例子为样，各节点的编码为：

总码为：9*1+7*2+5*3+1*4+2*4=50