深度学习-线性回归实现-大学生

深度学习-线性回归实现-大学生

一、实验目的

1）掌握深度学习环境的搭建；
2）掌握深度学习模型的开发步骤；
3）掌握深度学习模型的运行和测试方法；
4）掌握模型的训练方法；

二、实验内容

1）安装深度学习环境管理工具；
2）安装Python深度学习开发IDE并与开发环境进行关联；
3）开发线性回归模型；
4）训练模型并记录训练过程；
5）展示最终训练结果；
6）讨论不同超参数（如：学习率和训练次数）对模型性能的影响；
7）讨论样本大小的必要性，如两个样本能否训练该线性回归模型？若能为什么需要大量样本？若不能给出实验结果并解释？

三、实验结果

1、安装深度学习环境管理工具

（1）、创建虚拟环境pytorch，并激活虚拟环境。如下图片展示了conda environments(虚拟环境)。并顺利激活了虚拟环境。

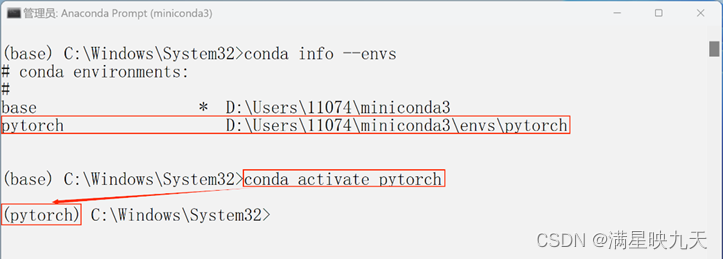
（2）、CUDA安装

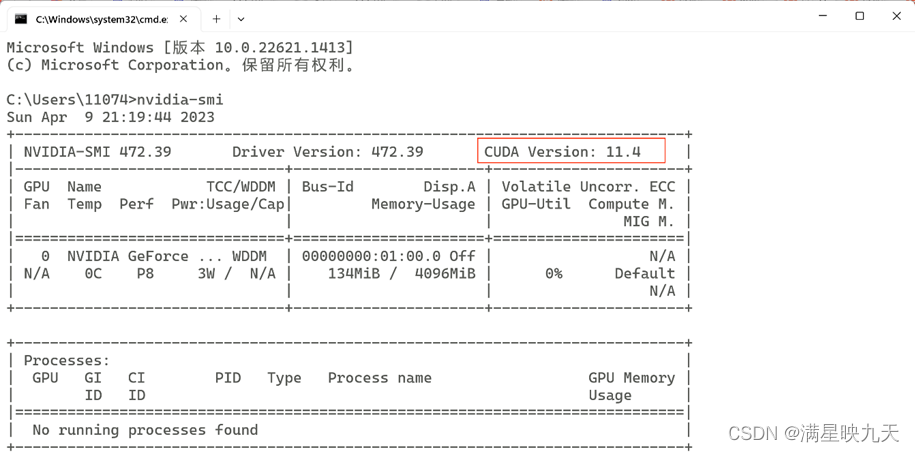
（2）、验证pytorch安装是否成功

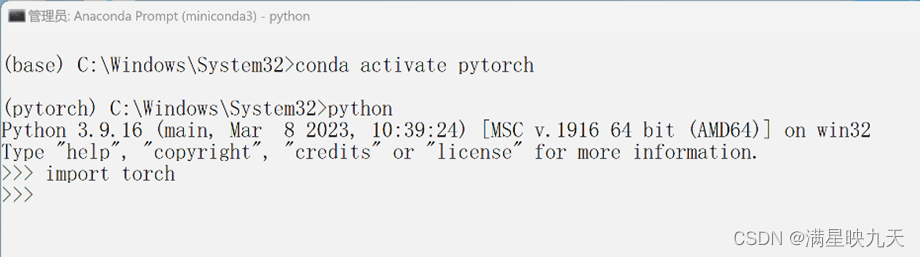
2、安装Python深度学习开发IDE并与开发环境进行关联

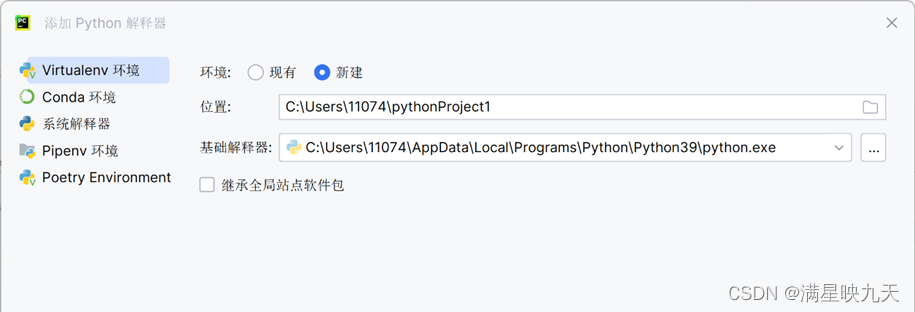
3、线性回归模型代码分析

#使用这两个库可以方便地进行数值计算和数据可视化，是科学计算和数据分析中常用的工具之一。
import numpy as np
import matplotlib.pyplot as plt

#这句代码设置了随机数种子为1，这样每次运行程序生成的随机数都是一样的，保证了结果的可重复性。
np.random.seed(1)

# 生成样本数据
x = np.arange(-1, 1, step=0.02)
noise = np.random.uniform(low=-0.5, high=0.5, size=100)
y = x * (-3) + 2 + noise  # 初始数据

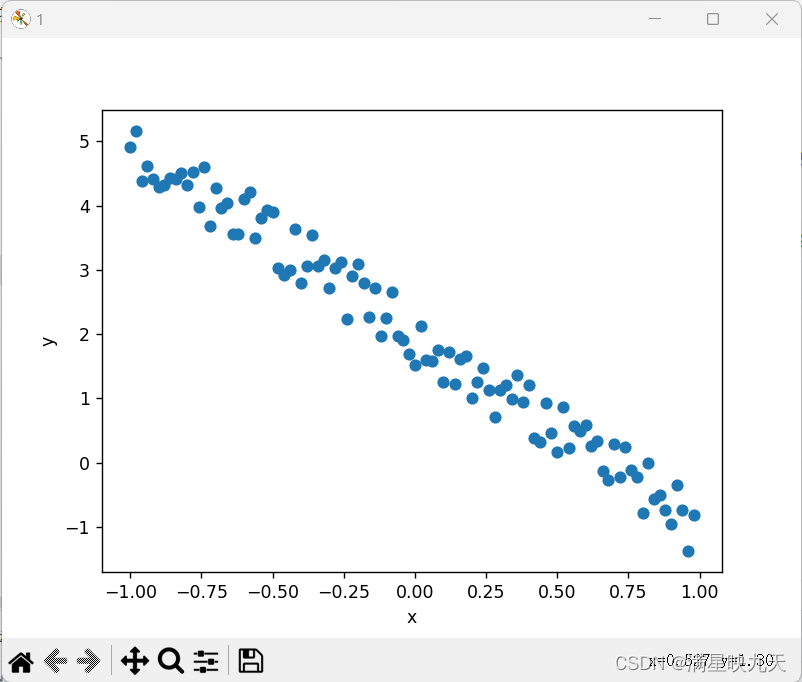
# 显示待拟合数据
plt.figure('1')
plt.xlabel('x')
plt.ylabel('y')
plt.scatter(x, y)

# 损失函数
def cost(theta, k, x, y):
    return np.mean((theta * x + k - y) ** 2)

lr = 0.001   #学习率设置
epoches = 1500  #训练次数
theta = 0  #初始斜率设置
k = 0
acost = []
#迭代更新参数
for i in range(epoches):
    #最速梯度下降
    # theta_gra = 2 * np.mean((theta * x + k - y) * x)
    # k_gra = 2 * np.mean((theta * x + k - y) * x)

    #随机梯度下降
    # np.random.seed(1)
    # pos = np.random.randint(low=1,high=100,size=1)
    # theta_gra=2*np.mean((theta*x[pos]+k-y[pos])*x[pos]) #theta梯度
    # k_gra=2*np.mean(theta*x[pos]+k-y[pos])#k梯度

    #小批量梯度下降
    np.random.seed(1)
    pos = np.random.randint(low=1, high=100, size=10)
    theta_gra = 2 * np.mean((theta * x[pos] + k - y[pos]) * x[pos])  # theta梯度
    k_gra = 2 * np.mean(theta * x[pos] + k - y[pos])  # k梯度

    #更新梯度
    theta -= theta_gra+lr
    k -= k_gra*lr
    rcost = cost(theta,k,x,y)
    acost.append(rcost)
    if i%10==0:
        print("%d:结果为：theta_gra=%f,k_gra=%f,theta=%f,k=%f,Loss=%f"%(i,theta_gra,k_gra,theta,k,rcost))
        py=theta*x+k
        plt.figure('2')
        plt.cla()
        plt.scatter(x,y)
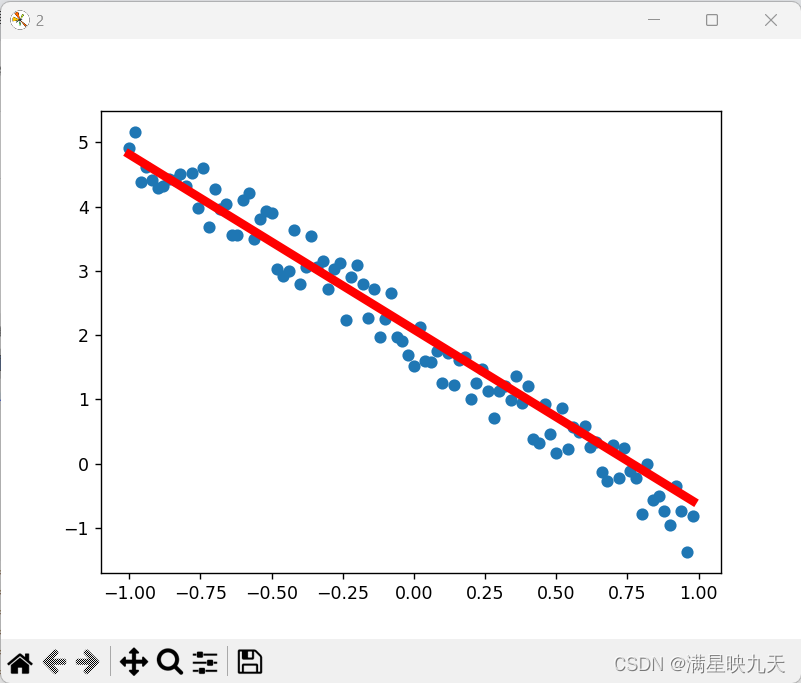
        plt.plot(x,py,'r-',lw=5)
        plt.pause(0.05)
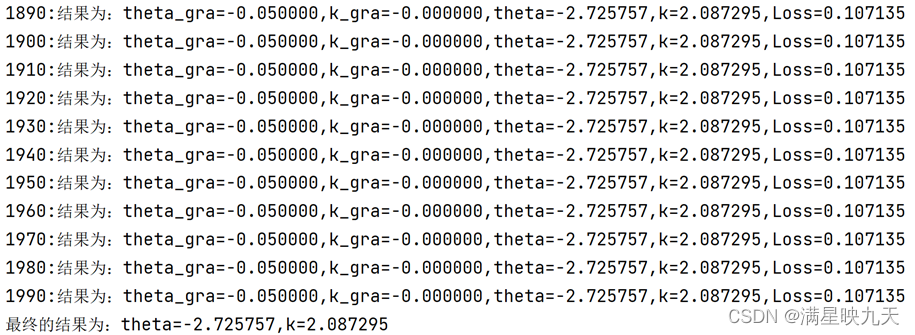
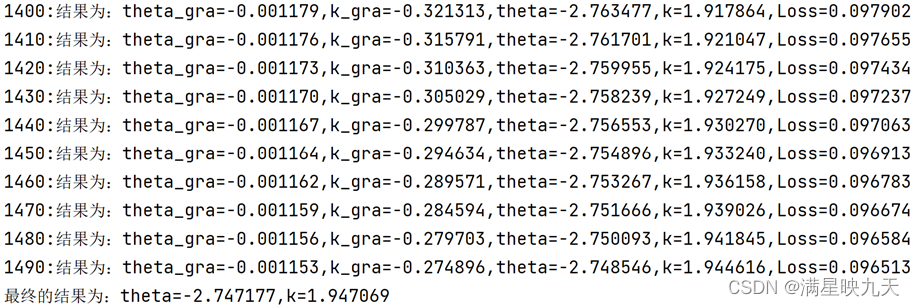
print('最终的结果为：theta=%f,k=%f'%(theta,k))
plt.figure('3')
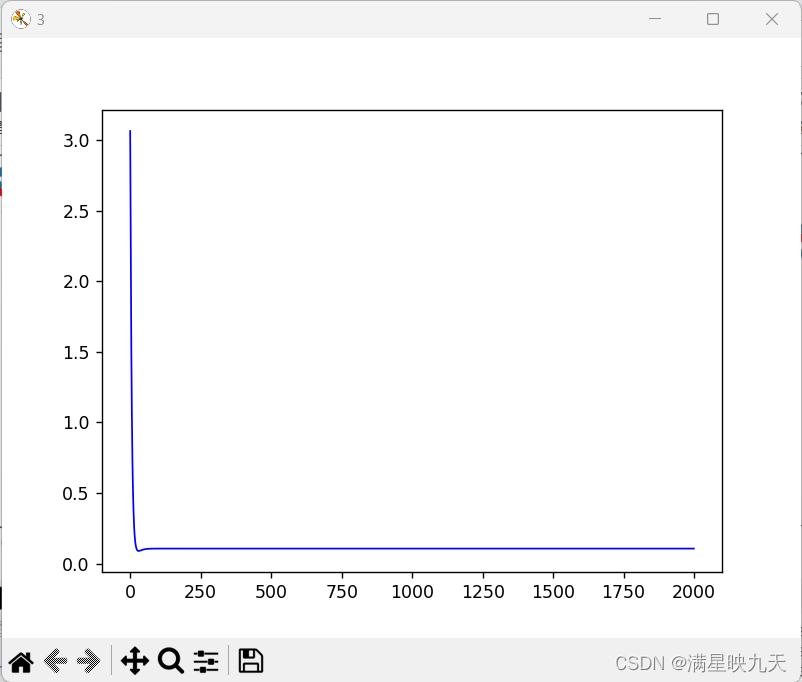
plt.plot(acost,'b-',lw=1)
plt.show()

4、训练模型并记录训练过程

（1）、学习率为0.05，迭代次数为2000次

（2）、学习率为1，迭代次数为2000次

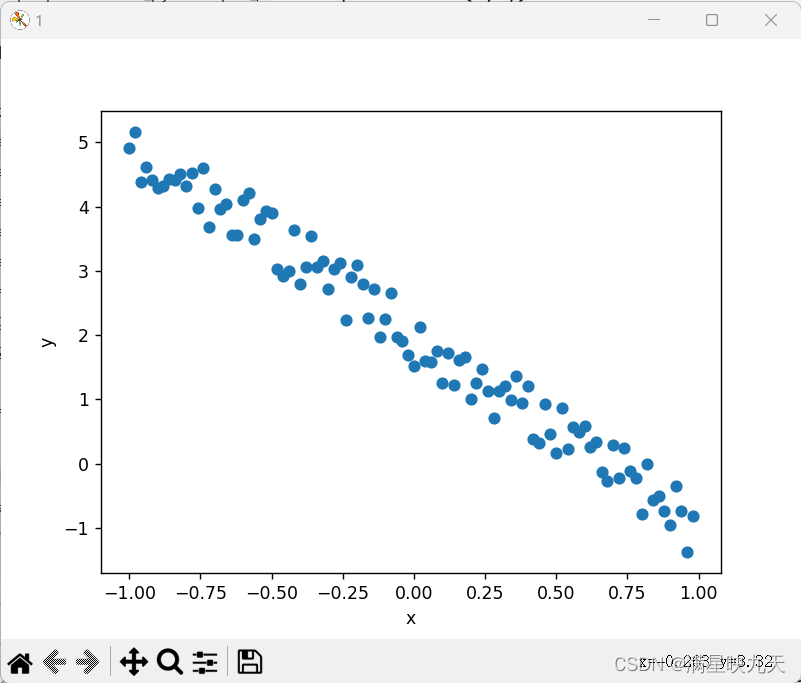
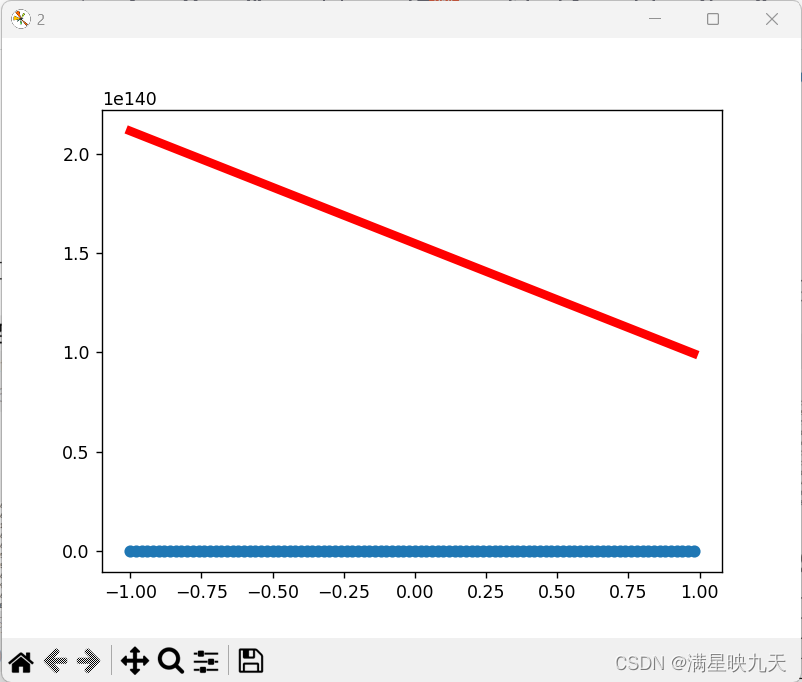
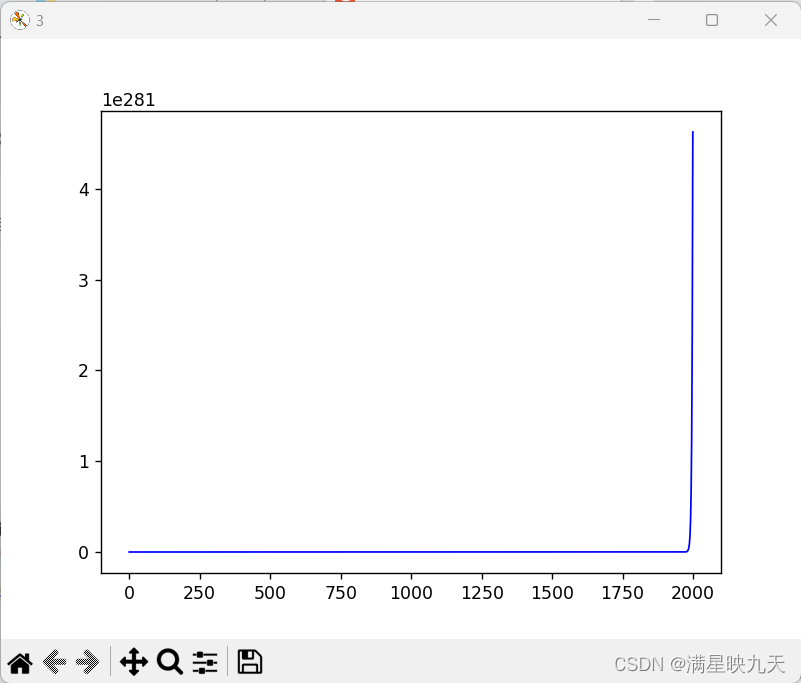
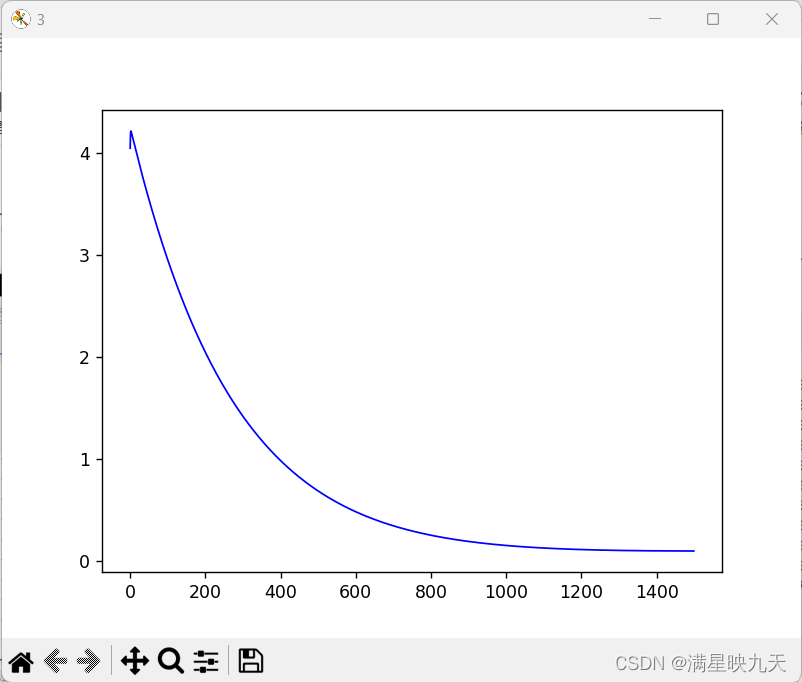
（3）、学习率为0.001，迭代次数为1500次

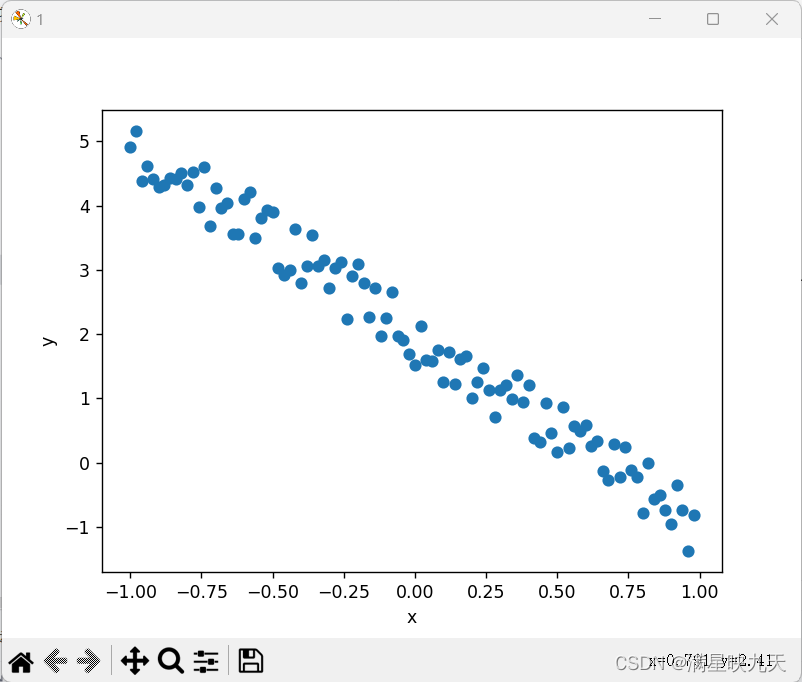
四、实验总结

这段代码实现了使用小批量梯度下降算法对给定的样本数据进行线性回归，并使用matplotlib库对训练过程和结果进行可视化展示。具体来说，代码首先设置了随机数种子，然后生成了样本数据并可视化展示。之后定义了损失函数，并设定了学习率和迭代次数等一些参数。在循环迭代中，每次更新参数采用的是小批量梯度下降算法。更新一定次数后，输出最终的参数和损失，并将损失函数的变化过程显示出来。

学习率影响：学习率决定了模型在每次迭代时更新的步伐大小，如果学习率设置太小，则更新速度缓慢，需要更多的迭代次数才能找到更好的参数；如果学习率设置太大，则可能导致算法无法收敛，甚至会出现震荡现象。因此，学习率的设置需要根据具体的问题进行调整，如果样本数据比较复杂，可以适当提高学习率以加快收敛速度，同时也需要注意不要设置过大。在这段代码中，学习率设置为0.001，随着迭代进行，更新速度逐渐变慢。可能需要根据具体数据或实验进行调整。

迭代次数影响：迭代次数越多，算法找到的参数精度越高，但同时，算法的执行时间也会变长。通常情况下，我们需要在达到一定精度的情况下尽可能减少迭代次数，以便提高算法的效率。但是，如果迭代次数设置太少，则可能会导致算法未能找到合适的参数，从而影响预测结果的准确性。因此，我们需要根据具体情况和经验来设置迭代次数。在这段代码中，迭代次数设置为1500，可以看出随着迭代次数的增加，损失函数逐渐减小，但有时候迭代次数过多也会出现过拟合的情况。

附录：代码详细总结

1、import numpy as np
2、import matplotlib.pyplot as plt
#1-2使用这两个库可以方便地进行数值计算和数据可视化，是科学计算和数据分析中常用的工具之一。

3、np.random.seed(1)
#3这句代码设置了随机数种子为1，这样每次运行程序生成的随机数都是一样的，保证了结果的可重复性。

生成样本数据

4、x = np.arange(-1, 1, step=0.02)
#4创建一个从-1到1（不包括1）的一维数组，步长为0.02。np.arange()函数是NumPy中的一个数组创建函数，它用于创建等差数列数组。参数step表示每个数之间的间隔，默认值为1。因此，这句代码创建的数组包含了从-1开始，每隔0.02一个单位的数值，直到达到1之前的所有数。

5、noise = np.random.uniform(low=-0.5, high=0.5, size=100)
#5使用NumPy中的random模块生成一个包含100个随机浮点数的一维数组，这些随机浮点数的取值范围在-0.5到0.5之间（即low=-0.5, high=0.5），每个随机浮点数的取值是等概率的

6、y = x * (-3) + 2 + noise # 初始散点（nosic属于噪声）

显示待拟合数据

7、plt.figure(1)
8、plt.xlabel(‘x’)
9、plt.ylabel(‘y’)
10、plt.scatter(x, y)
#7.创建一个名为"1"的新图形窗口。
#8-9.在该图形窗口中创建一个散点图，横坐标为x，纵坐标为y。
#10.在散点图上添加横坐标轴标签为"x"，添加纵坐标轴标签为"y"。

损失函数

11、def cost(theta, k, x, y):
12、 return np.mean((theta * x + k - y) ** 2)
#11-12这段代码定义了一个损失函数，用于计算当前theta和k对应的线性回归模型的预测值与实际值之间的平均误差。其中，theta和k是线性回归模型的参数，x和y是原始数据的输入和输出。

13、lr = 0.005 #学习率设置
14、epoches = 2000 #训练次数
15、theta = 0 #初始斜率设置
16、k = 0 #初始偏置设置
17、acost = []
#迭代更新参数
18、for i in range(epoches):
#最速梯度下降
# theta_gra = 2 * np.mean((theta * x + k - y) * x)
# k_gra = 2 * np.mean((theta * x + k - y) * x)

#随机梯度下降
# np.random.seed(1)
# pos = np.random.randint(low=1,high=100,size=1)
# theta_gra=2np.mean((thetax[pos]+k-y[pos])x[pos]) #theta梯度
# k_gra=2np.mean(theta*x[pos]+k-y[pos])#k梯度

#小批量梯度下降
19、 np.random.seed(1) #
#19这句代码设置了随机数种子为1，这样每次运行程序生成的随机数都是一样的，保证了结果的可重复性。

20、 pos = np.random.randint(low=1, high=100, size=10)
#20使用NumPy中的random模块生成一个包含100个随机整数的一维数组，这些随机整数的取值范围在1到100之间（即low=1, high=100），每个随机整数的取值是等概率的

21、 theta_gra = 2 * np.mean((theta * x[pos] + k - y[pos]) * x[pos]) # theta梯度
22、 k_gra = 2 * np.mean(theta * x[pos] + k - y[pos]) # k梯度

23、 theta -= theta_gra+lr
#表示将当前的theta值减去theta的梯度和学习率的加和，得到新的theta值；
24、 k -= k_gralr
#表示将当前的k值减去k的梯度和学习率的乘积，得到新的k值。
25、 rcost = cost(theta,k,x,y)
#将更新的回归参数theta和k重新代入到损失函数中，实现让损失函数不断减小的目标。
26、 acost.append(rcost)
#将每次迭代的损失函数值添加到数列中。
27、 if i%10==0:
#由于将迭代次数设置为2000次，我们每10次展示线性回归模型的拟合效果。
28、print(“%d:结果为：theta_gra=%f,k_gra=%f,theta=%f,k=%f,Loss=%f”%(i,theta_gra,k_gra,theta,k,rcost))
#输出当前的迭代次数，斜率梯度、偏置梯度、斜率、偏置和损失函数值。
29、 py=thetax+k
30、 plt.figure(2)
#表示创建一个新的图形窗口，其中数字2表示窗口的编号
31、 plt.cla()
#表示清除当前窗口中的所有图像
32、 plt.scatter(x,y)
#表示画出样本数据的散点图
33、 plt.plot(x,py,‘r-’,lw=5)
#表示画出当前线性回归模型的拟合曲线，其中"x"表示x轴的取值范围，"py"表示根据当前的theta和k计算出的y轴的取值范围，"r-"表示颜色为红色且使用实线来画线，"lw=5"表示线条的宽度为5个像素
34、 plt.pause(0.05)
#表示暂停一段时间，以便能够看到动态的效果
35、print(‘最终的结果为：theta=%f,k=%f’%(theta,k))
#输出了训练过程中得到的最终结果，即线性回归模型中的斜率(theta)和偏置(k)的值
36、plt.figure(3)
#表示创建一个新的图形窗口，其中数字3表示窗口的编号
37、plt.plot(acost,‘b-’,lw=1)
#实现了将训练过程中的损失函数值(acost)绘制成一条曲线，以便于分析模型拟合效果的好坏
38、plt.show()
#将绘制好的曲线展示在屏幕上