在|z|<1的环域展开
在命令行窗口输入

查看taylor函数文档:https://www.mathworks.com/help/releases/R2021b/symbolic/sym.taylor.html
点击enter键,得到结果:

整理得:
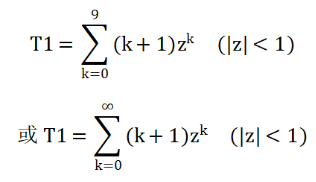
就是函数 1/(1-z)^2 (|z|<1)的级数展开式
在1<|z|<∞的环域展开

命令行窗口输入:

得到结果:
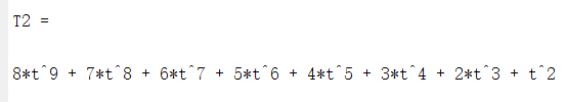
整理得:

就是函数 1/(1-z)^2 (1<|z|<∞)的级数展开式。
绘图
根据上述得到的展开式编写M程序。
在M程序文件(“.m”后缀):
%1/(1-z)^2幂级数展开及绘图表示
m=30;%与图形的平滑度(精度)相关
r=(0:2*m)'/m; %模
theta=pi*(-m:m)/m; %幅角
z=r*exp(1i*theta); %Euler欧拉表示
z(z==1)=NaN;%挖去奇点
f=1./(1-z).^2;
figure(1)%打开图形窗口
cplxmap(z,f); %原函数
colorbar('vert');%此 MATLAB 函数 在当前坐标区或图的右侧显示一个垂直颜色栏
z1=z;
z1(abs(z1)>=1)=NaN; %选定收敛域,|z|<1
f1=1;%通项和
u1=1;%通项次幂
for k=1:100%for循环,求101个项数的和
u1=u1.*z1;%累乘得到下一个高次幂(不含系数)
f1=f1+(k+1).*u1;%累加求和,逼近原函数
end
figure(2)%打开图形窗口
subplot(1,2,1);%在各个分块位置创建坐标区
cplxmap(z1,f1);%Taylor,绘制一个复变量的函数
z2=z;
z2(abs(z2)<=1)=NaN; %选定收敛域,|z|>1
f2=1./z2.^2;%通项和
u2=1./z2.^2;%通项次幂
for k=1:100%for循环,求101个项数的和
u2=u2./z2;%累除得到下一个高次幂(不含系数)
f2=f2+(k+1).*u2;%累加求和,逼近原函数
end
figure(2)%打开图形窗口
subplot(1,2,2);%在各个分块位置创建坐标区
cplxmap(z2,f2);%Lauren,洛朗展开运行得到输出图形:

原函数的图像

展开式图像:在|z|<1的环域展开(左),在1<|z|<∞的环域展开(右,部分)

在工作区查看原函数和展开式的部分值并对比,分别点击f,f1,f2

f= 1/(1-z)^2

在|z|<1的环域展开,与上图一致
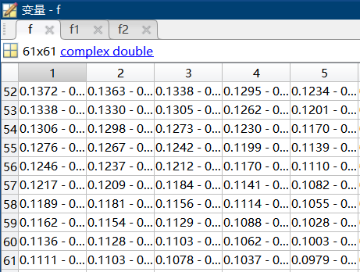
f= 1/(1-z)^2

在1<|z|<∞的环域展开,与上图一致
结束语
本文是作者第一篇文章,末流985大二学生的一次作业分享,希望得到大家的认同,如有错误或更好的解决办法,欢迎在评论区交流Thanks♪(・ω・)ノ。
我曾到CSDN上找相关文章完成作业,但是没找到自己想要的,完成以后想着帮到其他有需要的人。
可能有些步骤细节没有展示,有不懂的可以私信。



























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










