《学生信息管理系统》链式存储结构实现

一、需求分析

系统名称为：学生信息管理系统。它包括了浏览、插入、删除、查找以及修改学生信息的功能。

二、概要设计

1、主程序的流程说明

在主函数中，运用单链表和结构体来实现，学生信息管理系统的浏览、插入、删除、查找以及修改学生信息的功能。

2.程序中用到的数据逻辑结构描述及其上定义的函数的描述

   （1）数据结构  

线性表的线性结构觉决定了它的性质：数据元素之间是一种线性关系，数据元素一个接一个的排列，除了最后一个数据，其他的数据面临的下一个数据有且仅有一个。

(2)存储结构

单链表采用一个结点存放一个数据元素，每个结点除了包括存放数据                                           元素值的数据域外，还包括指向下一个元素的存储位置的next指针域。最后一  个结点的指针域为空。

3、存储表示

//学生结构体类型定义
typedef struct
{
	char sno[14];	
	char sname[7];
	char sex[3];		
	int  score;			 
}student;
typedef student ElemType;   /*定义元素类型为student*/
//单链表类型定义（单链表存储表示）
typedef struct LNode
{
	ElemType data;
	struct LNode *next;
}LNode,*LinkList;
//LinkList p头指针；LNode *p指向头结点指针 
//各个功能函数
//浏览
void PrintList(LinkList L)
{
	LNode *p;
	p=L->next;
if(p==NULL)
{
printf("当前表为空!\n");
}
else
{
	printf("*****************学生信息*****************\n");
	printf("学号\t\t\t姓名\t\t性别\t\t成绩\n"); 
while(p)
{
	printf("%s\t\t%s\t\t%s\t\t%d\n",p->data.sno,p->data.sname,p->data.sex,p->data.score);
	p=p->next;
}
}
}/*在表中第i位置插入元素*/
int Insert_LinkList(LinkList L,int i,ElemType e)
{
	LNode *p,*s;
	int j;
	p=L;j=-1;
	while(p && j<i-1)
	{
	p=p->next;j++;}
	if(!p||j>i-1)
	return 0;//位置不合法
	s=(LNode*)malloc(sizeof(LNode));
	s->data=e;
	s->next=p->next;
	p->next=s;
	return 1; 
}
/*单链表中删除第i个元素*/
int Delete_LinkList(LinkList L,int i,ElemType *e)
{
	LNode *p,*q;
	int j;
	p=L;j=-1;
	while(p->next&& j<i-1)
	{
	p=p->next;j++;}
	if(!(p->next)||j>i-1)
	return 0;//位置不合法
	q=p->next;
	*e=q->data;
	p->next=q->next;free(q);
	return 1; 
}
//查找
LinkList Locate_LinkElem(LinkList L,char key[7])
{
	LinkList p;
	p=L;
	while(p!=NULL&& strcmp(p->data.sname,key)!=0)
	{p=p->next;
	}
	return p;
}

三、详细设计

1. 各功能模块设计
   1）初始化
   功能分析
   为链表表分配一个预定义大小的数组空间。
   代码实现case语句

   //单链表初始化（带头结点）
   LinkList Init_LinkList(LinkList L)
   {
       L=(LNode*)malloc(sizeof(LNode));
       if(!L) return 0;
   L->next=NULL;
   return L;
   }

2. 浏览

功能分析

   在主函数中通过对查看函数的调用来实现学生信息的显示。首先定义一个查看学生信息的函数 PrintList(LinkList L)，通过判断p的值，用printf语句输出学生信息。当p等于空时“当前为空表!”，当p不等于空时输出学生信息。
流程图

流程图1

代码实现case语句

case 1:printf("\n此功能可以浏览学生信息\n\n");
						PrintList(LL);
				            system("pause");break;

3）插入

功能分析

插入功能分析：插入一个节点的关键是要给出插入的位置，不论是什么情况都要先找到一个节点的地址，该节点的可能是查找表中的第i个节点，也可能是查找表中元素值为某一特定值的节点。

流程图

 

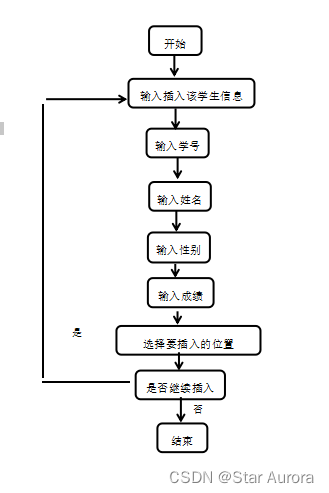
流程图2

代码实现case语句

 case 2:printf("\n此功能可以插入学生信息\n\n");
					 printf("请输入插入该学生的信息；\n");
					 p=1;
					 while(p==1)
					 {
					 	printf("请输入插入该学生学号；\n");  scanf("%s",x.sno);
					 	printf("请输入插入该学生姓名；\n");  scanf("%s",x.sname);
					 	printf("请输入插入该学生性别；\n");  scanf("%s",x.sex);
					 	printf("请输入插入该学生成绩；\n");  scanf("%d",&x.score);
					 	printf("请输入将学生插入到的位置(从0开始):  \n");
					 	scanf("%d",&i);
					 Insert_LinkList(LL,i,x);
						printf("是否继续输入（1表示继续插入，0表示终止插入）:");
						scanf("%d",&p); 
					 }printf("终止信息插入；\n");
					 system("pause");break;

4）删除

功能分析
删除单链表的第i个节点p，将删除位置之前的节点q（即第i-1个节点）的指针指向第i+1个节点，然后释放该节点所占用的存储空间。

流程图

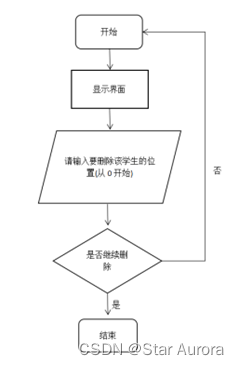
流程图3

代码实现case语句

 case 3:printf("\n此功能可以删除学生信息\n\n");
					 p=1;
					 while(p==1)
					 {  printf("请输入要删除该学生的位置(从0开始)；\n");
					 scanf("%d",&i);
					 Delete_LinkList(LL,i,&x);
						printf("是否继续删除（1表示继续删除，0表示终止删除）:");
						scanf("%d",&p); 
					    Delete_LinkList(LL,i,&x);
					 }printf("终止信息删除；\n");
					 system("pause");break;

5）查找

功能分析
从单链表的最前面的节点开始，判断当前节点是否为第i个节点，若是则返回该节点的地址指针，否则沿着指针域的指向依次向下寻找，直至表结束为止。

流程图

流程图4

代码实现case语句

 case 4:printf("\n此功能可以查找学生信息\n\n");
					 printf("请输入查找学生的姓名；\n");
					 scanf("%s",key);
					m=Locate_LinkElem(LL,key);
					if(m!=NULL)
					printf("学号\t\t姓名\t\t性别\t\t成绩\n"); 
					printf("%s\t\t%s\t\t%s\t%d\n",m->data.sno,m->data.sname,m->data.sex,m->data.score);
					 system("pause");break;

6）修改

功能分析

先输入要修改学生的姓名，在显示学生信息的界面进行学生信息的修改，最后选择是否继续，否的话退回到主界面。

流程图

流程图5

代码实现case语句

 case 5:printf("\n此功能可以修改学生信息\n\n");
					p=1;
					while(p)
					{
					 printf("请输入修改学生的姓名；\n");
					  scanf("%s",key);
					 m=Locate_LinkElem(LL,key); 
					 printf("学号\t\t姓名\t\t性别\t\t成绩\n"); 
					printf("%s\t\t%s\t\t%s\t%d\n",m->data.sno,m->data.sname,m->data.sex,m->data.score);
					printf("请确认是否对信息进行修改 yes(1)；\n");
					scanf("%d",&i);
					if(i==1)
					{
						printf("请输入修改该学生学号；\n");  scanf("%s",m->data.sno);
					 	printf("请输入修改该学生姓名；\n");  scanf("%s",m->data.sname);
					 	printf("请输入修改该学生性别；\n");  scanf("%s",m->data.sex);
					 	printf("请输入修改该学生成绩；\n");  scanf("%d",&m->data.score);	
					}
					else
					printf("查无此人");
					printf("是否继续对信息进行修改 yes(1)no(0)；\n");
					scanf("%d",&p);
					}
					 system("pause");break;

四、调试分析

1.问题与对策
（1）问题：代码编译没有显示错误，但是插入成功后不能正常使用浏览功能

对策：将while语句的判断条件改为j<i-1。

2.基本操作的算法复杂度分析

（1）浏览的算法复杂度分析

单链表的优点就是快速存取，它的时间复杂度为O（1)。

（2）插入的算法复杂度分析

由于查找任何一个节点的平均时间复杂度都是O（n），因此查找某个节点或者它的前驱节点的平均时间复杂度也都是O（n）。因此在不知道节点及其前驱节点的地址的情况下，插入一个节点的时间复杂度为O（n），但如果已知相邻节点的情况下，时间复杂度是O(1)。

（3）删除的算法复杂度分析

如若知道要删除的节点和它的前驱节点的地址的情况下，由于删除时不需要移动元素，所以，删除一个节点的时间复杂度为O(1)。