递推1~8（1238.统计每个月兔子的总数、1146.求S的值、1147.求1/1+…的前n项的和、1145 数列求和、1082.猴子吃桃子、1148.数小木块、1216.数塔问题、1224.过河卒）

题单地址：题单中心-东方博宜OJ

1238. 统计每个月兔子的总数

问题描述

有一对兔子，从出生后第 3 个月起每个月都生一对兔子，一对小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死。问第 n 个月（ n ≤ 50 ）的兔子总数为多少对？

输入 1 个整数 n ，表示第几个月。第 n 个月兔子的总数量有多少对？

样例

输入

9

输出

34

解析：经典斐波那契数列，递推式：a(n) = a(n-1) + a(n-2)

#include <bits/stdc++.h>
using namespace std;

long long a[55] = {0, 1, 1};

int main(){
	int n;
	cin >> n;
	for(int i = 3; i <= n; i++){
		a[i] = a[i-1] + a[i-2];
	}
	cout << a[n] << endl;
	return 0;
}  

---

1146. 求S的值

问题描述

求 S = 1 + 2 + 4 + 7 + 11 + 16… 的值刚好大于等于 5000 时 S 的值。

输入

无

输出

一行，一个整数。

解析：每一项都是前一项加上序号。

#include <bits/stdc++.h>
using namespace std;

int main(){
	int i = 1, sum = 0, ans = 1;
	while(sum < 5000){
		sum += ans;
		ans += i;
		i++;
	}
	cout << sum;
	return 0;
}  

---

1147. 求1/1+1/2+2/3+3/5+5/8+8/13+13/21……的前n项的和

问题描述

求1/1+1/2+2/3+3/5+5/8+8/13+13/21+21/34…的前 n 项的和。

输入

输入一个整数 n（1 ≤ n ≤ 30）。

输出

输出一个小数，即前 n 项之和（保留 3 位小数）。

样例

输入

20

输出

12.660

解析：通过观察得出公式里的数字符合斐波那契数列，先求数列再根据公式计算。

#include<bits/stdc++.h>
using namespace std;

int main(){
	int n, a[35] = {0, 1, 1};
	double sum = 0;
	cin >> n;
	for(int i = 3; i <= n+1; i++){
		a[i] = a[i-1] + a[i-2];
	}
	for(int i = 1; i <= n; i++){
		sum += (a[i] * 1.0) / (a[i+1] * 1.0); 
	}
	printf("%.3lf", sum);
	return 0;
}

---

1145. 数列求和

问题描述

有一数列如下： 1 2 4 7 11 16 22 …… 试求该数列前 N 项之和。

输入

一个整数 N （ 0 < N < 1000 ）。

输出

一个整数。

样例

输入

6

输出

41

解析：每一项都是前一项加上序号。

#include<bits/stdc++.h>
using namespace std;


int main(){
	int n, ans = 1, sum = 0;
	cin >> n;
	for(int i = 1; i <= n; i++){
		sum += ans;
		ans += i;
	}
	cout << sum;
	return 0;
}

---

1082. 猴子吃桃子

问题描述

猴子吃桃子问题：猴子第一天摘下若干个桃子，当即吃了一半还不过瘾，又多吃了一个；第二天又将剩下的桃子吃掉一半又多吃了一个；以后每天早上都吃了前一天剩下的一半零一个。到了第十天想再吃时，见只剩下一个桃子，求第一天共摘了多少个桃子？

输出

一个整数，第一天共有多少个桃子。

解析：每一次都是吃掉 n / 2 - 1 个桃子，所以逆向推导，手上的桃子加1再乘2等于吃之前的桃子。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int n, conut = 0;
	n = 1;
	for(int i = 10; i > 1; i--){
		n = (n + 1) * 2;
	}
	cout << n;
	return 0;
}

---

1148. 数数小木块

问题描述

在墙角堆放着一堆完全相同的正方体小木块，如下图所示：

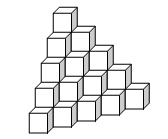
因为木块堆得实在是太有规律了，你只要知道它的层数就可以计算所有木块的数量了。

输入

只有一个整数 n ，表示这堆小木块的层数，已知 1 ≤ n ≤ 100。

输出

只有一个整数，表示这堆小木块的总数量。

样例

输入

5

输出

35

解析：从上往下，每一层木块数量等于上一层木块数量加上当前层数。初始化第一层木块数量为1。

#include<bits/stdc++.h>
using namespace std;


int main(){
	int n, ans = 1, sum = 1;
	cin >> n;
	for(int i = 2; i <= n; i++){
		ans += i;
		sum += ans;
	}
	cout << sum;
	return 0;
}

---

1216. 数塔问题

问题描述

有如下所示的数塔，要求从底层走到顶层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

输入

输入数据首先包括一个整数整数 N (1 ≤ N ≤ 100)，表示数塔的高度，接下来用 N 行数字表示数塔，其中第 i 行有个 i 个整数，且所有的整数均在区间 [0, 99] 内。

输出

从底层走到顶层经过的数字的最大和是多少？

样例

输入

5

7

3 8

8 1 0

2 7 4 4

4 5 2 6 5

输出

30

解析：从倒数第二行开始往上递推，每次选择正下方和右下方值最大的数。答案在a[1][1]。

#include<bits/stdc++.h>
using namespace std;

int main() {
	int n, a[105][105];
	cin >> n;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= i; j++){
			cin >> a[i][j];
		}
	}
	for(int i = n-1; i >= 0; i--){
		for(int j = 1; j <= i; j++){
			a[i][j] += max(a[i+1][j], a[i+1][j+1]);
		}
	}
	cout << a[1][1];
	return 0;
}

---

1224. 过河卒

问题描述

A 点有一个过河卒，需要走到目标 B 点。

卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如下图的 C 点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。

例如：下图 C 点可以控制 9 个点（图中的 P1, P2…P8 和 C ），卒不能通过对方马的控制点。 棋盘用坐标表示，现给定 AA 点位置为 (0, 0)， B 点位置为 (n, m) (n, m 为不超过 20 的整数)，马的位置 C 为 (X, Y)（约定: C 点与 A 点不重叠，与 B 点也不重叠）。

要求你计算出卒从 A 点能够到达 B 点的路径的条数。

输入

B 点的坐标 (n, m) 以及对方马的坐标 (X, Y)；（马的坐标一定在棋盘范围内，但要注意，可能落在边界的轴上）

输出

输出卒从 A 点能够到达 B 点的路径条数。（本题的路径条数可能会超过 10^9，但不会超过 10^18，C/C++选手请注意使用long long）

样例

输入

6 6 3 2

输出

17

解析：在二维数组上标记出马和马的控制点，由于只能向右和向下走，所以每一个点的方案数都来自于它的左边和上边。答案在a[n][m]。

#include<bits/stdc++.h>
using namespace std;

int main() {
	long long a[40][40], n, m, x, y;
	bool s[40][40];
	int v[10][2] = {{0, 0}, {2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
	cin >> n >> m >> x >> y;
	n += 2, m += 2, x += 2, y += 2;
	memset(a, 0, sizeof(a));
	memset(s, 0, sizeof(s));
	a[2][1] = 1;
	s[x][y] = 1;
	for(int i = 1; i <= 8; i++) s[x + v[i][0]][y + v[i][1]] = 1;
	for(int i = 2; i <= n; i++){
		for(int j = 2; j <= m; j++){
			if(s[i][j])continue;
			a[i][j] = a[i-1][j] + a[i][j-1];
		}
	}
	cout << a[n][m];
	return 0;
}