数学不好,真不好。
等腰三角形的存在性问题
有两定点A,B,求一点C,使得为等腰三角形。
几何方法
分三种情况。
- 以A为顶点,AB为腰:以A为圆心,AB为半径的圆上,除过线段AB的点以外都是C的解。(图上红色的部分)
- 以A为顶点,AB为腰:以A为圆心,AB为半径的圆上,除过线段AB的点以外都是C的解。(图上蓝色的部分)
- 以C为顶点,AB为底:作AB的中垂线,除过线段AB的点以外都是C的解。(图上绿色的部分)
综上,C的解集为:

红+蓝+绿(不在AB上的部分)。
求解方法
两点之间距离公式。(两等边等长)
(勾股定理)
(为方便计算)
一样的,红、蓝、绿三类解分三种情况讨论。
设在中,
。
AB=AC(红色)
;
AB=BC(蓝色)
;
AC=BC(绿色)
;
直角三角形的存在性问题
几何方法
有两定点A,B,求一点C,使得为直角三角形。
:过A点
AB的直线。(红)
:过B点
AB的直线。(蓝)
:以AB为直径的圆。(绿)

解集:红+蓝+绿(不在直线AB上的部分)
求解方法
垂直斜率乘积为-1。
(斜率公式)
设在中,
。
AB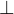 AC(红)
AC(红)
AB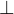 BC(蓝)
BC(蓝)
AC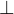 BC(绿)
BC(绿)
等腰直角三角形的存在性问题
因为不常考,就不详细讲了。
一共六个解。
几何方法


求解方法
联立对应的两个前文所述方程即可。
我的第二篇whk博客!
稍后会更新四边形存在性问题哦!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








