北航线性系统-高庆

csholic

于 2024-11-26 17:04:09 发布

阅读量336

点赞数 3

文章标签：算法

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_69709166/article/details/144060233

版权

今天记录13周高庆老师的线性系统课程

每次开始前都先讲解上周题目

1.题目

题目后面补充

1.1

1.2

2.课程

2.1 Schur complement

2.2 T-S模糊模型

2.3 D-T T-S 模糊模型

$x(k+1)=\sum \mu_{i}(x(k))A_{i}x(k)+Bu(k)$

当

$u(k)=kx(k)$

原式为

$x(k+1)=\sum \mu_{i}(x(k))(A_{i}+Bk)x(k)$

$V(x)=x^{T}Px$

$V(x(k+1))-V(x(k))<0$

$(A_{i}+Bk)^{T}P(A+B_{i}k)-P<0$

$Q(A_{i}+Bk)^{T}Q^{-1}(A_{i}+Bk)-Q<0$

$\begin{bmatrix} Q&Q ( A_{i}+ Bk_{i})^{T} \\ ( A_{i}+ Bk_{i})Q& Q \end{bmatrix}>0$

当

$u(k)=\sum \mu_{i}(k) k_{i}x(k)$

原式为

$x(k+1)=\sum \mu_{i}(A_{i}+Bk_{i})x(k_{i})$

运算和上面类似，最后得到

$\begin{bmatrix} Q&* \\ ( A_{i}+ Bk_{i})Q& Q \end{bmatrix}>0$

当...

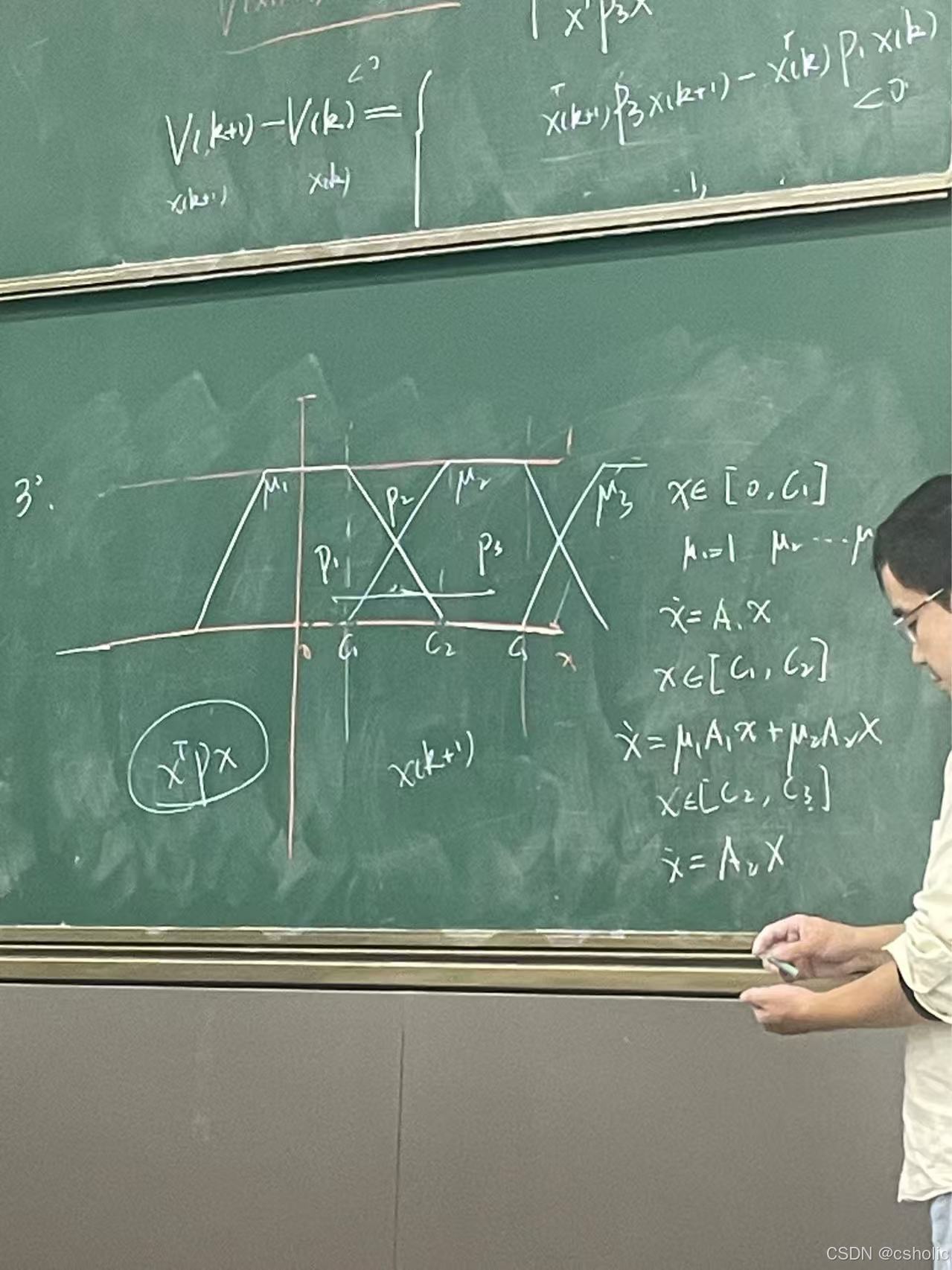
老师画的图没懂，后面再来补充，这里用到2.4Lyapunox函数

当

同样也不知道老师在说什么，后面懂了再来补充

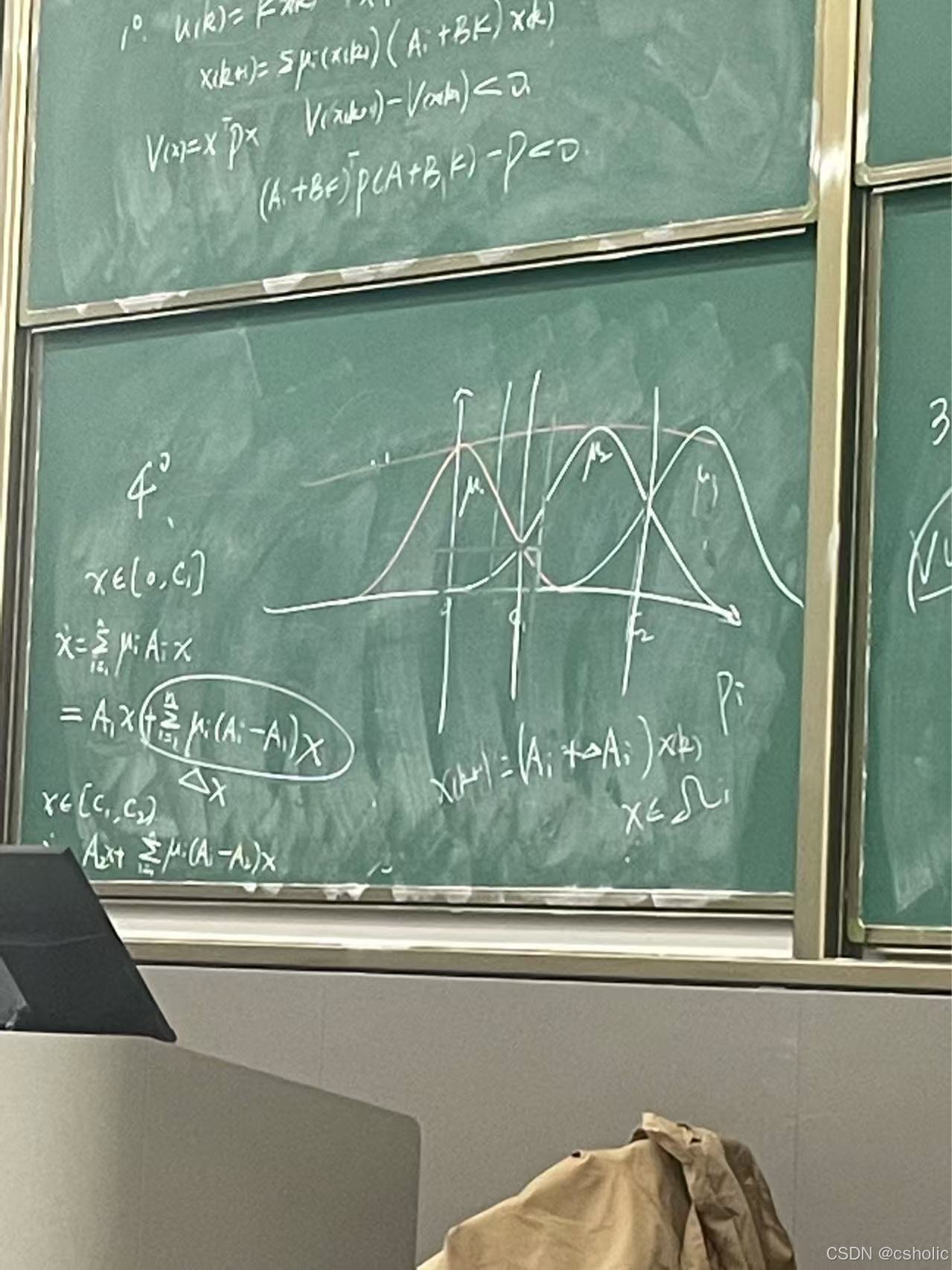
2.4 Lyapunox函数

$V(x)=\left\{\begin{matrix} x^{T}p_{1}x ...& x^{T}p_{2}x... & x^{T}p_{3}x ...\end{matrix}\right.$

$V(k+1)-V(k)=\left\{\begin{matrix} ...&... &... \end{matrix}\right.$

2.5 不确定性系统

$x(k+1)=(A+\Delta A)x+(B+\Delta B)u$

$\dot{x}(t)=(A+\Delta A)x(t)+Bu(t)$

$u(t)=kx(t)$

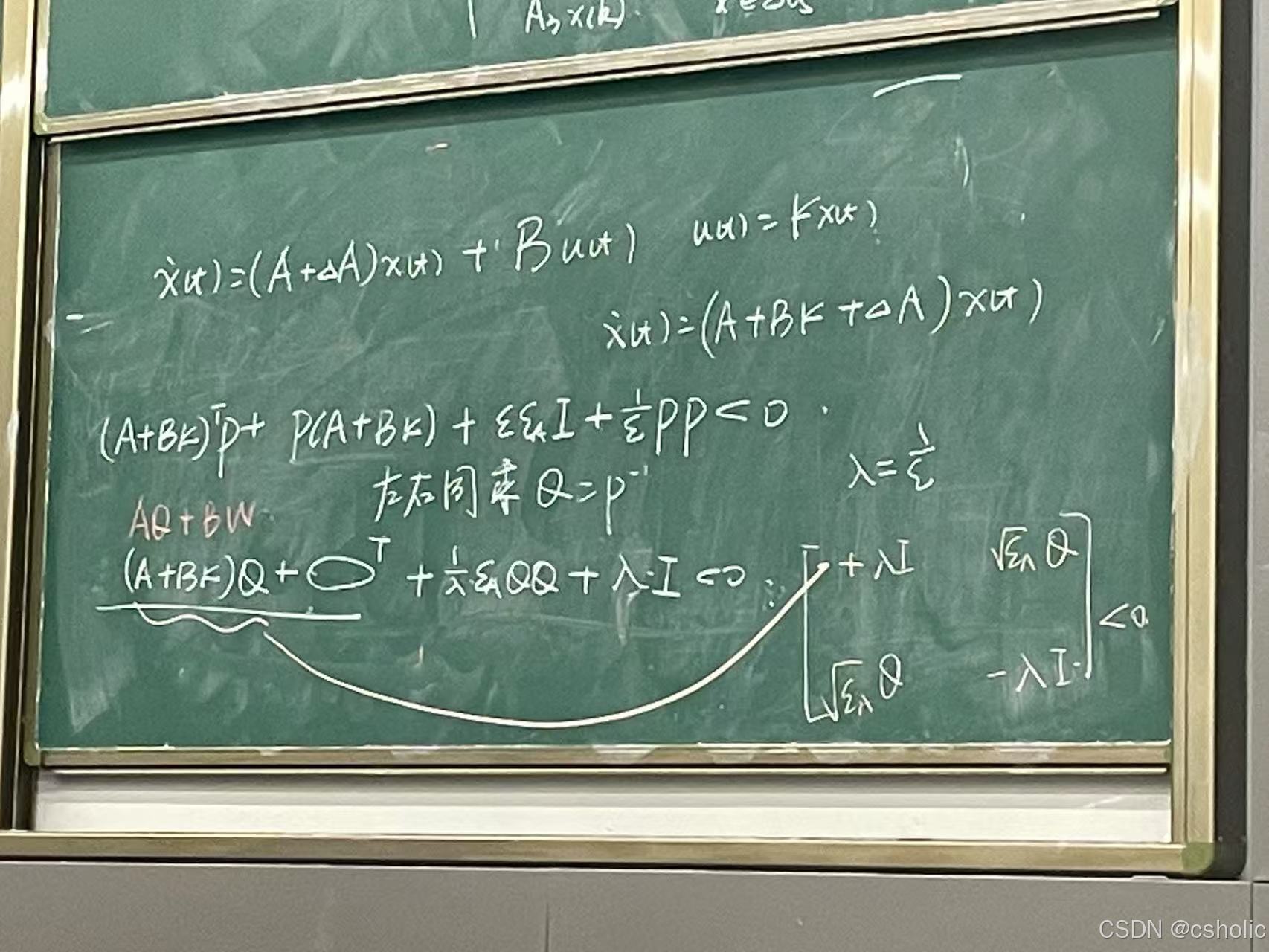
3.下周的作业

3.1

假设

$x(k+1)=\sum \mu _{i}A_{i}x(k_{i})$

可以分段描述为

$x(k+1)=\left\{\begin{matrix} A_{1}x(k) x\in \Omega _{1}&\mu _{1}A_{1}x(k)+\mu _{2}A_{2}x(k) x\in \Omega _{2} &A_{3}x(k) x\in \Omega _{3} &\mu _{2}A_{2}x(k)+\mu _{3}A_{3}x(k) x\in \Omega _{4} & A_{5}x(k) x\in \Omega _{5} \end{matrix}\right.$

选择Lyapunox函数给出系统稳定性判据

博客等级

码龄3年

4
原创

8
点赞

28
收藏

3
粉丝

关注

私信

热门文章

最新评论

单链表数据结构
CSDN-Ada助手: 恭喜您写下了关于单链表数据结构的博客！您对数据结构的理解深入透彻，能够将复杂的概念以清晰易懂的方式呈现给读者。接下来，我建议您可以尝试写一些关于更高级数据结构或者算法的内容，比如双链表、树或者排序算法等。期待看到您更多的精彩作品！ CSDN 正在通过评论红包奖励优秀博客，请看红包流：https://bbs.csdn.net/?type=4&header=0&utm_source=csdn_ai_ada_blog_reply3
ElGamal算法
CSDN-Ada助手: 恭喜你开始撰写博客！ElGamal算法是一个非常有趣和复杂的话题。你的文章对于初学者来说非常友好和易懂。接下来，我建议你可以深入探讨ElGamal算法的数学原理和应用领域，或者提供一些实际的例子来帮助读者更好地理解。期待你的下一篇博客！祝你写作愉快！推荐【每天值得看】：https://bbs.csdn.net/forums/csdnnews?typeId=21804&utm_source=csdn_ai_ada_blog_reply1
古典密码算法
CSDN-Ada助手: 非常棒的博客！你的文章标题和摘要都很吸引人。继续保持创作吧！如果你对古典密码算法感兴趣，还可以深入了解更多有关密码学的知识。例如，你可以了解更多关于对称密码和非对称密码的区别，以及它们在实际应用中的应用。此外，你还可以探索更多的古典密码算法，如凯撒密码、维吉尼亚密码和栅栏密码。这些知识和技能将帮助你更好地理解和应用古典密码算法。再次感谢你的分享！期待你的下一篇博客！如何写出更高质量的博客，请看该博主的分享：https://blog.csdn.net/lmy_520/article/details/128686434?utm_source=csdn_ai_ada_blog_reply2

大家在看

最新文章

目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。