【数据结构】判断二叉树是否是完全二叉树

---

前言

  我们之前在实现链式二叉树的时候，留下了这个 判断二叉树是否是完全二叉树 函数没有实现，而在这篇文章，我们将会非常详细的给大家分析一下这个函数。

一、完全二叉树的概念

  我们知道，二叉树是是由一个根结点加上两颗被称为左子树和右子树的二叉树组成，如下图就是一颗二叉树。

  在了解完全二叉树之前我们需要了解满二叉树。一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。如下图：

  完全二叉树是由满二叉树而引出来的。完全二叉树只有最后一层的结点个数可以没有到达最大值，并且结点都是从左到右前n个，其他所有层的结点数都到达了最大值的就是完全二叉树。

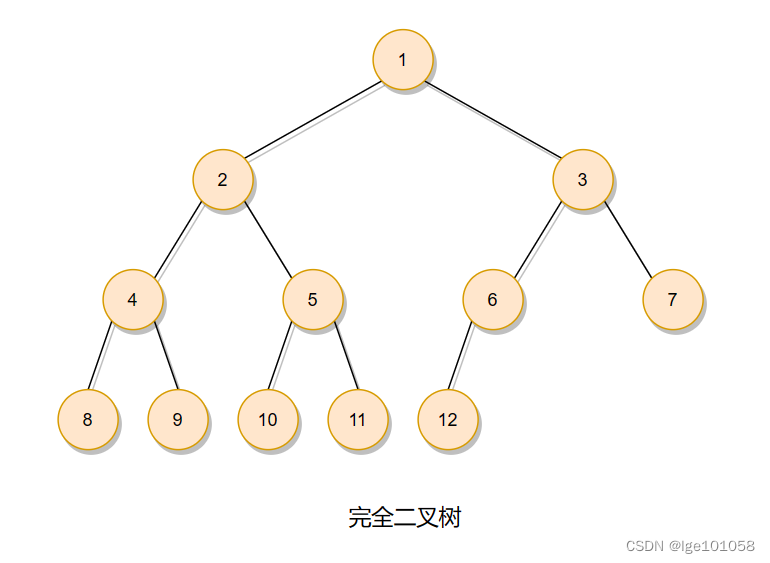
  满二叉树是一种特殊的完全二叉树

二、判断二叉树是否是完全二叉树的思想

  我们发现，完全二叉树的最后一层但肯定是左边先有结点，不可能出现左边出现 NULL 值，右边出现结点，这是非常重要的一个特性。我们可以引申而出，完全二叉树只有最后一层会出现 NULL 值，而且出现了 NULL 值，则后面不会再出现非空的值。我们可以通过层序遍历的思想，一层一层遍历，如果遇到空结点，记录一下，然后继续遍历，若是后面出现了非空值，则说明该二叉树不是完全二叉树。

  那么如何保证遍历是一层一层遍历呢？我们可以借鉴二叉树层序遍历的思想，使用队列结构，每从队头弹出一个结点，就将这个结点的左孩子结点和右孩子结点插入到队列当中，这样就保证了父结点在子结点的前面，左孩子结点在右孩子结点的前面。

三、代码实现

1.库函数头文件及二叉树函数声明

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

// 宏定义二叉树存储的数据类型
typedef char BTDataType;

// 二叉树结构体
typedef struct BinaryTreeNode
{
    // 数据域
	BTDataType data;
	// 指向左孩子的指针域
	struct BinaryTreeNode* left;
	// 指向右孩子的指针域
	struct BinaryTreeNode* right;
}BTNode;

// 通过前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);
// 二叉树销毁
void BinaryTreeDestroy(BTNode* root);

2.队列结构接口

// 队列的数据类型，存的是二叉树结构体指针类型
typedef struct BinaryTreeNode* QDataType;

// 队列的结构体
typedef struct QueueNode
{
	// 队列的数据域
	QDataType val;
	// 队列的指针域
	struct QueueNode* next;
}QNode;

// 传参结构体
typedef struct Queue
{
	// 有一个指向队列的头结点(队头)的指针
	QNode* phead;
	// 有一个指向队列的尾节点(队尾)的指针
	QNode* ptail;
	// 队列的元素个数
	int size;
}Queue;

// 初始化队列
void QueueInit(Queue* pq);
// 销毁队列
void QueueDestroy(Queue* pq);
// 在队尾插入
void QueuePush(Queue* pq, QDataType x);
// 在队头弹出
void QueuePop(Queue* pq);
// 查询队头元素
QDataType QueueFront(Queue* pq);
// 判断队列是否为空
bool QueueEmpty(Queue* pq);

3.其他函数的实现

// 通过前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
    // 如果数组第*pi的值为‘#’，说明遇到了空结点，说明该结点不存在
	if (a[*pi] == '#')
	{
	    // 准备查看数组的下一个元素
		++(*pi);
		// 返回空
		return NULL;
	}

    // 如果当前值不为空
    // 为当前结点开辟一个新的二叉树结构体大小的空间
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	// 开辟空间失败
	if (!root)
	{
	    // 弹出反馈
		perror("malloc fail");
		// 退出程序
		exit(-1);
	}

    // 开辟空间成功
    // 将当前的数组的值赋值给该结点的数据域，并让*pi增加1，准备查看下一个数组元素
	root->data = a[(*pi)++];
	// 递归传回该结点的左孩子的地址
	root->left = BinaryTreeCreate(a, pi);
	// 递归传回该结点的右孩子的地址
	root->right = BinaryTreeCreate(a, pi);
	// 返回当前结点的地址
	return root;

// 二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{
    // 空结点直接返回
	if (!root)
		return;
	
	// 递归左孩子
	BinaryTreeDestroy(root->left);
	// 递归右孩子
	BinaryTreeDestroy(root->right);
	// 销毁根结点
	free(root);
}


// 队列接口函数
// 队列初始化
// 传入传参结构体成员的地址
void QueueInit(Queue* pq)
{
	// pq是指向传参结构体的指针，只要结构体创建了，那pq就不可能为空，为空说明传参错误或者结构体没创建
	assert(pq);
	
	// 让指向首元结点的头指针和指向尾结点的尾指针置空，说明队列为空
	pq->phead = pq->ptail = NULL;
	// 队列目前有效数据为0
	pq->size = 0;
}

// 销毁队列
void QueueDestroy(Queue* pq)
{
    // pq不可能为空，可以断言一下以免出现小差错
	assert(pq);

    // 如果pq指向的结构体里面的phead不为空，即存在结点
	while (pq->phead)
	{
	    // 创建一个临时指针变量指向首元结点
		QNode* tmp = pq->phead;
		// 让phead指向第二个结点
		pq->phead = pq->phead->next;
		// 释放首元结点空间
		free(tmp);
		// 释放空间后指针置空是好习惯
		tmp = NULL;
	}
	// 最后没有结点的时候，把尾结点置空
	pq->ptail = NULL;
	// 让有效数据大小为0
	pq->size = 0;
}

// 入队列
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);

	// 为新结点开辟空间
	QNode* newNode = (QNode*)malloc(sizeof(QNode));
	// 开辟失败时
	if (newNode == NULL)
	{
	    // 弹出反馈
		perror("malloc fail");
		// 终止程序
		exit(-1);
	}
	// 为新结点赋值
	newNode->val = x;
	newNode->next = NULL;

	// 当队列为空时
	if (pq->ptail == NULL)
	{
	    // 头指针指向新结点
		pq->phead = pq->ptail = newNode;
	}
	// 当队列非空时
	else
	{
	    // 原尾结点的指针域指向新结点
		pq->ptail->next = newNode;
		// 尾指针指向新结点
		pq->ptail = newNode;
	}
	// 队列的有效个数+1
	++pq->size;
}

// 出队列
void QueuePop(Queue* pq)
{
	assert(pq);
	// 队列为空不能删除
	assert(pq->phead);

    // 临时指针指向首元结点
	QNode* tmp = pq->phead;
	// 当队列中只有一个结点时
	if (pq->phead == pq->ptail)
	{
	    // 将两个指针置空
		pq->phead = pq->ptail = NULL;
	}
	// 当队列中不止一个结点时
	else
	{
	    // 让头结点指向第二个结点
		pq->phead = pq->phead->next;
	}
	// 有效数据个数-1
	--pq->size;
	// 释放原首元结点的空间
	free(tmp);
	// 释放空间后指针置空
	tmp = NULL;
}

// 查询队头数据
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	// 队列不为空才有队头数据
	assert(pq->phead);
    
    // 根据头指针找到队头数据
	return pq->phead->val;
}

// 判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);

    // 返回队列有效数据的个数是否等于0来判断队列是否为空
	return pq->size == 0;
}

4.判断二叉树是否是完全二叉树函数

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	// 创建一个队列
	Queue q;
	// 初始化队列
	QueueInit(&q);
	// 如果根结点存在
	if (root)
		// 根结点入队列
		QueuePush(&q, root);
	// 队列非空
	while (!QueueEmpty(&q))
	{
		// 记录队头元素
		BTNode* front = QueueFront(&q);
		// 将队头元素出队列
		QueuePop(&q);

		// 如果队头元素为空
		if (!front)
			// 跳出while循环
			break;

		// 左孩子入队列
		QueuePush(&q, front->left);
		// 右孩子入队列
		QueuePush(&q, front->right);
	}

	// 遇到空且队列尚未结束
	while (!QueueEmpty(&q))
	{
		// 记录队头元素
		BTNode* front = QueueFront(&q);
		// 弹出队头元素
		QueuePop(&q);
		// 遇到了非空元素
		if (front)
		{
			// 销毁队列
			QueueDestroy(&q);
			// 不是完全二叉树
			return false;
		}
	}

	// 队列空了
	// 销毁队列
	QueueDestroy(&q);
	// 是完全二叉树
	return true;
}

  前面已经说过，判断二叉树是否是完全二叉树的精华就在层序遍历的条件下查找是否存在空结点在非空结点的前面，如果存在则说明该二叉树不是完全二叉树，如果不存在，空结点后面只有空结点，则说明该二叉树是完全二叉树。

5.主函数

int main()
{
    // 创建二叉树数据，‘#’代表空结点
	char a[] = "ABD##E#H##CF##G##";
	int b = 0;
	// 通过前序遍历构建二叉树二叉树
	BTNode* root = BinaryTreeCreate(a, &b);
	printf("是否是完全二叉树：");
	if (BinaryTreeComplete(root))
	    // 是
		printf("true\n");
	else
	    // 不是
		printf("false\n");
	// 销毁二叉树
	BinaryTreeDestroy(root);
	// 销毁空间后指针置空
	root = NULL;
	return 0;
}

6.结果演示

  我们创建的数据为 “ABD##E#H##CF##G##” ，这个前序遍历的结果，所以我们将这个二叉树画出来。

  显而易见，这不是完全二叉树。让我们来看看结果：

  当然，读者也可以自己更改数据，创建一个完全二叉树来验证结果。

---

总结

  本篇文章到这里就结束了，希望对你有所帮助，谢谢。如果在文中发现错误，还请不吝赐教。