1.监督学习（上）_成本函数在房价预测中的作业-CSDN博客

本文链接：https://blog.csdn.net/m0_70078527/article/details/144618743

一.线性回归（Linear Regression Model）：

输出无限多可能的数字。

【示例1】房价预测：

【图一】

假设您想根据房屋的大小预测房屋的价格，横轴：以平方英尺为单位的房屋大小，纵轴：是以千美元为单位的房屋价格。这里的小十字字中的每一个都是一所房子，其大小和价格是最近出售的。假设你是房地产经理，客户问你某个房子的价格可以出售多少钱，该数据集可能会帮助你估算一个大概价格，测量房子的大小，结果房子是1250平方英尺，这样，你可以在该数据集构建一个线性回归模型，这个模型将数据拟合一条直线，它可能看起来如蓝色的线一般；从而根据这条与数据拟合的直线，可以看到房子1250平方英尺处与最佳拟合线相交，沿着左边的垂直轴追踪得到价格也许在220,000美元。
称之为监督学习，因为首先通过提供具有正确答案的数据来训练模型。因为先获得房屋模型示例（大小以及模型）应为每栋房屋预测的价格。也就是说为数据集中的每个房子都给出了正确答案。
这种线性回归模型是一种特殊类型的监督学习模型，称为线性回归，因为预测数字作为输出，如美元价格；任何预测如220,000或1.5或负数33.2之类的数字的监督学习模型都在解决所谓的回问题
数据可视化图可以是左侧也可以是右侧。右侧的数据表中假如有47行，那么在左图上就有47个十字，每一个X对应表格的一行。

1.概念：

训练集：用于训练模型的数据集；
- 比如：上图的数据价格和尺寸，请注意，客户的房子不在此数据集中，因为它尚未售出，所以没有人知道价格是多少，要预测客户的房价，首先训练模型以从训练集中学习，然后该模型可以预测客户的房价。
输入变量（或特征）：房屋尺寸表示输入的标准符号是小写的x；
- 例：对于训练集中的第一个房子，x是房子的大小，因此x=2104；
输出变量（目标变量）：尝试预测的输出变量的标准符号是小写的y；
- 例：输出的y=400，也就是房子价格

数据集中每栋房子一行，在这个训练集中，有47行，每一行代表一个不同的训练示例。m=47表示训练示例总数，（x，y)表示单个训练示例.引用一个具体的训练例子，这会对应【图一】中的右图，

例：（x^(1),y^(1)）=（2104,400）指第一个训练模型；

2.工作原理：

监督学习训练集包括输入特征（例如房屋大小）和输出目标（例如房屋价格），输出目标是我们将从中学习的模型的正确答案，要训练模型，需要训练集（包括输入特征和输出目标）提供给的学习算法，然后监督学习算法就会产生一些功能，我们将这个函数写出小写的f：代表函数；历史上，这个函数曾经被称为假设。
f的工作是采用新的输入x和输出并进行估计和预测，将其称为y-hat，它的写法类似于顶部带有这个小帽子符号的变量；机器学习中是估计或预测的，f为模型，x为输入/输入特征，模型的输出是预测。所以模型的预测是y的估计值。
模型f在给定大小的情况下，输出作为估算器的价格，即对真实价格的预测。

【注意】只有字母y时，指目标，即训练集中的实际真实值，相反或y-hat是一个估计值，可能不是一个实际的真实值

2.1.公式：

设计算法时，如何表示函数f/计算f的数学公式是什么？
- 现在让我们坚持f是一条直线，函数可以写成，但现在，只知道w和b是数字，为w和b选择的值将根据输入特征x确定预测y-hat，所以f、w、b、x意味着f是一个以x作为输入的函数，并且根据w和b的值，f将输出预测y-hat的某个值；作为该式子中f（x）而没有明确的将w和b包含在下标中，让我们在图表中绘制训练集，其中输入特征x在水平轴上，输出目标y在垂直轴上；请记住，该算法从这些数据中学习并生成最适合的线，下图在的函数作用使用x的流程函数预测y的值。
为什么我们会选择线性函数，其中线性函数知识直线的术语，而不是非线性函数，如曲线或抛物线？
- 拟合更复杂的非线性函数，下图黑色的线，但是由于此线性函数相对简单易于使用，让我们使用一条线作为基础，最终将帮助获得更复杂的非线性模型。
线性回归：是具有一个变量，表示只有一个输入变量或特征x，也可称为单变量（Univariate）线性回归。如：房屋大小；
- 单变量只是说一个变量的一种奇特方式。

3.成本函数/代价函数：

3.1.重要性：

构建一个成本函数，该思想是机器学习中最普遍和最重要的思想之一，用于线性回归和训练世界上许多先进的人工智能模型。

3.2.概念：

为了实现线性回归，第一个关键步骤就是首先定义一个成本函数，成本函数将告诉我们模型的运行情况，以便我们可以尝试让它做的更好。

例：有一个包含输入特征x和输出目标y的训练集，需要拟合这个训练集的模型是这个线性函数。机器学习中，模型的参数是可以在训练期间调整以改进模型的变量。
w和b：模型的参数（parameters）或系数或权重。根据w和b选择的值，会得到x的不同函数f，会在图形上生成不同的线：
- 解析：
  - w=0,b=1.5时，f如最左图所示，这种情况下，x的函数f是0乘以x+1.5，因此f始终是一个常数值；它总是预测y的估计值=1.5；所以y-hat始终等于b，b也称为y的截距，因为这是它与垂直轴或此图上y轴相交的地方；
  - w=0.5，b=0，则图如中间图所示，斜率为0.5，w的值给出了直线的斜率即0.5；
  - w=0.5，b=1，如最右图显示，w斜率为0.5；
假如，有一个像【图二】所示的训练集，对于线性回归，要做的是选择参数w和b的值，以便从函数f获得的直线以某种方式很好的拟合数据。就像蓝色的线一样，当看到这条线在视觉上与数据相符时，你可以认为这意味着f定义的线大致穿过或接近训练示例的某个地方，而其它可能的线则不太接近这些点。
只是为了提醒您，像这里的训练示例由x上标i，y上标i定义，y是目标。对于给定的输入 x^i ,函数f也为 y^i 做出预测值，并且它对y的预测值是 ^i ,对于我们选择的x^i的模型f是w*x^i+b；换句话说，预测t^i是f、wb、x^i；其中对于我们使用的模型，f、x^i等于wx^i+b。现在的问题是如何找到w和b的值，以便对于许多或可能所有训练示例x^i、y^i的预测^i接近真实目标y^i.
要回答这个问题，我们先来看看如何衡量一条直线与训练数据的拟合程度，为此，构建成本函数：采用预测并通过取减去y将其与目标y进行比较，这种差异称为误差。我们正在测量预测与目标的距离，我们计算这个误差的平方。此外，我们将为训练集中不同的训练示例i计算此项。当测量误差时，例如i，我们将计算这个平方误差项，最后我们要测量整个训练集的误差。特别是让我们像下图这样总结平方误差（将i=1,2，3……一直加到m，并记住m是训练示例的数量），对于这个训练集来说是47。
按照惯例，为了构建一个不会随着训练集大小变大而自动变大的成本函数，我们将计算平方误差而不是总平方误差，我们通过像这样除以m来实现。按照惯例，机器学习使用的成本函数实际上是除以1/2m，额外除以2只是为让我们后面的一些计算看起来更整洁；但无论是否包含除以2，成本函数仍然有效。此外，表达式是成本函数，我们将写J（w，b）来指代成本函数，这也称为平方误差成本函数，之所以这样称呼是因为取到这些误差项的平方。
在机器学习中，不同的人会针对不同的应用程序使用不同的成本函数，但平方误差成本函数是迄今为止线性回归最常用的函数。就此而言，对于所有回归问题，它似乎为许多应用程序提供了良好结果。提醒一下，=模型f在x处的输出，我们可以将J(w,b)重写为1/2m∑（f(x^(i)-y^(i))）^2。最终我们将要找到使成本函数变小的w和b的值。但在这之前，我们首先更直观的了解J（w,b）真正在计算什么。

【注意】如果我们有更多的训练示例，m会更大，您的成本函数将计算出更大的数字，这是更多示例的总结。

【图二】

3.3.直观理解：

（1）如何使用成本函数为模型找到最佳参数？

你想对训练数据拟合一条直线，所以有【如图所示】模型模型的参数：w和b。现在根据这些参数选择的值，就会得到这样的不同直线。如果你想要找到w和b的值，以便直线很好的拟合训练数据，为了衡量w和b的选择与训练数据的拟合程度，你有一个成本函数J，它衡量模型预测与y的实际真实值之间的差异。所以，线性回归会尝试找到w和b的值，然后使J尽可能小。在数学中，我们这样写：，我们想要最小化J作为w和b的函数。现在，为了让我们更好的可视化成本函数J，我们使用线性回归模型的简化版本：使用，可以认为这是取左边的原始模型，去掉参数b或b=0；它只是偏离了等式，所以f现在只是w*x。所以，现在只有一个参数w，成本函数J看起来与之前相似，取差求其平方，也就是wx^(i),而J现在只是w的函数。目标也变得有点不同，因为只有一个参数w，所以使用这个简化的模型。目标是找到w的值，使w的J最小化。从视觉上看，这意味着如果b=0，则f定义一条看起来像【右图所示】的线，可以看到直线经过原点，因为当x=0，=0。

（2）现在使用这个（）简化模型，让我们看看当参数w选择不同的值时成本函数如何变化？

看一下的模型和成本函数J（w）的图表。
- 绘制【如图所示】理解两者间关系：首先注意到，对于f下标w，当参数w固定不变时（即始终为常数时），则只是x的函数，也就是说y的估计值取决于输入x的值。
- 相反，【右图】中成本函数J是w的函数，其中w控制由定义的直线斜率。J定义的成本取决去参数，在本例中为参数w。
从模型中开始，【左侧】x函数，这里输入特征x的水平轴上，输出值y在垂直轴上。这里十字代表训练集位置（1,1），（2,2），（3,3）的三个点的图。让我们为w选择一个值。
- 假设w=1，，函数斜率为1的直线。接下来做计算w=1的成本J（w），对于这个w值，事实证明成本函数中的误差项，这个（w*x^i减去y^i）对于数据点的每一个都等于0。因为对于这个数据集，当x=1是，y=1，当w=1时，则f(x)=1。因此，对于一个训练示例，f(x)=y，差值=0，将其代入成本函数J，得到0的平方；同样，x=2,y=2,f(x)=2,在成本函数中，第二个示例的平方误差=0的平方；最后x=3,y=3,f(x)=3，在成本函数中，第三个示例的平方误差=0的平方。对于这个训练集中所有三个示例，对于每个训练示例i，f(x^i)=y^i,因此f(x^i-y^i)=0。
对于特定的数据集，当w=1，成本J=0，现在，在【右侧】绘制成本函数J。请注意，因为成本函数是参数w的函数，所以水平轴现在标记为w而不是x，垂直轴现在标记为J而不是y。J（w）=0（w=1时）。现在，让我们看一下f和J如何随着w的不同值而变化，w可以取一个范围的值，所以w可以取负值，w可以是0，也可以去正值。

（3）如果w=0.5，那么这些图是怎么样的？

w=0.5，在这种情况下，函数f(x)现在看起来像【左图】所示，是一条斜率为0.5的直线，成本J【如右图】，成本函数测量的是估计值之间的平方误差或差异，即，即和真实值，即每个示例,从视觉上可以看出，x=1时，误差或差异等于此处垂直线高度（十字到w=0.5的线的距离），因为下面这条线是y的实际值和函数f预测的值之间的差距，这里更靠下一点。
- 对于第一个示例，当x=1时，f(x)=0.5，第一个示例的平方误差为（0.5-1）^2=0.25，记住成本函数，我们将对训练集中所有训练示例求和；第二个示例，x=2，f(x)=1，y实际值为2，平方误差（1-2）^2=1【也就是十字到斜线的距离】；第三个例子，重复此过程，此处的误差（也由此线段）为（1.5-3）^2=2.25,。接下来，将0.25+1+2.25=3.5，3.5*（1/2m）=0.58，其中m是训练示例数量，所以成本J=0.58，绘制【右图】。

（4）w=0：

w=0,那么x的f就是这条正好在x轴上的水平线【黄色的线】，每个示例的误差是一条线，从每个点向下延伸到代表x的f=0的水平线。成本J=1/（2m）*（1^2+2^2+3^2）=2.33，在【右图】绘制w=0，J=2.33的点。
由此w可以是任何数字，它可以是负值，如果w=-0.5，那么f线就是【浅蓝色】【左图】这样一条向下倾斜的线，事实证明，当w=-0.5时，成本会更高，约为5.25。您可以继续计算不同w值的成本函数，以此类推并绘制它们。
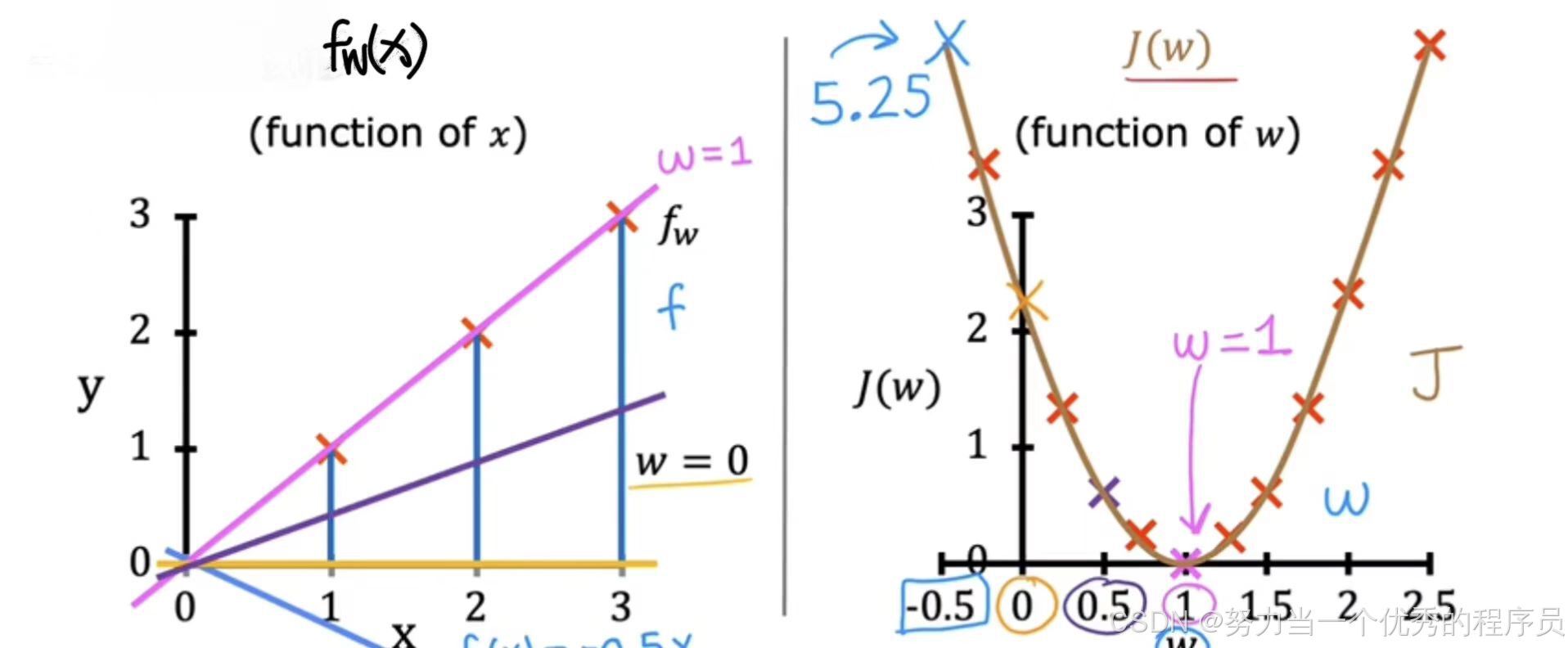事实证明，通过计算一系列的值，您可以慢慢找出成本函数J的样子，就是J是什么【如右图】曲线。回想一下，参数w的每个值对应于左图上不同的直线拟合，对于给定训练集，对于w值的选择对应于【右侧图表上】的单个点，因为对于w的每个值，可以计算w的成本J。如，当w=1时，对应于通过数据拟合的这条直线，也对应于J图上的这一点，其中w=1【粉色】的线,J=0。而当w=0.5时，【紫色】这条线的斜率较小。这条线与训练集相结合，对应于成本函数图上w=0.5时这一点，对于w的每个值，最终会得到一条不同的线及其相应的成本J（w），您可以使用这些点绘制出【右侧】的这张图。

（5）鉴于此，您如何选择产生函数f的w值，从而很好的拟合数据？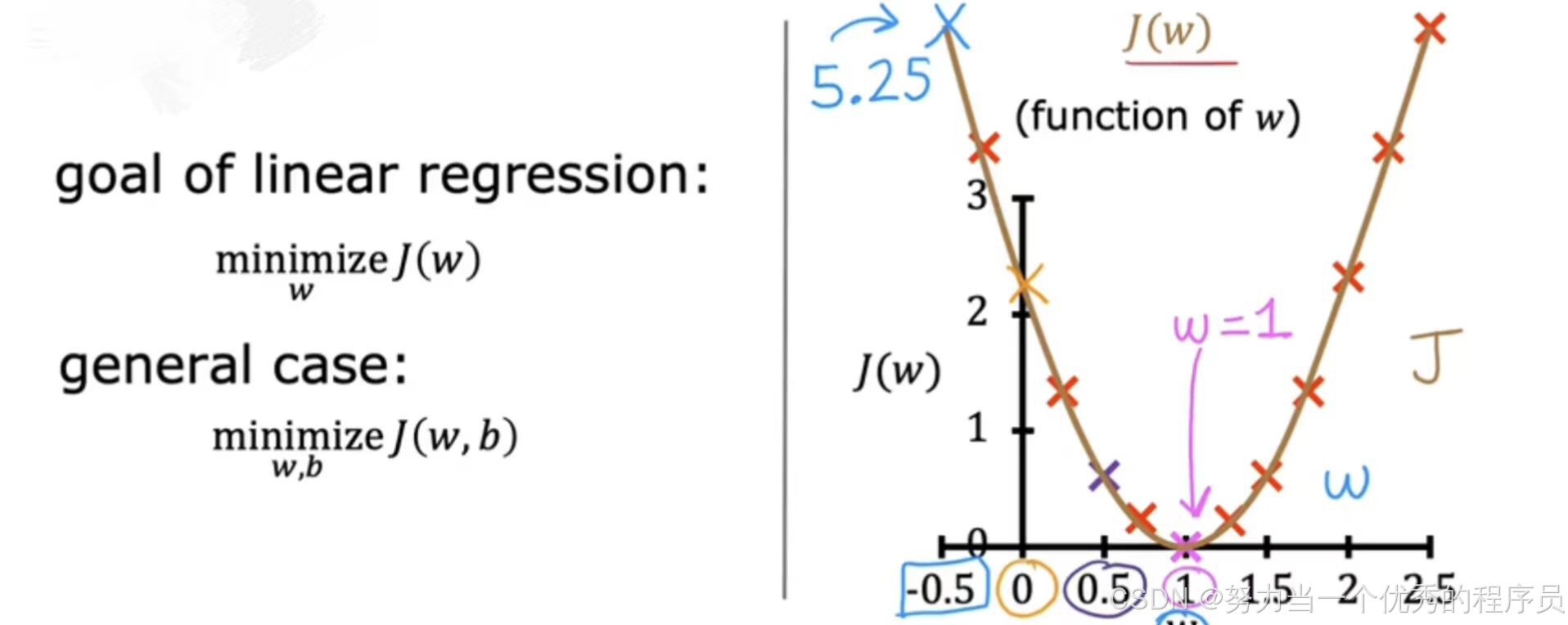

正如可以想象的那样，选择一个J（w）尽可能小的w值似乎是一个不错的选择，J是衡量平方误差有多大的成本函数，因此选择最小化这些平方误差w，使它们尽可能小，将为我们提供一个好的模型。在此示例中，如果您选择的w值会导致J（w）的最小可能值，您最终会选择w=1。如您所见，这实际上是一个不错的选择，这导致直线非常适合训练数据，这就是在线性回归中如何使用成本函数来找到使J最小化的w值。在更一般的情况下，我们有参数w和b而不仅仅是w，您会找到使J最小化的w和b的值。

（6）总结：

当改变w或改变w和b时，您最终会得到不同的直线，当该直线穿过数据时，导致J很小。线性回归的目标是找到参数w或w和b，使成本函数J的值最小。

4.可视化：

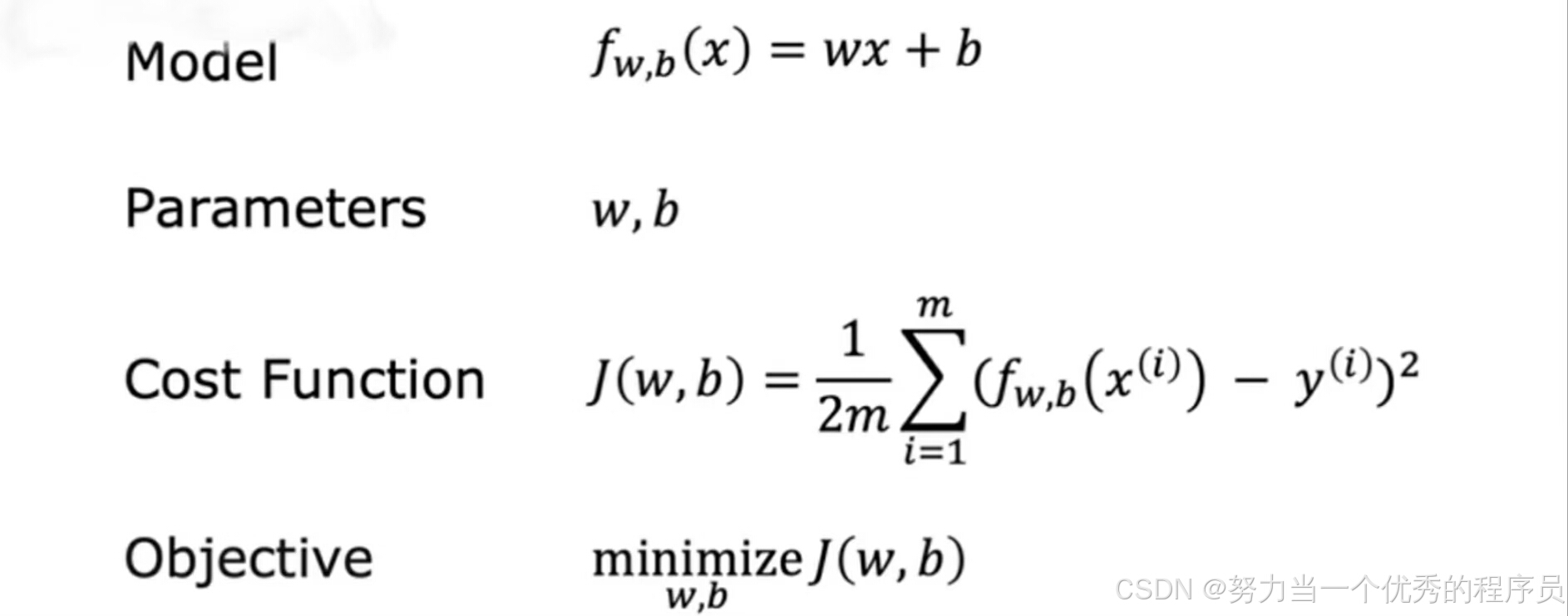
目前为止，我们所看到的模型、模型参数、成本函数以及线性回归的目标【如图所示】，3.3中我们暂时将b设置为0以简化可视化，现在，我们带回参数w和b的原始模型，但不将b设置为0。
我们想要更直观的了解模型函数，【如下图所示】这是一组房屋大小和价格的训练集，假设选择了x的一个可能函数，在这里，w=0.06，b=50。请注意，对于这个训练集来说，这不是一个特别好的模型，实际上是一个非常糟糕的模型，一直在低估房价。

（1）给定w和b的这些值，成本函数可能是什么样？

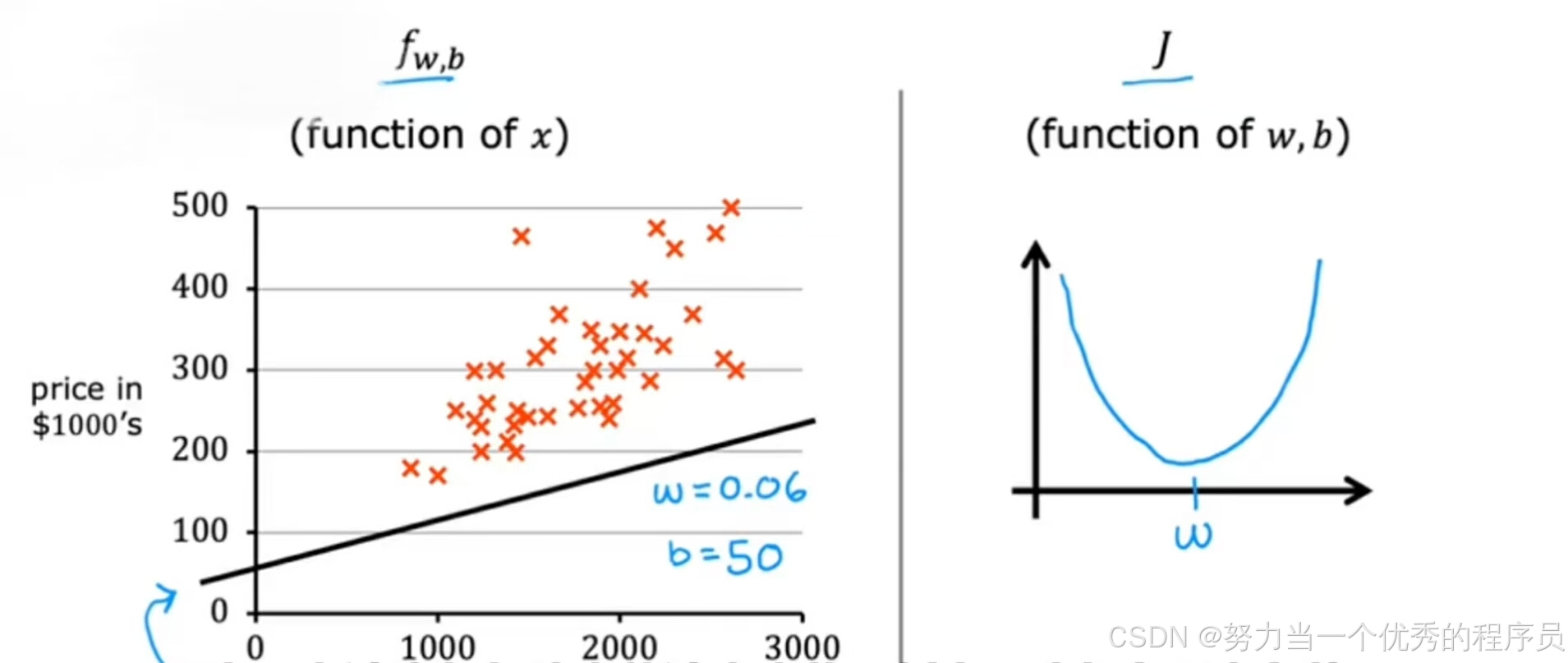
3.3中的只有w的情况下，我们暂时b=0简化事情，后来得出一个成本函数，看起来像仅为w的函数。当我们只有一个w参数时，成本函数呈现U型曲线，形状有点像汤碗。
【如图所示】，现在左图的房价预测中，我们有两个参数w和b，事实证明，成本函数应具有类似汤碗的形状，只是在一个三维度而不是两个维度。事实上，根据训练集，成本函数看起来像：，这里的3D曲面图，其中轴标记为w和b。当改变模型的两个参数w和b时，您会得到w和b的成本函数J的不同值。这个表面上的任何一个点都代表w和b的某种特定选择。
现在，为了更仔细观察特定点，还有另一种绘制成本函数J的方法，这对可视化非常有用。也就是说，我不使用这些 3D表面图，而是采用完全相同的函数J，我根本没有改变函数J并使用称为等高线图的东西绘制。

4.1.等值线图/等高线图：

【如图所示】它实际上是一个非常延伸的碗，，在可选实验室中，您将能够以3D形式看到它并不是自己绕着表面旋转，在那里看起来更明显的呈现碗状，【右上角】是与底部完全相同的成本函数的等值线图，此等值线图上两个轴是b，在垂直轴上，w是在水平轴上。这些椭圆形中每一个显示3D表面上处于完全相同高度的中心点。换句话说，对于成本函数J具有相同值的点集，要获得等值线图，请在底部取3D表面，然后用刀将其水平切片，并获得所有点，它们处于同一高度，因此，每个水平切片最终显示这椭圆之一。具体来说，如果你取了三个点，成本函数J都具有相同的值，即使它们的w和b值不同。在【左上图】中，可以看到这三个点对应于不同的函数f，在这种情况下，这三个点对于预测房价实际上都非常糟糕。现在，成本函数J最小的碗底就是【右上角】这个同心椭圆的中心点。事实证明，等值线图是可视化3D成本函数J的一种便捷方式，但在某种程度上，它只是以2D形式绘制。

4.2.参数影响：

（1）参数不同选择如何影响f(x)以及成本J的不同值？

【例1】

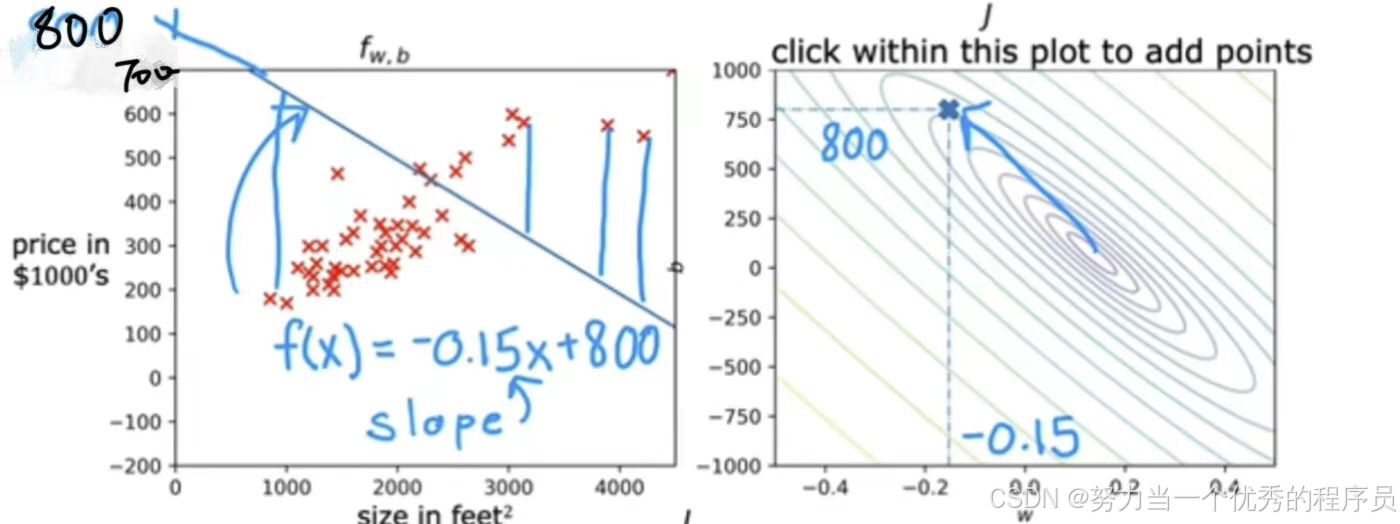
在【如图】J上有一个特定点，对于这一点，w≈ -0.15，b≈ 800，该点对应于使用特定成本J的一对w和b的值。事实上，这对于w和b的值对应于f(x)，也就是【左图】的这一条线，在800处与垂直轴相交，因为b=800，并且线的斜率w=-0.15。现在查看训练集中数据点，会注意到这条线不太适合数据，对于f(x)=-0.15x+800，使用w和b这些值，y值许多预测与训练数据中y的的实际目标值相差太远。因为这条线不太适合，如果查看J的图表，这条线的成本就在【右图】蓝色箭头处，与最小值相差太远，成本相等高，因为w和b这种选择不太适合训练集。

【例2】

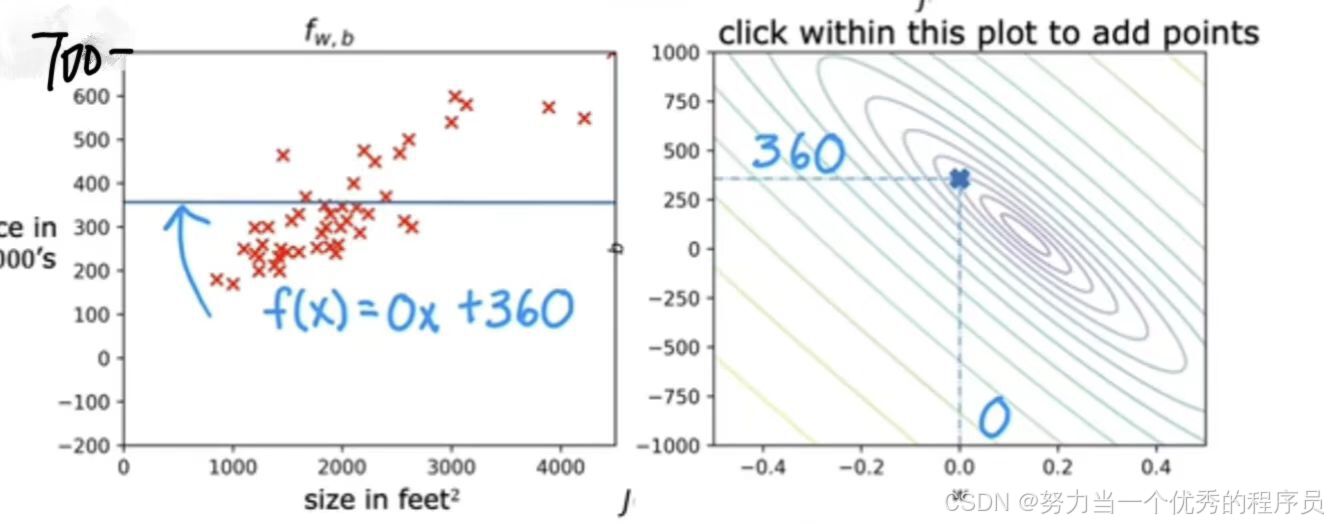
这里另一个函数仍然不太适合数据，但可能稍微好一点。这里的这一点代表该行的w和b的成本，w=0，b≈360。这对参数对应这个函数是一条平线，因为f(x)=360。

【例3】

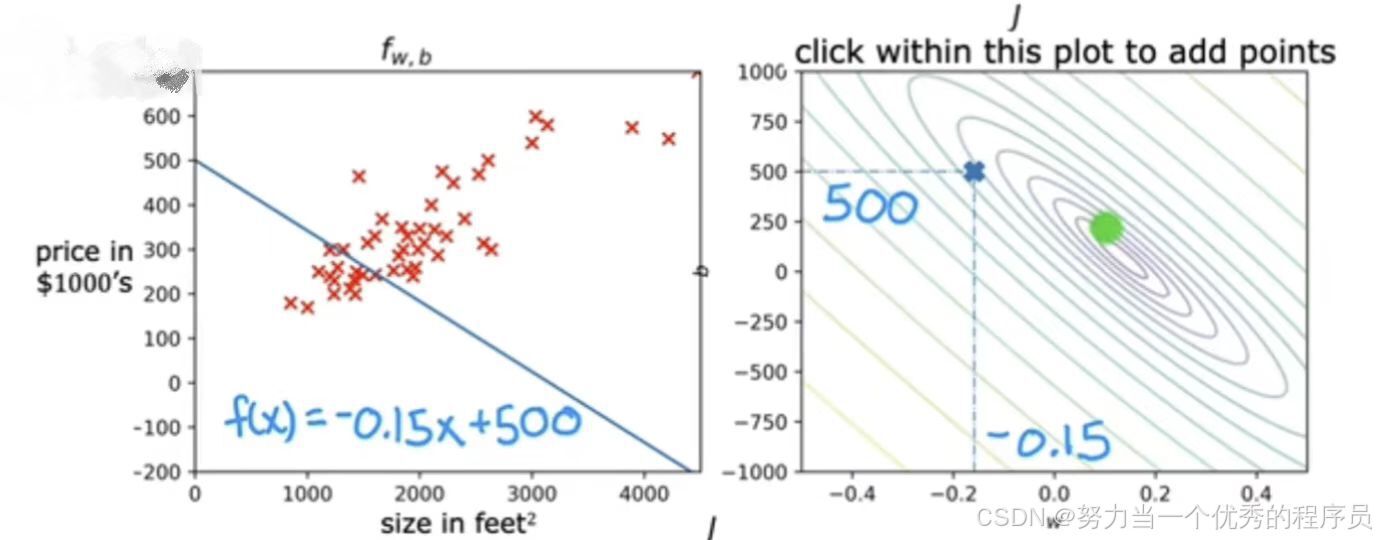
w≈-0.15，b≈500，f（x）=-0.15x+500。同样，与数据不太吻合，实际上与前面的实力相比离最小值更远。

【例4】

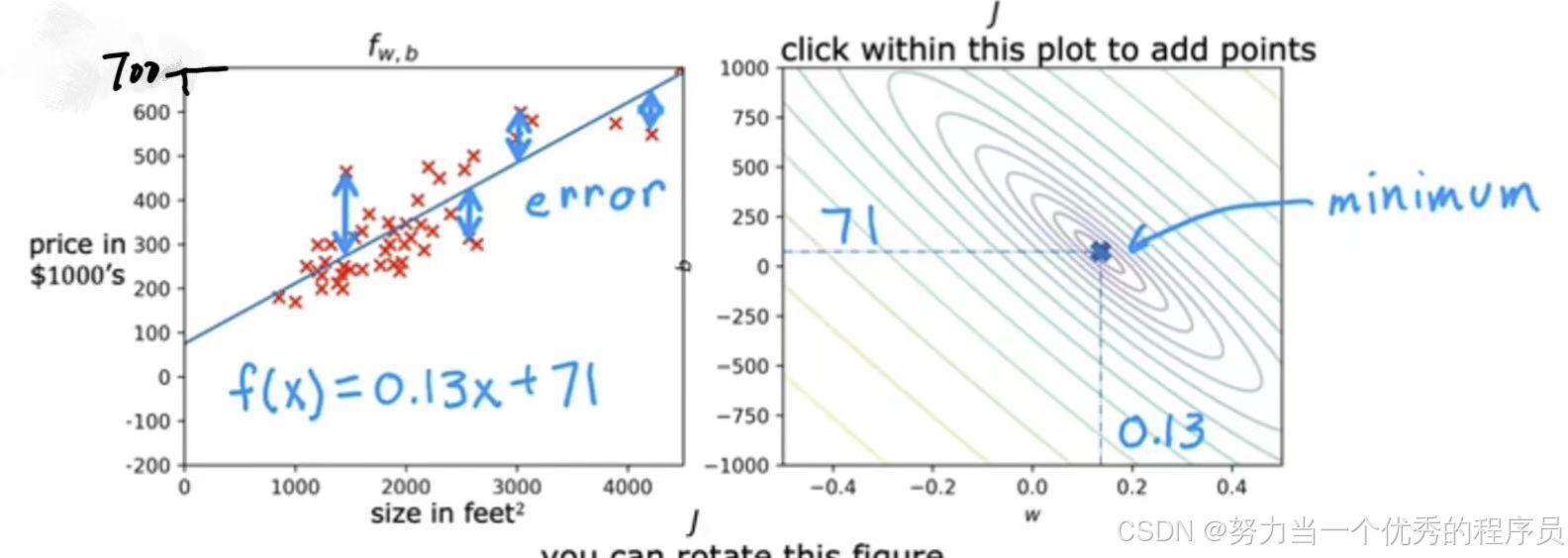
w≈0.13，b≈71，f（x）=0.13x+71。【左图】f（x）看起来非常适合训练集，在【右图】看到，代表成本这个点非常接近较小椭圆的中心，他不是完全最小值，但已经非常接近了。如果测量直线上数据点与预测值之间垂直距离，则会得到每个数据点的误差，所以这些数据点的误差平方和非常接近所有可能的直线拟合中的最小误差平方和。

这四个例子说明了更好的拟合线对应于J图上更接近w和b的成本函数J的最小可能成本的点。

【注意】这四个例子最小值位于最小椭圆的中心。

二.梯度下降：

1.介绍：

1.1.概念：

机器学习中最重要算法之一，梯度下降和梯度下降的变体不仅用于训练线性回归，还用于训练所有AI中一些最大和最复杂的模型。

作用：更系统的方法找w和b的值，缩小J的可能成本。
使用范围：机器学习中线性回归，还可以训练一些最先进的神经网络模型，也称为深度学习模型。

1.2.如何使用：

有w和b的成本函数J，想最小化它。在我们目前看到的示例中，这是线性回归的成本函数。但事实证明，梯度下降是一种可用于尝试最小化任何函数的算法，而不仅仅是线性回归的成本函数。只是为了让关于梯度下降的讨论更普遍，事实证明，梯度下降适用于更一般的函数，包括用于具有两个以上参数的模型的其他成本函数。例如：如果有一个成本函数，目标是参数和b上最小化J。换句话说，想要和b的选择值，从而为您提供J的最小可能值。事实证明，梯度下降是一种算法，也可以应用它来尝试最小化此成本函数J。
只需要对w和b的一些初始猜测开始，在线性回归中，初始值是多少并不重要，所以一个常见的选择是它们设置为0。例如，w=0，b=0作为初始猜测，使用梯度下降算法，要做的是，你每次都稍微改变参数w和b以尝试降低w和b的成本J，直到希望J稳定在或接近最小值。应该注意，对于某些不可能是弓形或吊床形的函数J，可能不止存在一个最小值。【如图所示】更复杂的曲面图，对于具有平方误差成本函数的线性回归，总是以弓形或吊床形结束。【此图】不是平方误差成本函数，但这是训练神经网络模型时可能会得到的一种成本函数，注意轴，即底部轴上的w和b，对于不同w和b的值，你会在这个表面上得到不同的点，J（w,b）其中表面在某个点的高度就是成本函数的值。

（1）现在，我们想象一下，这个表面实际上是一个略带丘陵的户外公园或高尔夫球场的视图，其中高点是山丘，低点是山谷。假如你站在山顶，想要尽可能高效的到达这些山谷之一的底部，梯度下降算法要做的是，你在山顶旋转360度并环绕四周问自己如果我要朝一个方向迈一小步，我想要尽快下坡到或一个这些山谷，我选择朝哪个方向迈出一小步？

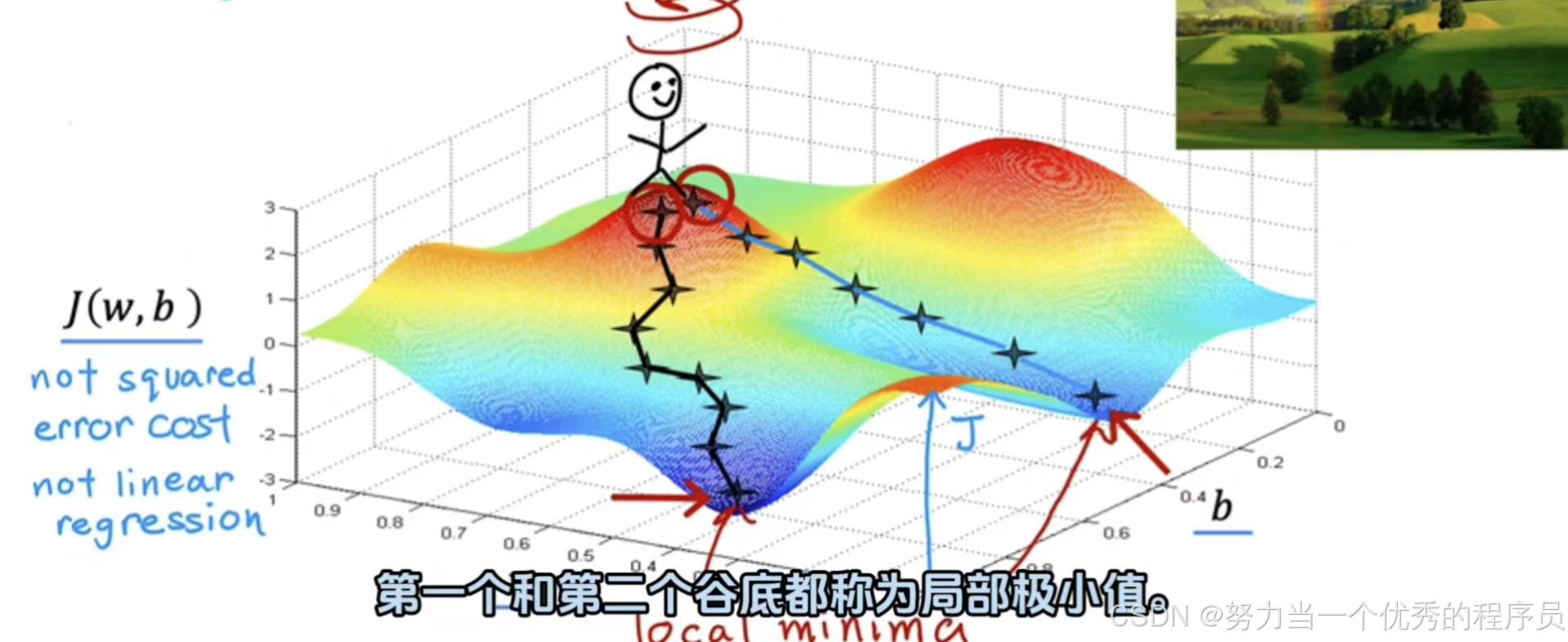
如果想要尽可能高效的走下这座删，事实证明，如果站在山上这个点环顾四周，会发现下山最佳方向是箭头所指，从数学上讲，这是最快速下降的方向。这意味着当你迈出一小步时，这比你在任何其他方向上迈出一小步都要快。迈出第一步后，在所在位置重复这个过程，站在新点上，再次旋转360度，朝哪个方向迈出一小步？如此往复该步骤，刚才经历的这些就是梯度下降的多个步骤，事实证明，梯度下降是有一个有趣的特性：请记住，你可以通过参数w和b选择起始值来选择表面的起始点。
假设起点变了，使用梯度下降，将会进入另一个山谷，最右边的那个，第一个和第二个谷底都称为局部极小值。如果开始沿着第一个山谷走下去，梯度下降不会把你带到第二个山谷是，同样第二个不会把你带到第一个。

1.3.如何实现：

（1）实现步骤：

步骤一：每一步中，参数w更新为。
- 这个表达式意思是，在参数w之后，取w的当前值并对其少量调整。也就是右边的这个表达式。【注意】：这里的=是赋值运算符。
  - α：学习率：控制更新模型参数w和表示采取的步骤大小。通常是0~1之间的一个小正数，可以说是0.01。α它基本控制你下坡的步幅，如果α非常大，那么这对应于一个非常激进的梯度下降过程，你正在尝试采取巨大步骤下坡；反之，α非常小，那么你下坡时会像小婴儿一样步履蹒跚。
  - 成本函数J的导数项，结合α，决定了你想要下坡的步数大小。该导数来自微积分。
步骤二：该模型有两个参数w和b，还有一个赋值操作更新看起来非常相似的参数b，。
请记住，在曲面图的图形上，可以采取一些小步骤，直到到达底部，对于梯度下降算法，将重复这两个更新步骤，知道算法收敛。通过收敛，达到局部最小值，其中w和b不再随着采取的每个额外步骤而发生太大变化。现在，关于如何正确进行语义梯度下降还有一个更微妙的细节，你将更新两个参数w和b。一个重要的细节对于梯度下降，同时更新w和b意味着在表达式中，将w从旧的w更新为新的w，并且b也得更新为新的b。实现方法是计算右侧，计算w和b这个东西，同时更新w和b的新值。，，计算手边的两个更新，并将它们存储到变量temp_w和temp_b中，然后将这两个值赋值到w和b中。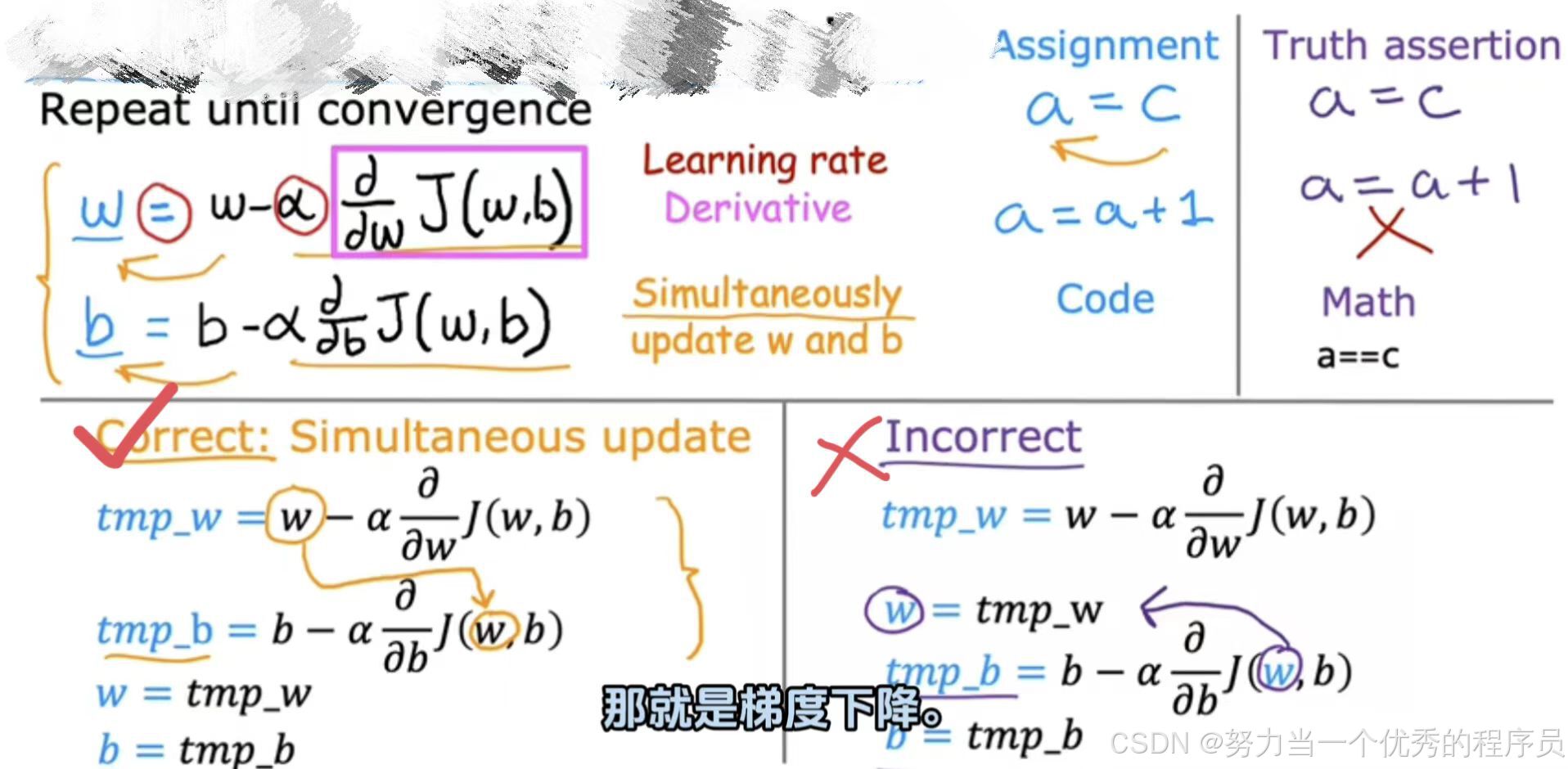

【如图所示】下方右侧和左侧实现之间区别在于，如果w已经更新为心智，并且这个更新的w实际上进入导数项的的成本函数J（w,b）。这意味着这个术语与您在左侧看到的术语是不同的，梯度下降的代码中实现方式，实际上证明以正确的方式实现同步更新更为自然。

2.梯度下降直观理解：

<1>让我们使用一个稍微简单的例子，致力于最小化一个参数。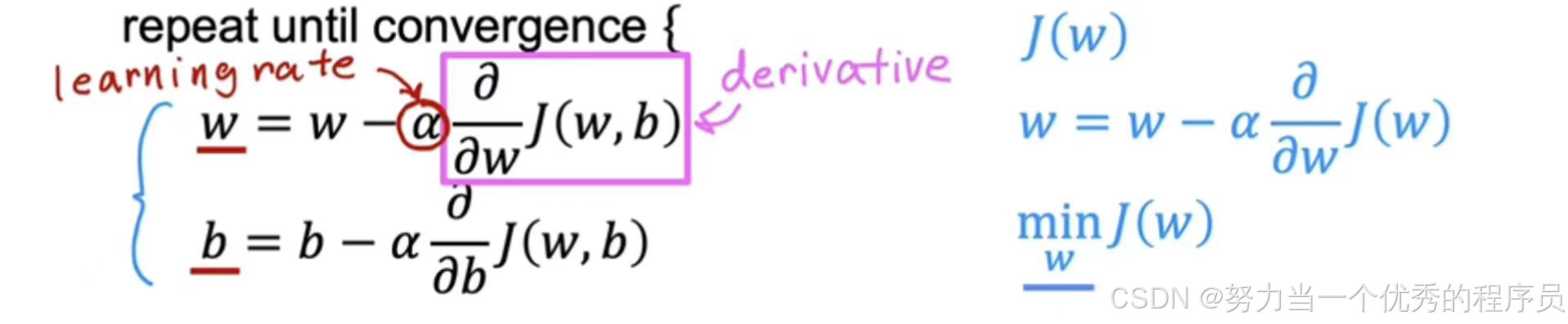

假设只有一个参数J（w），其中w是一个数字，这意味这梯度下降现在看起来像这样，你正在尝试通过调整参数w来最小化成本。

（1）像之前一样，我们暂时将b=0，可以查看成本函数J的二维图，让我们来看一下梯度下降对J（w）做了什么？

【例1】

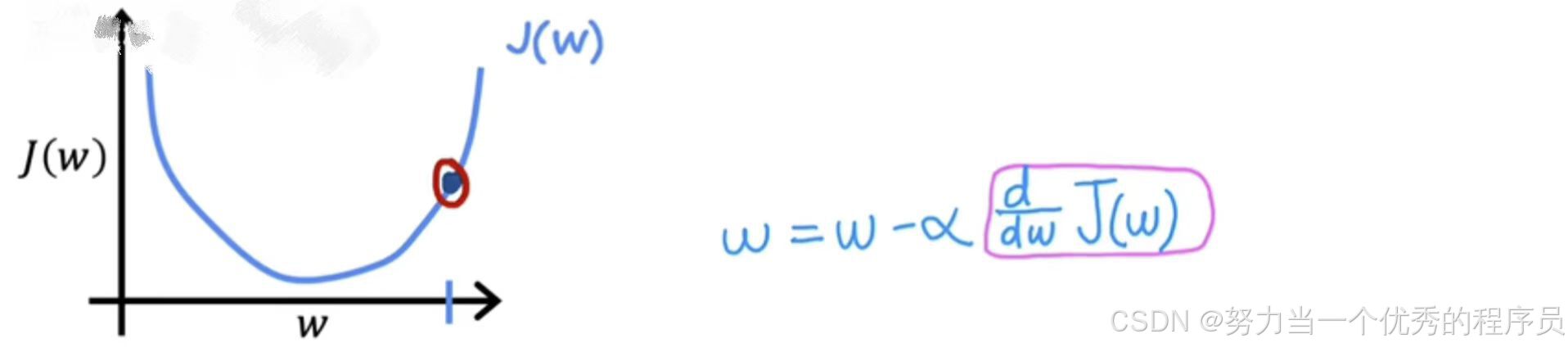
横轴：参数w，纵轴J（w）。现在较小初始化梯度下降，w有一些起始值，【如图】让我们在这个位置初始化它。想象一下，你从函数J（w）这一点开始，梯度下降将做的是将w更新为。

2.1.函数意义/计算：

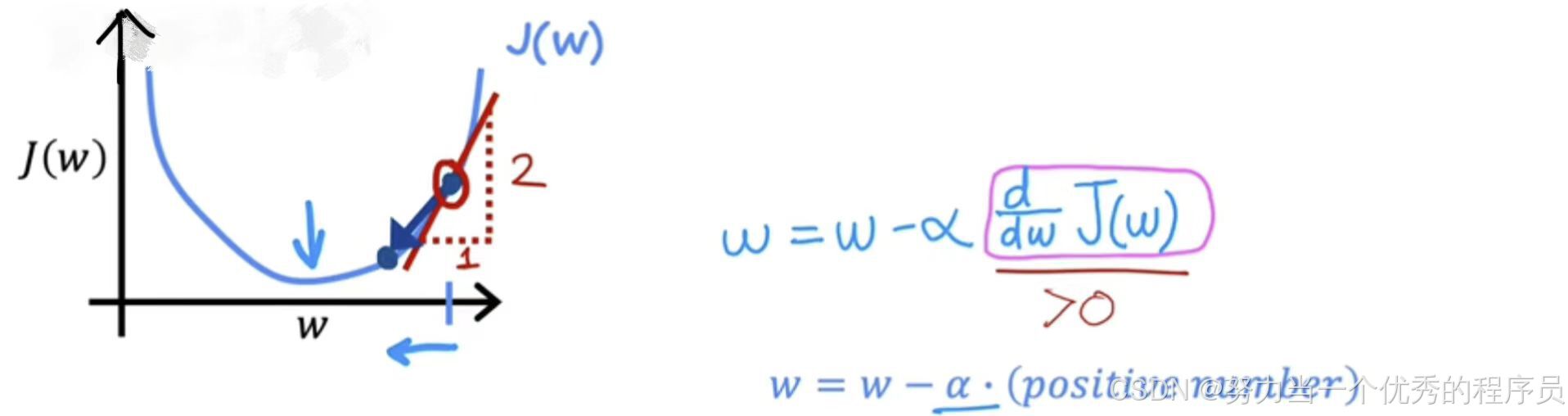
：考虑直线上这一点的导数的一种方法是画一条切斜，这是一条再改点与该曲线相交的直线。这条切线的斜率就是函数J在这一点上的导数。

为了得到斜率，可以画一个小三角形（与水平轴和垂直轴相交），计算小三角形高度除以三角形的宽度，就是斜率。例如：这个斜率可能是2:1；例如：当切斜指向上方和右侧时，斜率为正，这意味着该导数是正数，因此大于0。
：更新后的w将是w减去学习率乘以某个正数。学习率始终是正数，如果你用w减去一个正数，最终得到w的一个心智，会更小。在图表上，你正在向左移动，正在减小w的值，你可能会注意到。如果你的目标是降低成本J，这是正确的做法，因为当我们在这条曲线上向左移动式，成本J会降低，并且你会越来越接近J的最小值【如图所示】。到目前为止，梯度下降似乎在做正确的事。

【例2】采用与上面相同的J（w），现在假设在不同的位置初始化梯度下降。

例：在左边这里的w选择一个起始值，【如图所示】这一点是J，导数项，当我们做这里这一点切线时，这条线的斜率是J这一点的导数，这条向下向右倾斜的线具有负斜率（此时J的导数是负数）。比如，你画一个三角形，那么像这样的高是-2，宽是1，斜率是（-2/1）=-2就是负数。当你更新w是，你得到w减去学习率乘以一个负数，这意味着你从w中减去一个负数，但是减去一个负数意味着加上一个正数。所以最终会增加w，因为减去一个负数和加上一个正数是一样的。这一步梯度下降导致w增加，这意味着你正在向图表的右侧移动，你的成本J已经下降到【如图所示】。同样，看起来梯度下降正在做一些合理的事情，让你更接近最小值。

2.2.总结：

以上两个例子展示了导数项在做什么背后的一些直觉，以及为什么这个主体度下降改变w来让你更接近最小值。

3.学习率：

，α：学习率选择不当，下降率甚至可能不起作用。

<1>α太小或太大会发生什么？

α太小：
- 【如图所示】点开始下降，然后发生的事情是你将导数项乘以一个非常小的数字，所以最终会像那样迈出非常小的一步，如此往复，这过程结果是你最终确实降低了成本J，但速度非常慢，直到接近最小值。【如图所示】注意到你将需要很多步骤才能达到最小限度。总而言之，如果学习率太小，那么梯度下降会起作用，但速度会很慢，需要很长的时间。
α太大：
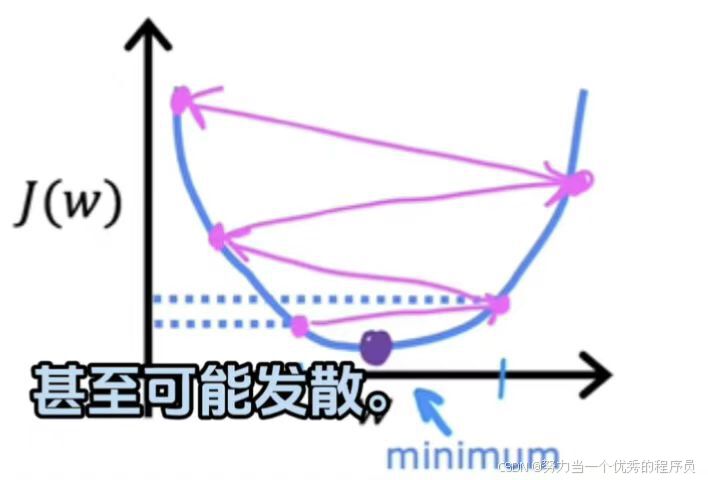
- 【如图所示】该点，它实际上已经非常接近最小值，如果学习率太大，那么更新w非常大一步，一直到【如图所示】，所以你从左边这个点一直移动到右边的这个点，而现在成本实际上变得更糟糕了，它增加，因为从左边值开始一步之后，实际上增加到右边的这个点处位置。现在这个新点的导数表示要减少w，但当学习率太大时，然后可能就会从起始点迈出一大步。如此往复，【如图所示】实际上离最小值越来越远。如果学习率太大，则会创建感觉可能会过冲，并且可能永远不会达到最小值。另一种说法是：大交叉可能无法收敛，甚至是可能发散。

<2>为什么梯度下降可以达到局部最小值，即使学习率α固定？

【例1】

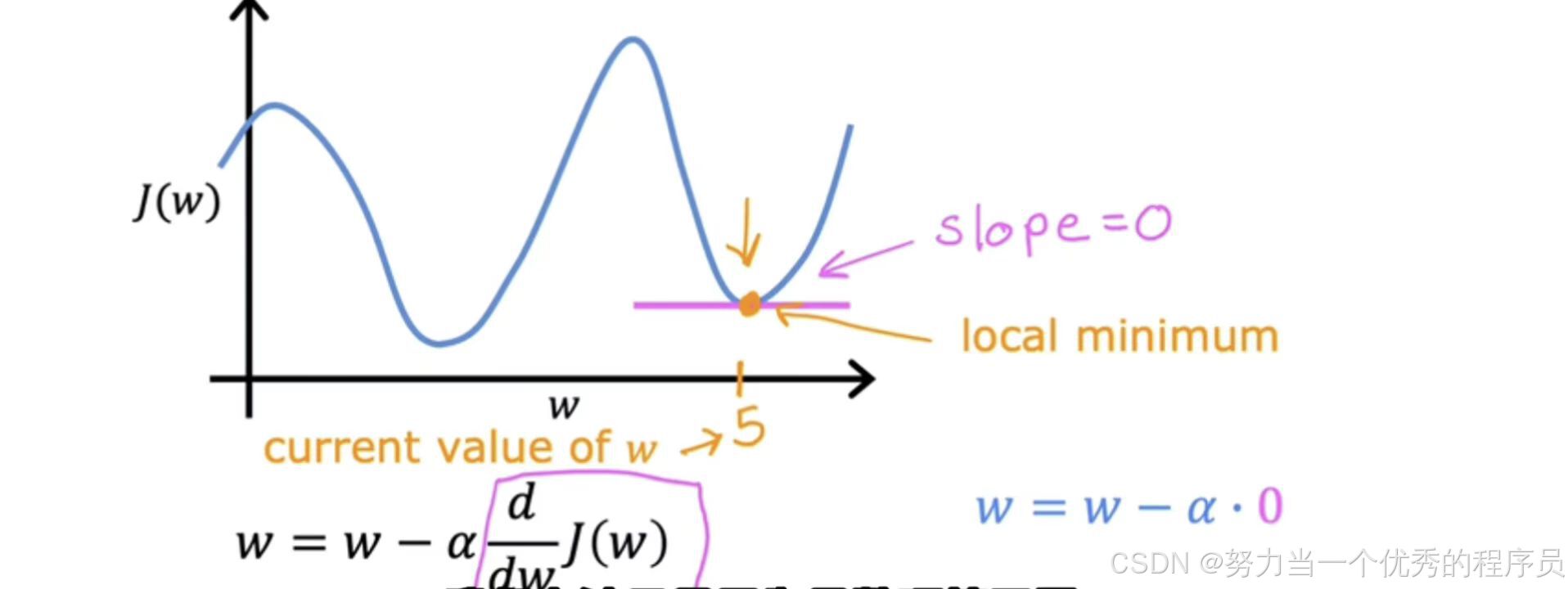
所以，另一个问题可能直到参数w之一已经存在【如图所示】此处，这样你的成本J已经处于局部最小值。如何认为，如果已经达到最小值，梯度下降的一步就可以了？
- 假设你有一些成本函数J，在这里看到的不是平方误差成本函数，这个成本函数有两个局部最小值，对应于你在这里看到的两个谷。现在让我们假设一些梯度下降步骤后，你的参数w在这结束，比如说=5，这就意味着你此时位于成本函数J上。恰好是局部最小值，如果你此时将注意力集中在该函数上，就会发现：这条线的斜率是0，因此导数项=0，所以，分级下降更新变成w=w-α*0=w。所以意味着：如果你已经处于局部最小值，梯度下降会使w保持不变。因为它只是将w的新值更新为与w的旧值完全相同。所以，具体来说，假设w的当前值为5，一次迭代后α为0.1，将w=w-α*0=5。一次，如果你的参数已经使你达到局部最小值，那么进一步的梯度下降步骤将完全没有，它不会更改你想要的参数，因为它将解决方案保持在局部最小值。

【例2】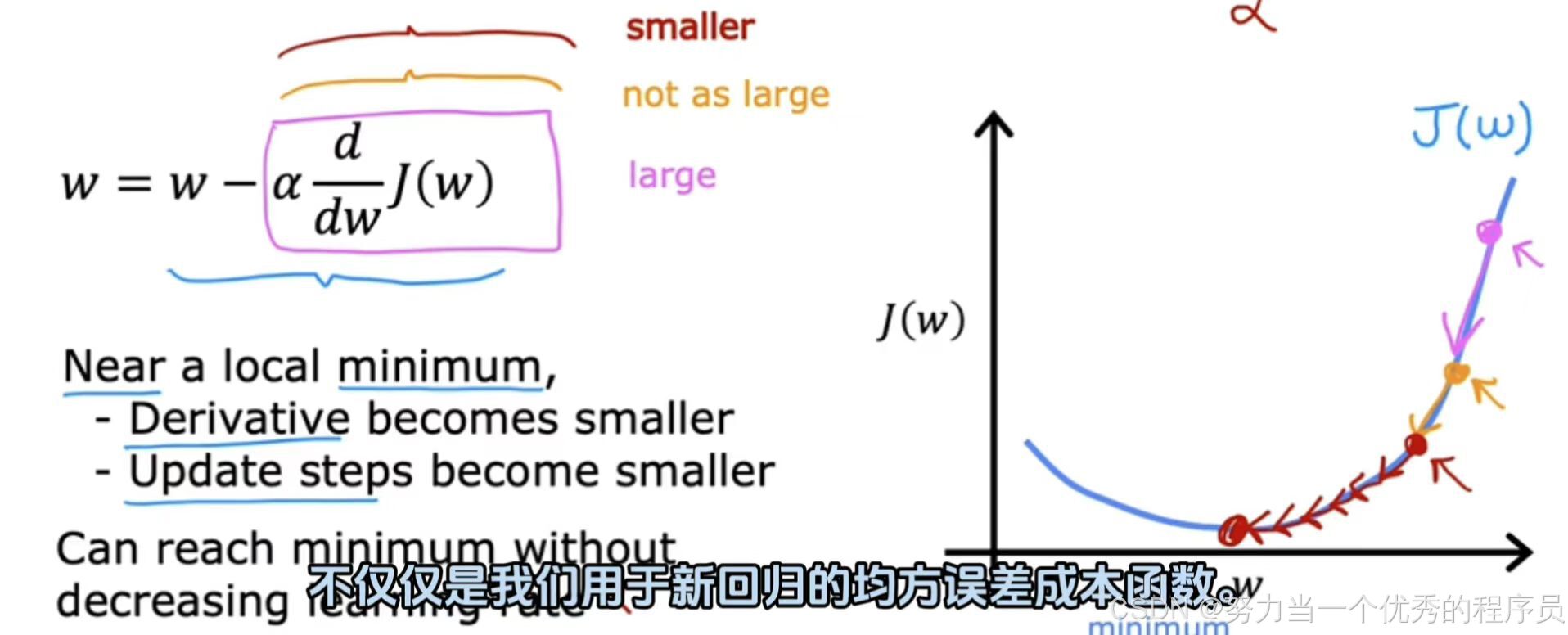

这是我们要最小化的J（w），现在【如图所示】在这里初始化梯度下降，如果我们采取一个更新步骤，允许它会把我们带到那一点，而且因为这个导数相当大，所以分级、下降就迈出了相对较大的一步；现在，我们正处于第二步，我们要迈出另一步，你可能会注意到坡度不像第一点那样陡峭，所以导数没有那么大，所以下一个更新步骤不会像第一步那么大；第三点，导数比上一点小，当我们接近最小值时，将采取更小的步骤，最终越来越接近0.因此，我们运行梯度下降时，最终会采取非常小的步骤，直到达到局部最小值。
所以，当我们接近局部最小梯度下降时，它会自动采取更小的步长。因为我们接近局部最小值时，导数会自动变小，意味着更新步骤也会自动变小。即使α保持在某个固定值。
这就是梯度下降算法，可以使用它来尝试最小化任何成本函数J，不仅仅用于新回归的均方误差成本函数。

4.线性回归中梯度下降：

4.1.作用：

使用平方误差成本函数来构建具有梯度下降的线性回归模型，将会使得我们能够训练线性回归模型以拟合一条直线来实现训练数据。

4.2.理解：

事实证明，如果计算这些导数，就会得到这些项（）。关于w的导数是：,然后是误差项，即预测值与实际值之差乘以输入特征值x^(i)。关于b的导数：。如果使用这些公式来计算这两个导数并以这种方式实现梯度下降，它将起作用。

4.3.推导过程：

这就是为什么我们必须在早些时候找到1.5的成本函数，因为它使偏导数更整洁，抵消了计算导数时出现的2，关于b的另一个导数，也是非常相似的。
，这就是线性回归梯度下降算法，重复对w和b执行这些更新，直到收敛。请记住，f(x)是一个线性回归模型，因此等于wx+b。
通常来说，凸函数【如图所示】是碗形函数，除了单个全局最小值之外，他不能有任何局部最小值。。当你在凸函数上实现梯度下降时，一个很好的特性是只要你选择适当的学习率，他总会收敛到全局最小值。

【注意】梯度下降是可以导致局部最小值而不是全局最小值，全局最小值时值所有可能点的成本函数J具有最低可能值的点。事实证明，当你使用线性回归的平方误差成本函数时，成本函数不会也永远不会有多个局部最小值。

5.运行梯度下降：

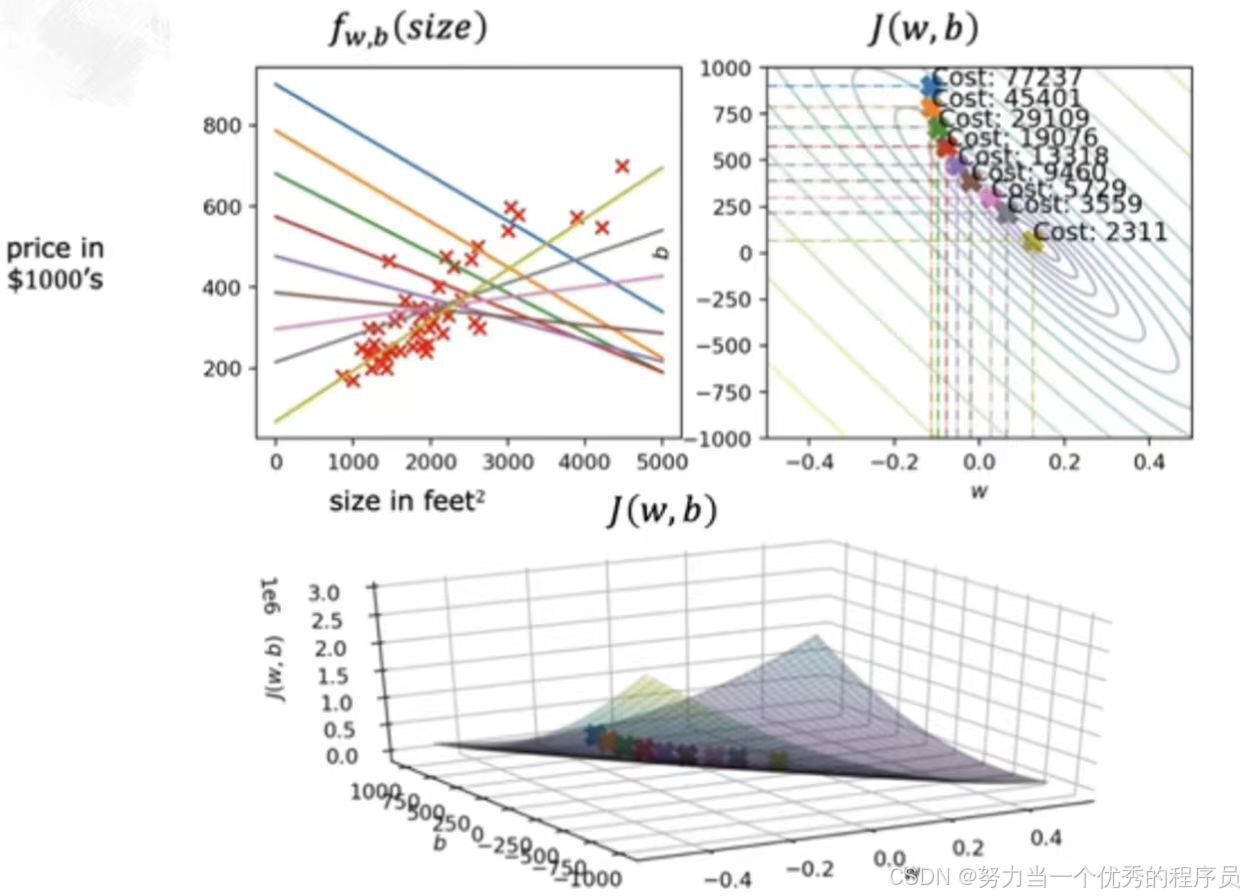
【如图所示】，左上角的模型和数据图，右上角是成本函数的等高线图，底部是相同的成本函数的曲面图。通常w和b都会初始化为0，但对于这个演示，让我们初始化w=-0.1和b=900，f（x）=-0.1x+900。现在，如果我们使用梯度下降迈出一步，我们最终会从成本函数的这一点向右下方移动到这一点，并注意到直线拟合也发生了一点变化。再走一步，成本函数现在移动，函数f（x）也发生变化。随着【如图所示】采取更多这些步骤，每次更新的成本都会降低。所以参数w和b遵循这个轨迹。【如图所示】左边，会得到相应的直线拟合，他会越来越适合数据，直到我们达到全局最小值。
这就是梯度下降，我们使用它来使模型适合持有的数据。现在可以使用f（x）模型来预测客户或其他任何人的房屋价格。例如：如果你朋友的房子面积是1250平方英尺，你现在可以读出价值并预测它们可能会得到250,000美元的房子。更准确地说，这个梯度下降过程被称为批量梯度下降过程。

批量梯度下降：术语bashed grading descent ，指的是梯度下降的每一步中，我们都在查看所有的训练示例，而不仅仅是训练数据的一个子集。所以在计算分级下降的时候，在计算导数的时候，i=1到m的和的时候。bash梯度下降在每次更新时查看整批训练示例。事实证明，其他版本的梯度下降不会查看整个训练集，而是在每个更新步骤查看训练数据的较小子集。但我们使用批量梯度下降，这就是线性回归。