Codeforces Round 859 (Div. 4)

---

A. Plus or Minus

time limit per test: 1 second memory limit per test: 256 megabytes input: standard input outputL: standard output

You are given three integers $a$, $b$, and $c$ such that exactly one of these two equations is true:

• $a+b=c$
• $a-b=c$

Output + if the first equation is true, and - otherwise.

Input

The first line contains a single integer $t$ ($1\le t\le 162$) — the number of test cases.

The description of each test case consists of three integers $a$, $b$, $c$ ($1\le a,b\le 9$, $-8\le c\le 18$). The additional constraint on the input: it will be generated so that exactly one of the two equations will be true.

Output

For each test case, output either + or - on a new line, representing the correct equation.

Example
input

11
1 2 3
3 2 1
2 9 -7
3 4 7
1 1 2
1 1 0
3 3 6
9 9 18
9 9 0
1 9 -8
1 9 10

output

+
-
-
+
+
-
+
+
-
-
+

Note

In the first test case, $1+2=3$.

In the second test case, $3-2=1$.

In the third test case, $2-9=-7$. Note that $c$ can be negative.

Tutorial
if 判断

Solution

for _ in range(int(input())):
    a, b, c = map(int, input().split())
    print("+" if a + b == c else "-")

---

B. Grab the Candies

time limit per test: 1 second memory limit per test: 256 megabytes input: standard input outputL: standard output

Mihai and Bianca are playing with bags of candies. They have a row $a$ of $n$ bags of candies. The $i$-th bag has $a_i$ candies. The bags are given to the players in the order from the first bag to the $n$-th bag.

If a bag has an even number of candies, Mihai grabs the bag. Otherwise, Bianca grabs the bag. Once a bag is grabbed, the number of candies in it gets added to the total number of candies of the player that took it.

Mihai wants to show off, so he wants to reorder the array so that at any moment (except at the start when they both have no candies), Mihai will have strictly more candies than Bianca. Help Mihai find out if such a reordering exists.

Input

The first line of the input contains an integer $t$ ($1\le t\le 1000$) — the number of test cases.

The first line of each test case contains a single integer $n$ ($1\le n\le 100$) — the number of bags in the array.

The second line of each test case contains $n$ space-separated integers $a_i$ ($1\le a_i\le 100$) — the number of candies in each bag.

Output

For each test case, output “YES” (without quotes) if such a reordering exists, and “NO” (without quotes) otherwise.

You can output the answer in any case (for example, the strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive answer).

Example
input

3
4
1 2 3 4
4
1 1 1 2
3
1 4 3

output

YES
NO
NO

Note

In the first test case, Mihai can reorder the array as follows: $[4,1,2,3]$. Then the process proceeds as follows:

• the first bag has $4$ candies, which is even, so Mihai takes it — Mihai has $4$ candies, and Bianca has $0$.
• the second bag has $1$ candies, which is odd, so Bianca takes it — Mihai has $4$ candies, and Bianca has $1$.
• the third bag has $2$ candies, which is even, so Mihai takes it — Mihai has $6$ candies, and Bianca has $1$.
• the fourth bag has $3$ candies, which is odd, so Bianca takes it — Mihai has $6$ candies, and Bianca has $4$.

Since Mihai always has more candies than Bianca, this reordering works.

Tutorial
偶数总和比奇数总和大就为 $YES$，因为可以先把偶数全部拿完，再去拿奇数

Solution

for _ in range(int(input())):
    n = int(input())
    a = list(map(int, input().split()))
    print("YES" if sum((x if x & 1 == 0 else 0) for x in a) > sum((x if x & 1 else 0) for x in a) else "NO")

---

C. Find and Replace

time limit per test: 1 second memory limit per test: 256 megabytes input: standard input outputL: standard output

You are given a string $s$ consisting of lowercase Latin characters. In an operation, you can take a character and replace all occurrences of this character with $\text{0}$ or replace all occurrences of this character with $\text{1}$.

Is it possible to perform some number of moves so that the resulting string is an alternating binary string${}^{†}$?

For example, consider the string $\text{abacaba}$. You can perform the following moves:

• Replace $\text{a}$ with $\text{0}$. Now the string is $\text{0}\text{b}\text{0}\text{c}\text{0}\text{b}\text{0}$.
• Replace $\text{b}$ with $\text{1}$. Now the string is $\text{0}\text{1}\text{0}\text{c}\text{0}\text{1}\text{0}$.
• Replace $\text{c}$ with $\text{1}$. Now the string is $\text{0}\text{1}\text{0}\text{1}\text{0}\text{1}\text{0}$. This is an alternating binary string.

${}^{†}$An alternating binary string is a string of $\text{0}$s and $\text{1}$s such that no two adjacent bits are equal. For example, $\text{01010101}$, $\text{101}$, $\text{1}$ are alternating binary strings, but $\text{0110}$, $\text{0a0a0}$, $\text{10100}$ are not.

Input

The input consists of multiple test cases. The first line contains an integer $t$ ($1\le t\le 100$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains an integer $n$ ($1\le n\le 2000$) — the length of the string $s$.

The second line of each test case contains a string consisting of $n$ lowercase Latin characters — the string $s$.

Output

For each test case, output “YES” (without quotes) if you can make the string into an alternating binary string, and “NO” (without quotes) otherwise.

You can output the answer in any case (for example, the strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive answer).

Example
input

8
7
abacaba
2
aa
1
y
4
bkpt
6
ninfia
6
banana
10
codeforces
8
testcase

output

YES
NO
YES
YES
NO
YES
NO
NO

Note

The first test case is explained in the statement.

In the second test case, the only possible binary strings you can make are $\text{00}$ and $\text{11}$, neither of which are alternating.

In the third test case, you can make $\text{1}$, which is an alternating binary string.

Tutorial
先把同一个字符的坐标存在一起，最后分别判断每一种字符的坐标的奇偶性是否一致，如果一致则为 $YES$，否则为 $NO$

Solution

for _ in range(int(input())):
    n = int(input())
    s = input()
    flag = True
    all = [[] for _ in range(26)]
    for i, c in enumerate(s):
        all[ord(c) - ord('a')].append(i)
    for a in all:
        for j, x in enumerate(a):
            if j and ((x & 1) ^ (a[j - 1] & 1)):
                flag = False
                break
        if not flag:
            break
    print("YES" if flag else "NO")

---

D. Odd Queries

time limit per test: 2 second memory limit per test: 256 megabytes input: standard input outputL: standard output

You have an array $a_1,a_2,\dots ,a_n$. Answer $q$ queries of the following form:

• If we change all elements in the range $a_l,a_{l+1},\dots ,a_r$ of the array to $k$, will the sum of the entire array be odd?

Note that queries are independent and do not affect future queries.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1\le t\le 10^4$). The description of the test cases follows.

The first line of each test case consists of $2$ integers $n$ and $q$ ($1\le n\le 2\cdot 10^5$; $1\le q\le 2\cdot 10^5$) — the length of the array and the number of queries.

The second line of each test case consists of $n$ integers $a_i$ ($1\le a_i\le 10^9$) — the array $a$.

The next $q$ lines of each test case consists of $3$ integers $l,r,k$ ($1\le l\le r\le n$; $1\le k\le 10^9$) — the queries.

It is guaranteed that the sum of $n$ over all test cases doesn’t exceed $2\cdot 10^5$, and the sum of $q$ doesn’t exceed $2\cdot 10^5$.

Output

For each query, output “YES” if the sum of the entire array becomes odd, and “NO” otherwise.

You can output the answer in any case (upper or lower). For example, the strings “yEs”, “yes”, “Yes”, and “YES” will be recognized as positive responses.

Example
input

2
5 5
2 2 1 3 2
2 3 3
2 3 4
1 5 5
1 4 9
2 4 3
10 5
1 1 1 1 1 1 1 1 1 1
3 8 13
2 5 10
3 8 10
1 10 2
1 9 100

output

YES
YES
YES
NO
YES
NO
NO
NO
NO
YES

Note

For the first test case:

• If the elements in the range $(2,3)$ would get set to $3$ the array would become { 2 , 3 , 3 , 3 , 2 } \{2, 3, 3, 3, 2\} {2,3,3,3,2}, the sum would be $2+3+3+3+2=13$ which is odd, so the answer is “YES”.
• If the elements in the range $(2,3)$ would get set to $4$ the array would become { 2 , 4 , 4 , 3 , 2 } \{2, 4, 4, 3, 2\} {2,4,4,3,2}, the sum would be $2+4+4+3+2=15$ which is odd, so the answer is “YES”.
• If the elements in the range $(1,5)$ would get set to $5$ the array would become { 5 , 5 , 5 , 5 , 5 } \{5, 5, 5, 5, 5\} {5,5,5,5,5}, the sum would be $5+5+5+5+5=25$ which is odd, so the answer is “YES”.
• If the elements in the range $(1,4)$ would get set to $9$ the array would become { 9 , 9 , 9 , 9 , 2 } \{9, 9, 9, 9, 2\} {9,9,9,9,2}, the sum would be $9+9+9+9+2=38$ which is even, so the answer is “NO”.
• If the elements in the range $(2,4)$ would get set to $3$ the array would become { 2 , 3 , 3 , 3 , 2 } \{2, 3, 3, 3, 2\} {2,3,3,3,2}, the sum would be $2+3+3+3+2=13$ which is odd, so the answer is “YES”.

Tutorial
利用前缀和，就可以将每个区间的和记录下来，然后对每次询问进行模拟

Solution

import sys
input = sys.stdin.readline

for _ in range(int(input())):
    n, q = map(int, input().split())
    a = [0] + list(map(int, input().split()))
    for i in range(1, n + 1):
        a[i] += a[i - 1]
    for __ in range(q):
        l, r, k = map(int, input().split())
        all = a[n] - (a[r] - a[l - 1]) + (r - l + 1) * k
        print("YES" if all & 1 else "NO")

---

E. Interview

time limit per test: 2 second memory limit per test: 256 megabytes input: standard input outputL: standard output

This is an interactive problem. If you are unsure how interactive problems work, then it is recommended to read the guide for participants.

Before the last stage of the exam, the director conducted an interview. He gave Gon $n$ piles of stones, the $i$-th pile having $a_i$ stones.

Each stone is identical and weighs $1$ grams, except for one special stone that is part of an unknown pile and weighs $2$ grams.

A picture of the first test case. Pile $2$ has the special stone. The piles have weights of $1,3,3,4,5$, respectively.

Gon can only ask the director questions of one kind: he can choose $k$ piles, and the director will tell him the total weight of the piles chosen. More formally, Gon can choose an integer $k$ ($1\le k\le n$) and $k$ unique piles $p_1,p_2,\dots ,p_k$ ($1\le p_i\le n$), and the director will return the total weight $m_{p_1}+m_{p_2}+\cdots +m_{p_k}$, where $m_i$ denotes the weight of pile $i$.

Gon is tasked with finding the pile that contains the special stone. However, the director is busy. Help Gon find this pile in at most $30$ queries.

Input

The input data contains several test cases. The first line contains one integer $t$ ($1\le t\le 1000$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($1\le n\le 2\cdot 10^5$) — the number of piles.

The second line of each test case contains $n$ integers $a_i$ ($1\le a_i\le 10^4$) — the number of stones in each pile.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$.

After reading the input for each test case, proceed with the interaction as follows.

Interaction

You can perform the operation at most $30$ times to guess the pile.

To make a guess, print a line with the following format:

• $\text{?}k{p}_1{p}_2{p}_3...p_{k-1}{p}_k$ ($1\le k\le n$; $1\le p_i\le n$; all $p_i$ are distinct) — the indices of the piles.

After each operation, you should read a line containing a single integer $x$ — the sum of weights of the chosen piles. (Formally, $x=m_{p_1}+m_{p_2}+\cdots +m_{p_k}$.)

When you know the index of the pile with the special stone, print one line in the following format: $\text{!}m$ ($1\le m\le n$).

After that, move on to the next test case, or terminate the program if there are no more test cases remaining.

If your program performs more than $30$ operations for one test case or makes an invalid query, you may receive a Wrong Answer verdict.

After you print a query or the answer, please remember to output the end of the line and flush the output. Otherwise, you may get Idleness limit exceeded or some other verdict. To do this, use the following:

• fflush(stdout) or cout.flush() in C++;
• System.out.flush() in Java;
• flush(output) in Pascal;
• stdout.flush() in Python;
• see the documentation for other languages.

It is additionally recommended to read the interactive problems guide for participants.

Hacks

To make a hack, use the following format.

The first line should contain a single integer $t$ ($1\le t\le 1000$) — the number of test cases.

The first line of each test case should contain two integers $n,m$ ($1\le n\le 2\cdot 10^5$) – the number of piles and the pile with the special stone.

The second line of each test case should contain $n$ integers $a_i$ ($1\le a_i\le 10^4$) — the number of stones in each pile.

Note that the interactor is not adaptive, meaning that the answer is known before the participant asks the queries and doesn’t depend on the queries asked by the participant.

Example
input

2
5
1 2 3 4 5

11

6

3

7
1 2 3 5 3 4 2

12

6

output

? 4 1 2 3 4

? 2 2 3

? 1 2

! 2

? 4 2 3 5 6

? 2 1 4

! 7

Note

In the first test case, the stone with weight two is located in pile $2$, as shown in the picture. We perform the following interaction:

• $\text{? 4 1 2 3 4}$ — ask the total weight of piles $1$, $2$, $3$, and $4$. The total weight we receive back is $1+3+3+4=11$.
• $\text{? 2 2 3}$ — ask the total weight of piles $2$ and $3$. The total weight we receive back is $3+3=6$.
• $\text{? 1 2}$ — ask the total weight of pile $2$. The total weight we receive back is $3$.
• $\text{! 2}$ — we have figured out that pile $2$ contains the special stone, so we output it and move on to the next test case.

In the second test case, the stone with weight two is located on index $7$. We perform the following interaction:

• $\text{? 4 2 3 5 6}$ — ask the total weight of piles $2$, $3$, $5$, and $6$. The total weight we receive back is $2+3+3+4=12$.
• $\text{? 2 1 4}$ — ask the total weight of piles $1$ and $4$. The total weight we receive back is $1+5=6$.
• $\text{! 7}$ — we have somehow figured out that pile $7$ contains the special stone, so we output it and end the interaction.

Tutorial
本题是道交互题，题意为：给出 $n$ 堆石子的数量，每个石子的重量都是 $1$，其中有一堆石子中的一个石子重量是 $2$，与机器交互找出那个石子在哪一堆
由于只有一堆有特殊的石子，即用二分查找即可逐渐向那一堆特殊石子靠近，最后剩下的一个就是答案

Solution

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define int long long

int ask(int l, int r) {
    cout << "? " << r - l + 1 << ' ';
    for (int i = l; i <= r; ++i) {
        cout << i << " \n"[i == r];
    }
    cout.flush();
    int x;
    cin >> x;
    return x;
}

void solve() {
    int n, y, mid, x;
    cin >> n ;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] += a[i - 1];
    }
    int l = 1, r = n;
    while (l < r) {
        int mid = (l + r) >> 1;
        int val = ask(l, mid);
        val -= a[mid] - a[l - 1];
        if (val) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    cout << "! " << l << endl;
    cout.flush();
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int test; cin >> test; while (test--)
    solve();
    return 0;
}

---

F. Bouncy Ball

time limit per test: 1 second memory limit per test: 256 megabytes input: standard input outputL: standard output

You are given a room that can be represented by a $n\times m$ grid. There is a ball at position $(i_1,j_1)$ (the intersection of row $i_1$ and column $j_1$), and it starts going diagonally in one of the four directions:

• The ball is going down and right, denoted by $\text{DR}$; it means that after a step, the ball’s location goes from $(i,j)$ to $(i+1,j+1)$.
• The ball is going down and left, denoted by $\text{DL}$; it means that after a step, the ball’s location goes from $(i,j)$ to $(i+1,j-1)$.
• The ball is going up and right, denoted by $\text{UR}$; it means that after a step, the ball’s location goes from $(i,j)$ to $(i-1,j+1)$.
• The ball is going up and left, denoted by $\text{UL}$; it means that after a step, the ball’s location goes from $(i,j)$ to $(i-1,j-1)$.

After each step, the ball maintains its direction unless it hits a wall (that is, the direction takes it out of the room’s bounds in the next step). In this case, the ball’s direction gets flipped along the axis of the wall; if the ball hits a corner, both directions get flipped. Any instance of this is called a bounce. The ball never stops moving.

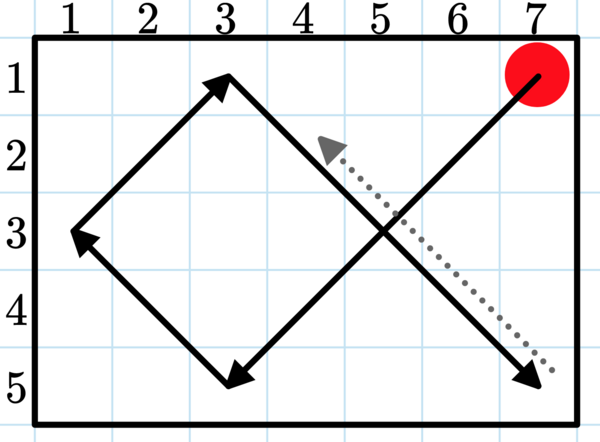
In the above example, the ball starts at $(1,7)$ and goes $\text{DL}$ until it reaches the bottom wall, then it bounces and continues in the direction $\text{UL}$. After reaching the left wall, the ball bounces and continues to go in the direction $\text{UR}$. When the ball reaches the upper wall, it bounces and continues in the direction $\text{DR}$. After reaching the bottom-right corner, it bounces once and continues in direction $\text{UL}$, and so on.

Your task is to find how many bounces the ball will go through until it reaches cell $(i_2,j_2)$ in the room, or report that it never reaches cell $(i_2,j_2)$ by printing $-1$.

Note that the ball first goes in a cell and only after that bounces if it needs to.

Input

The first line contains a single integer $t$ ($1\le t\le 1000$) — the number of test cases.

The first line of each test case contains six integers and a string $n,m,i_1,j_1,i_2,j_2,d$ ($2\le n,m\le 25000$; $1\le i_1,i_2\le n$; $1\le j_1,j_2\le m$; d ∈ { DR , DL , UR , UL } d \in\{ \texttt{DR}, \texttt{DL}, \texttt{UR}, \texttt{UL}\} d∈{DR,DL,UR,UL}) — the dimensions of the grid, the starting coordinates of the ball, the coordinates of the final cell and the starting direction of the ball.

It is guaranteed that the sum of $n\cdot m$ over all test cases does not exceed $5\cdot 10^4$.

Output

For each test case, output a single integer — the number of bounces the ball does until it reaches cell $(i_2,j_2)$ for the first time, or $-1$ if the ball never reaches the final cell.

Example
input

6
5 7 1 7 2 4 DL
5 7 1 7 3 2 DL
3 3 1 3 2 2 UR
2 4 2 1 2 2 DR
4 3 1 1 1 3 UL
6 4 1 2 3 4 DR

output

3
-1
1
-1
4
0

Tutorial
没有特殊处理，直接暴力模拟，模拟时注意边界问题

Solution

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define int long long

void solve() {
    int n, m, i1, j1, i2, j2, ans = 0;
    string d;
    cin >> n >> m >> i1 >> j1 >> i2 >> j2 >> d;
    for (int i = 0; i < 2 * n * m; i++) {
        if (i1 == i2 && j1 == j2) {
            cout << ans << endl;
            return;
        }
        bool b = 0;
        if (i1 == 1 && d[0] == 'U') {
            d[0] = 'D';
            b = 1;
        }
        if (i1 == n && d[0] == 'D') {
            d[0] = 'U';
            b = 1;
        }
        if (j1 == 1 && d[1] == 'L') {
            d[1] = 'R';
            b = 1;
        }
        if (j1 == m && d[1] == 'R') {
            d[1] = 'L';
            b = 1;
        }
        ans += b;
        i1 += (d[0] == 'U' ? -1 : 1);
        j1 += (d[1] == 'L' ? -1 : 1);
    }
    cout << "-1\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int test; cin >> test; while (test--)
    solve();
    return 0;
}

---

G2. Subsequence Addition (Hard Version)

time limit per test: 2 second memory limit per test: 256 megabytes input: standard input outputL: standard output

The only difference between the two versions is that in this version, the constraints are higher.

Initially, array $a$ contains just the number $1$. You can perform several operations in order to change the array. In an operation, you can select some subsequence${}^{†}$ of $a$ and add into $a$ an element equal to the sum of all elements of the subsequence.

You are given a final array $c$. Check if $c$ can be obtained from the initial array $a$ by performing some number (possibly 0) of operations on the initial array.

${}^{†}$ A sequence $b$ is a subsequence of a sequence $a$ if $b$ can be obtained from $a$ by the deletion of several (possibly zero, but not all) elements. In other words, select $k$ ($1\le k\le |a|$) distinct indices $i_1,i_2,\dots ,i_k$ and insert anywhere into $a$ a new element with the value equal to $a_{i_1}+a_{i_2}+\cdots +a_{i_k}$.

Input

The first line of the input contains an integer $t$ ($1\le t\le 1000$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($1\le n\le 2\cdot 10^5$) — the number of elements the final array $c$ should have.

The second line of each test case contains $n$ space-separated integers $c_i$ ($1\le c_i\le 2\cdot 10^5$) — the elements of the final array $c$ that should be obtained from the initial array $a$.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$.

Output

For each test case, output “YES” (without quotes) if such a sequence of operations exists, and “NO” (without quotes) otherwise.

You can output the answer in any case (for example, the strings “yEs”, “yes”, “Yes” and “YES” will be recognized as a positive answer).

Example
input

6
1
1
1
2
5
5 1 3 2 1
5
7 1 5 2 1
3
1 1 1
5
1 1 4 2 1

output

YES
NO
YES
NO
YES
YES

Note

For the first test case, the initial array $a$ is already equal to $[1]$, so the answer is “YES”.

For the second test case, performing any amount of operations will change $a$ to an array of size at least two which doesn’t only have the element $2$, thus obtaining the array $[2]$ is impossible and the answer is “NO”.

For the third test case, we can perform the following operations in order to obtain the final given array $c$:

• Initially, $a=[1]$.
• By choosing the subsequence $[1]$, and inserting $1$ in the array, $a$ changes to $[1,1]$.
• By choosing the subsequence $[1,1]$, and inserting $1+1=2$ in the middle of the array, $a$ changes to $[1,2,1]$.
• By choosing the subsequence $[1,2]$, and inserting $1+2=3$ after the first $1$ of the array, $a$ changes to $[1,3,2,1]$.
• By choosing the subsequence $[1,3,1]$ and inserting $1+3+1=5$ at the beginning of the array, $a$ changes to $[5,1,3,2,1]$ (which is the array we needed to obtain).

Tutorial
由题意得，对题目给出的字符串排序后，前两个元素必定是 $1$，后面的元素都不能比之前元素的和还要大，否则就不能凑出来，所以只需要对数组排序后，从前往后遍历判断即可

Solution

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define int long long

void solve() {
    int n, cnt;
    cin >> n;
    vector<int> c(n);
    for (int &ci : c) {
        cin >> ci;
    }
    ranges::sort(c);
    if (n < 3) {
        cout << (accumulate(c.begin(), c.end(), 0ll) == n ? "YES\n" : "NO\n");
        return;
    }
    if ((cnt = c[0] + c[1]) != 2) {
        cout << "NO\n";
        return;
    }
    for (int i = 2; i < n; ++i) {
        if (c[i] > cnt) {
            cout << "NO\n";
            return;
        }
        cnt += c[i];
    }
    cout << "YES\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int test; cin >> test; while (test--)
    solve();
    return 0;
}