本文包含线性代数中的简算题、计算题及证明题。涉及排列的逆序数计算、行列式的计算、矩阵变换求逆矩阵、克莱姆法则解方程组、非齐次方程组的解及其基础解系、向量运算等内容。
一、简算题
1
、按自然数从小到大为标准次序，求下列各排列的逆序数：（
5
分）
1 3 ...
(2
n
-
1) 2 4
...
(2
n
)
2
、计算下列行列式：（
10
分）
3、试利用矩阵的初等变换，求下列方阵的逆矩阵：
二、计算题
1
、用克莱姆法则解方程组．
2
、求以下非齐次方程组的一个解及对应的齐次线性方程组的基础解系：
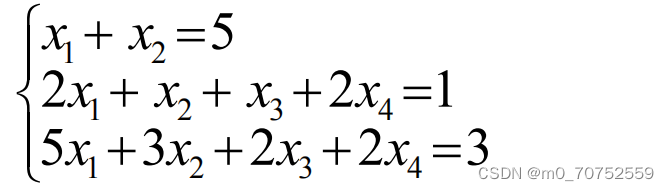
3、设 v1=(1, 1, 0)T, v2=(0, 1, 1)T, v3=(3, 4, 0)T, 求 v1-v2及 3v1+2v2-v3．
三、证明题
1、 
2、由
a
1
=
(0
,
1
,
1)
T
,
a
2=
(1
,
0
,
1)
T
,
a
3
=
(1
,
1
,
0)
T
所生成的向量空间就是
R
3
.
3
、举例说明下列命题是错误的
:
若向量组
a
1
,
a
2
, ...，
a
m
是线性相关的
，
则
a
1
可由
a
2，...
，
a
m
线性表示
。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
