数学知识——组合计数

排列数

从n个不同的元素中取出m个元素组成一列，产生的不同排列的数量。

$A_n^m=\frac{n!}{(n-m)!}$

怎么得来的？先选一个元素，选法为$n$,选第二个元素，选法为$n-1$，以此类推，选第$m$个元素，选法为$n-m+1$,相乘即为$A_n^m=\frac{n!}{(n-m)!}$。

组合数

从n个不同的元素中取出m个组成一个集合（不考虑顺序），产生不同集合数量。
根据数据范围不同，求组合数有四种方法。

递推

$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$ 证明：
我们可以把选择的方案分成两大类，对于$a$个数里面的某个数，我可能选出来了，也可能没选出来
选出来了：$C_{a-1}^{b-1}$，还需要在剩下的$a-1$个数选$b-1$个。
没选出来：$C_{a-1}^b$需要在剩下的$a-1$个数选$b$个。

给定 $n$ 组询问，每组询问给定两个整数 $a，b$，请你输出 $C_b^{a}mod(10^9+7)$的值。

$1\le n\le 10000,$
$1\le b\le a\le 2000$

先利用地推求出所有的$C_a^b$，时间复杂度为$O(K^2)$，接下来对于每一个询问都可以在$O(1)$时间复杂度内回答，总的时间复杂度为$O(K^2+N)$。

void init()
{
    for (int i = 0; i <= 2000; i ++ )
        for (int j = 0; j <= i; j ++ )
        {
            if (j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
}
int main()
{
    cin >> n;
    init();
    while (n -- )
    {
        int a, b;
        cin >> a >> b;
        cout << c[a][b] << endl;
    }
    return 0;
}

预处理

$C_a^b=\frac{a!}{b!(a-b)!}$（在$A_a^b$的基础上多除一个$b!$）

给定 $n$ 组询问，每组询问给定两个整数 $a，b$，请你输出 $C_b^{a}mod(10^9+7)$的值。

$1\le n\le 10000,$
$1\le b\le a\le 10^5$

用$fact[i]$表示$a!$,用$infact[i]$表示$a!$的逆元。
$fact[i]=fact[i-1]\ast i\%p$
$infact[i]=infact[i-1]\ast qmi(i,p-2,p)\%p$

时间复杂度为$O(KlogP+N)$

int qmi(int a, int k, int m)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll) res * a % mod;
        k >>= 1;
        a = (ll) a * a % mod;
    }
    return res;
}
int main()
{
    cin >> n;
    fact[0] = infact[0] = 1;
    for (int i = 1; i <= 100000; i ++ ) 
    {
        fact[i] = fact[i - 1] * i % mod;
        infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    while (n -- )
    {
        int a, b;
        cin >> a >> b;
        cout << fact[a] * infact[a - b] % mod * infact[b] % mod << endl;
    }
    return 0;
}

lucas定理

$C_a^b\equiv C_{a\%p}^{b\%p}{C}_{a/p}^{b/p}(modp)$
证明：

给定 $n$ 组询问，每组询问给定两个整数 $a，b$，请你输出 $C_b^{a}modp$的值。

$1\le n\le 20$
$1\le b\le a\le 10^{18}$
$1\le p\le 10^5$

时间复杂度为$O(Nlo{g}_P^{K}PlogP)$
$N$为数据规模
$lo{g}_P^K$为$lucas$的递归次数
$P$为求$C_{a\%p}^{b\%p}$的过程中的循环次数，因为$a,b$都进行了对$p$的取模，所以求阶乘的规模就在$O(P)$
$logP$为qmi的复杂度

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll) res * a % p;
        k >>= 1;
        a = (ll) a * a % p;
    }
    return res;
}
int c(ll a, ll b, int p)
{
    int res = 1;
    for (int i = 1, j = a; i <= b; i ++ , j -- )
    {
        res = (ll) res * j % p;
        res = (ll) res * qmi(i, p - 2, p) % p;
        cout << res << endl;
    }
    cout << endl;
    return res;
}
int lucas(ll a, ll b, int p)
{
    if (b < p && a < p) return c(a, b, p);
    else return (ll) c(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
    cin >> n;
    while (n -- )
    {
        ll a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }
    return 0;
}

分解质因数

给定两个整数 $a，b$，请你输出 $C_b^a$的值。
注意结果可能很大，需要使用高精度计算。

$1\le b\le a\le 5000$

1.先筛选出$a$以内的所有素数
2.我们对$a!$分解质因数,其中包含的质数$p$的个数为$\lfloor \frac{a}{p}\rfloor +\lfloor \frac{a}{p^2}\rfloor +\lfloor \frac{a}{p^3}\rfloor +...$。$C_a^b$分解的结果中某个质因数的个数其实是$a!$中这个质数的个数减去$b!$和$(a-b)!$中这个质数的个数。
3.我们得到了$C_a^b$每个质因数的个数，可以直接使用高精度乘法求解。

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = 1;
            if (i % primes[j] == 0) break; 
        }
    }
}
int get(int a, int p)
{
    int res = 0;
    while (a)
    {
        res += a / p;
        a /= p;
    }
    return res;
}
vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}
int main()
{
    int a, b;
    cin >> a >> b;
    get_primes(a);
    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] += get(a, p) - get(a - b, p) - get(b, p);
    }
    vector<int> res;
    res.push_back(1);
    for (int i = 0; i < cnt; i ++ )
        for (int j = 1; j <= sum[i]; j ++ )
        {
            res = mul(res, primes[i]);
        }
    for (int i = res.size() - 1; i >= 0; i -- )
        cout << res[i];
    puts("");
    return 0;
}

可以做一些数学题感受一下
q1.由$0,1,2,3,4,5$可以组成多少个没有重复数字的五位奇数。
特殊位置优先，先考虑末尾以及首位，末尾只能放$1,3,5$,首位不能放$0$,答案为$C_3^1\ast C_4^1\ast A_3^3$

q2.$7$ 人站成一排，其中甲乙相邻且丙丁相邻，共有多少种不同的排法。
我们可以先将甲乙，丙丁分别看成是一个人，这时候的方案数为然后在考虑甲乙，丙丁内部的方案数，各为$A_2^2$
总方案数为$A_5^5\ast A_2^2\ast A_2^2$

q3.$8$人排成前后两排，每排$4$人，其中甲乙在前排，丙在后排，共有多少排法。
$A_4^1\ast A_4^2\ast A_5^5$

q4.有$5$个不同的小球,装入$4$个不同的盒内，每盒至少装一个球，求共有多少不同的装法。
$5$个里面选$2$个捆绑起来,最后把$4$个元素做全排列。
$C_5^2\ast A_4^4$

q5.6个人站成一列拍照，甲乙相邻，丙丁不相邻的方案数。
$2A_5^5-4A_4^4$

卡特兰数

在一个二维平面内，从(0, 0)出发到达(n, n)，每次可以向上或者向右走一格，0代表向右走一个，1代表向上走一格，则每条路径都会代表一个01序列，则满足任意前缀中0的个数不少于1个数序列对应的路径则右下侧

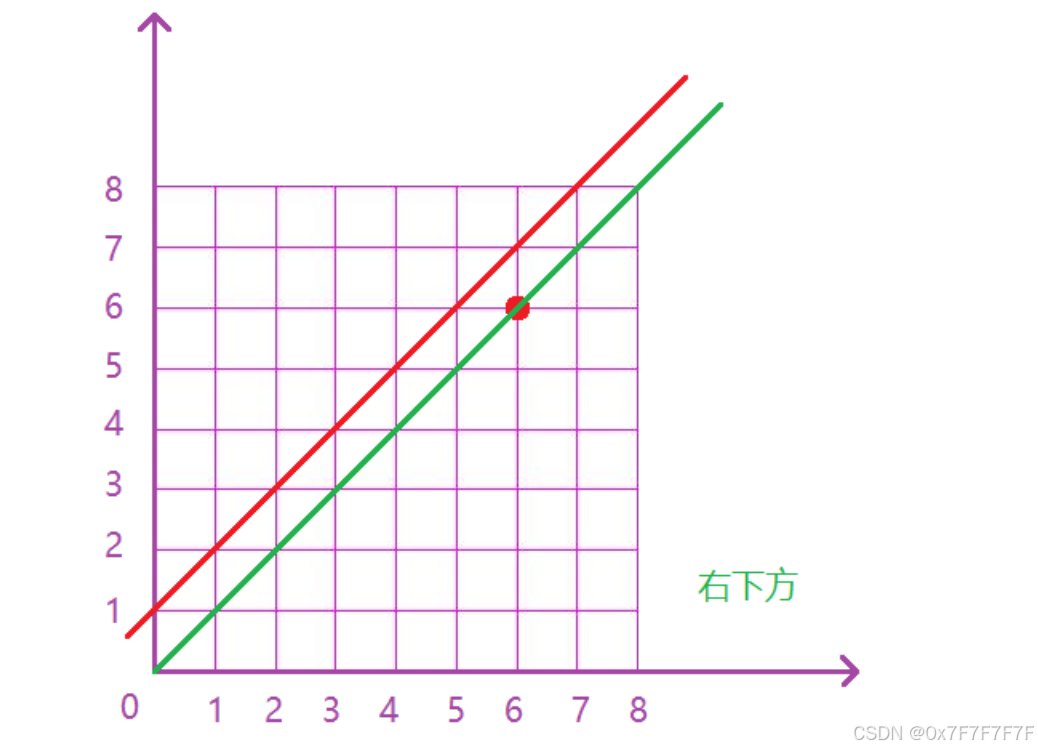
符合要求的路径必须严格在上图中红色线的下面（不可以碰到图中的红线，可以碰到绿线）。则我们考虑任意一条不合法路径，例如下图：

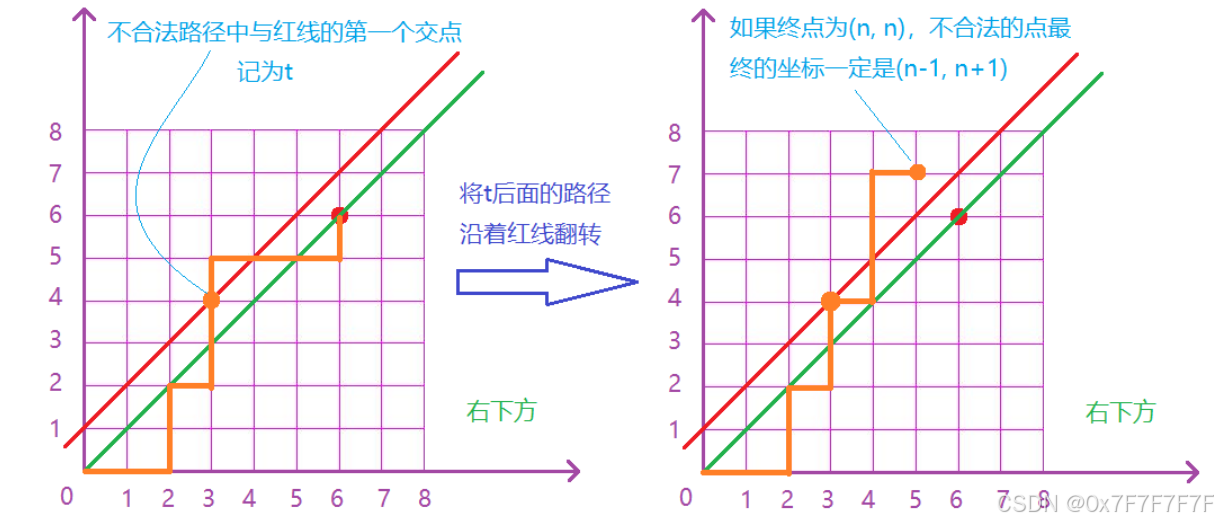
所有路径的条数为 $C_{2n}^n$，其中不合法的路径有 $C_{2n}^{n-1}$ 条，因此合法路径有：
$C_{2n}^n-C_{2n}^{n-1}$
$=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}$
$=\frac{(2n)!}{n!n!}-\frac{n}{n+1}\frac{(2n)!}{n!n!}$
$=\frac{1}{n+1}\frac{(2n)!}{n!n!}$
$=\frac{1}{n+1}{C}_{2n}^n$

例题

牡牛和牝牛

约翰要带 $N$ 只牛去参加集会里的展示活动，这些牛可以是牡牛，也可以是牝牛。

牛们要站成一排，但是牡牛是好斗的，为了避免牡牛闹出乱子，约翰决定任意两只牡牛之间至少要有 $K$ 只牝牛。

请计算一共有多少种排队的方法，所有牡牛可以看成是相同的，所有牝牛也一样，答案对 $5000011$ 取模。

输入格式
一行，输入两个整数 $N$ 和 $K$。

输出格式

一个整数，表示排队的方法数。

数据范围
$1\le N\le 10^5,$
$0\le K<N$

输入样例：

4 2

输出样例：

6

样例解释

6

种方法分别是：牝牝牝牝，牡牝牝牝，牝牡牝牝，牝牝牡牝，牝牝牝牡，牡牝牝牡。

$f[i]$集合：考虑前$i$头牛，且第$i$头牛是$1$的方案
$f[i]$属性：方案数
状态计算：$f[i]=f[i-k-1]+f[i-k-2]+\cdot \cdot \cdot +f[0]$
(↑集合划分的依据是题目的要求，即当前1与上一个1之间至少要间隔k个0)

此处设置一个边界$f[0]$表示只有0没有1的边界情况

#include <iostream>
using namespace std;
const int N = 100010;
const int mod = 5000011;
int s[N], f[N];
int n, k;
int main()
{
    cin >> n >> k;
    s[0] = f[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = s[max(i - k - 1, 0)];
        s[i] = (s[i - 1] + f[i]) % mod;
    }
    cout << s[n] << endl;
    return 0;
}

方程的解

佳佳碰到了一个难题，请你来帮忙解决。

对于不定方程 $a_1+a_2+\cdots +a_{k-1}+a_k=g(x)$，其中 $k\ge 1$
且 $k\in N\ast ，x$ 是正整数，$g(x)=x^{x}mod1000$
（即 $x^x$ 除以 1000 的余数），$x,k$ 是给定的数。

我们要求的是这个不定方程的正整数解组数。

举例来说，当 $k=3,x=2$ 时，方程的解分别为：
$\{\begin{array}{l}{a}_1=1\\ a_2=1\\ a_3=2\end{array},\{\begin{array}{l}{a}_1=1\\ a_2=2\\ a_3=1\end{array},\{\begin{array}{l}{a}_1=2\\ a_2=1\\ a_3=1\end{array}$

输入格式

有且只有一行，为用空格隔开的两个正整数，依次为 $k,x$。

输出格式

有且只有一行，为方程的正整数解组数。

数据范围
$1\le k\le 100,$
$1\le x<2^{31}$,
$k\le g(x)$

输入样例：

3 2

输出样例：

3

对$n=x^x$进行快速幂求解，接下来利用隔板法来求解的组数。
一种隔板法的情况和一组解时一一对应的，例如$n=7,k=4$时，
$\ast \ast |\ast \ast |\ast \ast |\ast$就是唯一对应一组解$a_1=2,a_2=2，a_3=2,a_4=1$，$a_1=2,a_2=2.a_3=2,a_4=1$，也唯一对应一种隔板法情况$\ast \ast |\ast \ast |\ast \ast |\ast$。
方案总数为$C_{n-1}^{k-1}$。

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 150;
int c[1010][110][N];
int k, x;
void add(int a[], int b[], int c[])
{
    for (int i = 0, t = 0; i < N; i ++ )
    {
        t += b[i] + c[i];
        a[i] = t % 10;
        t /= 10;
    }
}
int qmi(int a, int k, int b)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll)res * a % b;
        a = (ll)a * a % b;
        k >>= 1;
    }
    return res;
}
int main()
{
    cin >> k >> x;
    int n = qmi(x, x, 1000);
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j <= min(i, k - 1); j ++ )
        {
            if (j == 0) c[i][j][0] = 1;
            else add(c[i][j], c[i - 1][j], c[i - 1][j - 1]);
        }
    }
    int pos = N - 1;
    while (c[n - 1][k - 1][pos] == 0) pos -- ;
    while (pos >= 0) cout << c[n - 1][k - 1][pos -- ];
    return 0;
}

车的放置

有下面这样的一个网格棋盘，$a,b,c,d$ 表示了对应边长度，也就是对应格子数。

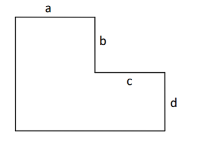
当 $a=b=c=d=2$时，对应下面这样一个棋盘：

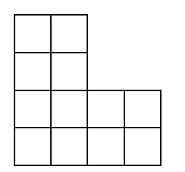
要在这个棋盘上放 $k$ 个相互不攻击的车，也就是这 $k$ 个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。

只需要输出答案 $mod100003$ 后的结果。

输入格式

共一行，五个非负整数 $a,b,c,d,k$。

输出格式

包括一个正整数，为答案 $mod100003$ 后的结果。

数据范围
$0\le a,b,c,d,k\le 1000$，保证至少有一种可行方案。

输入样例：

2 2 2 2 2

输出样例：

38

如果我们面对的是一个$n\times m$的矩形的话，考虑放置$k$个车的方案数。
因为同一行肯定不能放两个，所以第一步是在$n$行里面选择$k$行放置，即$C_n^k$，对于这$k$行，不同的排列方案数为$m\ast (m-1)\ast ...\ast (m-k+1)$，即$P_m^k$，最终答案为$C_n^k\ast P_m^k$。
考虑题目中的图，我们考虑先在上面的小矩形里面放$i$个车，即$C_b^i\ast P_a^i$，余下的$k-i$个车放下面的矩形里，即$C_d^{k-i}\ast P_{a+c-i}^{k-i}$。
最终答案为$C_n^k\ast P_m^k\ast C_d^{k-i}\ast P_{a+c-i}^{k-i}$。
在$O(nlogm)$预处理出$fact[i]$和$infact[i]$之后，可以直接在$O(1)$的时间复杂度求出答案。

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 2010;
const int mod = 100003;
int fact[N], infact[N];
int c[N][N];
int qmi(int a, int k, int b)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll)res * a % b;
        a  = (ll)a * a % b;
        k >>= 1;
    }
    return res;
}
int C(int a , int b)
{
    if(a < b) return 0;
    return (ll)fact[a] * infact[b] % mod  * infact[a-b] % mod;
}

int P(int a , int b)
{
    if(a < b) return 0;
    return (ll)fact[a] * infact[a - b] % mod;
}
int main()
{
    int a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++ )
    {
        fact[i] = (ll)fact[i - 1] * i % mod;
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    int res = 0;
    for (int i = 0; i <= b; i ++ )
    {
        res = (res + (ll)C(b, i) * C(d, k - i) % mod * P(a, i) % mod * P(a + c - i, k - i)) % mod;
    }
    cout << res << endl;
    return 0;
}

数三角形

给定一个 $n\times m$ 的网格，请计算三点都在格点上的三角形共有多少个。

下图为 $4\times 4$ 的网格上的一个三角形。

注意：三角形的三点不能共线。

输入格式
输入一行，包含两个空格分隔的正整数 $m$ 和 $n$。

输出格式
输出一个正整数，为所求三角形数量。

数据范围
$1\le m,n\le 1000$

输入样例：

2 2

输出样例：

76

考虑反着求，即先求出来任选三点的方案总数，减去不合法的方案数。
任选三点的方案总数为$C_{(n+1)(m+1)}^3$
不合法的方案数分为以下三种情况：
1.三点构成的直线斜率为0，这样的情况总数为$(n+1)C_{m+1}^3$
2.三点构成的直线斜率不存在，这样的情况总数为$(m+1)C_{n+1}^3$
3.三点构成的直线斜率为正或为负，这两种情况方案总数是一样的，也正因此只需要考虑为正的情况，最后把结果乘2。

考虑枚举斜线的高度$i$和宽度$j$，这样可以唯一确定一个直角三角形的形状，这样的三角形在方格图中有$(n-i)\ast (m-j)$个放置位置，斜边的两个端点为其中两个点，第三个点的位置为这条斜线上的整数坐标位置，这样的位置总数为$gcd(i,j)-1$。

第三种情况不合法的方案数为${\sum }_{i\le n,j\le m}2\ast (n-i)\ast (m-j)\ast (gcd(i,j)-1)$，求解的时间复杂度为$O(n^{2}logn)$。

最终答案为$C_{(n+1)(m+1)}^3-(n+1)C_{m+1}^3-(m+1)C_{n+1}^3-{\sum }_{i\le n,j\le m}2\ast (n-i)\ast (m-j)\ast (gcd(i,j)-1)$。

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 1010;
int n, m;
ll C(int x)
{
    return (ll)x * (x - 1) * (x - 2) / 6;
}
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int main()
{
    cin >> n >> m;
    ll res = C((n + 1) * (m + 1)) - (m + 1) * C(n + 1) - (n + 1) * C(m + 1);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            res -= 2 * (n - i + 1) * (m - j + 1) * (gcd(i, j) - 1);
    cout << res << endl;
    return 0;
}

序列统计

给定三个整数 $N,L,R$，统计长度在 $1$ 到 $N$ 之间，元素大小都在 $L$到 $R$之间的单调不降序列的数量。

输出答案对 $10^6+3$ 取模的结果。

输入格式

输入第一行包含一个整数 $T$，表示数据组数。
第二到第 $T+1$ 行每行包含三个整数 $N,L,R$。

输出格式

输出包含 $T$ 行，每行有一个数字，表示你所求出的答案对 $10^6+3$ 取模的结果。

数据范围
$0\le N,L,R\le 10^9,$
$1\le T\le 100，$
输入数据保证 $L\le R$。

输入样例：

2
1 4 5
2 4 5

输出样例：

2
5

样例解释
对于第一组输入，满足条件的两个序列为 $4,5$。

元素大小在$L$到$R$,将其映射为$0$到$R-L$之间，该问题就等价于对于$0\le a_1\le a_2\le ...\le a_k\le R-L$，求出$a_i$合法解的总数

法1：直接对这个问题求解较为困难，我们先考虑下面这个问题：
对于$x\le b_1<b_2<...<b_k\le y$，我们想要求合法的$b_i$的解的组数，答案就是在$x$到$y$范围内选择出$k$的数的方案总数，即$C_{y-x+1}^k$，考虑能不能把本问题的场景转化为这个可以解决的问题。令$c_i=a_i+i-1$，这样一来问题转化为$0\le c_1<c_2<...<c_k\le R-L+k-1$解的组数，即$C_{R-L+k}^k$。
法2：令$b_1=a_1,b_2=a_2-1_1,...,b_k=a_k-a_{k-1}$，这样问题就转化为求满足条件$0\le b_1+b_2+...+b_k\le R-L$的$b_i$的解的组数,联想隔板法，一般的隔板法解决的是解为正整数的情况，但是本问题中$b_i$的取值是非负数，考虑令$c_i=b_i+1$，这样一来把问题转化为求满足条件$k\le c_1+c_2+...+c_k\le R-L+k$的$c_i$的解的组数,传统隔板法要求的是何为定值的情况，这里却要求小于等于一个值的情况，考虑加入$k$个隔板而不是$k-1$个，这样前$k$个隔内的数量就是问题的一组解，最后一个隔就是没有选的数，最终结果为$C_{R-L+k}^k$。

法1和法2都得到了相同的结果，本问题最终要求的是${\sum }_{i=1}^k{C}_{R-L+i}^i$。${\sum }_{i=1}^k{C}_{R-L+i}^i=C_{R-L+1}^1{C}_{R-L+2}^2+...+C_{R-L+k}^k=C_{R-L+1}^{R-L}+C_{R-L+2}^{R-L}+...+C_{R-L+k}^{R-L}=C_{R-L+1}^{R-L+1}+C_{R-L+1}^{R-L}+C_{R-L+2}^{R-L}+...+C_{R-L+k}^{R-L}-C_{R-L+1}^{R-L+1}=C_{R-L+2}^{R-L+1}+C_{R-L+2}^{R-L}+...+C_{R-L+k}^{R-L}-1=C_{R-L+k}^{R-L+1}-1$，使用lucas直接求解即可。

时间复杂度为$O(Tlo{g}_p^N(p+logp))$。

#include <iostream>

using namespace std;

typedef long long LL;

const int p = 1e6 + 3;

int qmi(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = (LL) res * a % p;
        a = (LL) a * a % p;
        b >>= 1;
    }
    return res;
}
int C(int a, int b) {
    int up = 1, down = 1;
    for (int i = a, j = 1; j <= b; ++ j, -- i) {
        up = (LL) up * i % p;
        down = (LL) down * j % p;
    }
    return (LL) up * qmi(down, p - 2) % p;  //逆元
}
int Lucas(int a, int b) {
    if (a < p && b < p) return C(a, b);
    return (LL)C(a % p, b % p) * Lucas(a / p, b / p) % p;
}
int main() {
    int T;
    cin >> T;
    while (T -- ) {
        int n, l, r;
        cin >> n >> l >> r;
        cout << (Lucas(r - l + n + 1, r - l + 1) - 1 + p) % p << endl;
    }
    return 0;
}

网络

某城市的街道呈网格状，左下角坐标为 $A(0,0)$，右上角坐标为 $B(n,m)$，其中 $n\ge m$。

现在从 $A(0,0)$ 点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点 $(x,y)$ 都要满足 $x\ge y$，请问在这些前提下，到达 $B(n,m)$ 有多少种走法。

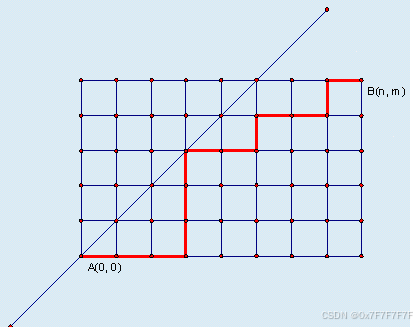
输入格式

仅有一行，包含两个整数 $n$ 和 $m$，表示城市街区的规模。

输出格式

输出一个整数，表示不同的方案总数。

数据范围
$1\le m\le n\le 5000$

输入样例：

6 6

输出样例：

132

依据卡特兰数的推导，找出$(n,m)$关于$y=x+1$的对称点$(m-1,n+1)$，每一条非法路径都对应一条$(0,0)$到$(m-1,n+1)$的路径，因此合法路径=总路径数-非法路径，即$C_{n+m}^n-C_{n+m}^{m-1}$。

#include <iostream>
using namespace std;
const int N = 10010;
int primes[N], cnt;
bool st[N];
int a[N], b[N];
int n, m;
void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[primes[j] * i] = 1;
            if (i % primes[j] == 0) break;
        }
    }
}
int get(int n, int p)
{
    int s = 0;
    while (n) s += n / p, n /= p; 
    return s;
}
void mul(int r[], int &len, int p)
{
    int t = 0;
    for (int i = 0; i < len; i ++ )
    {
        t += r[i] * p;
        r[i] = t % 10;
        t /= 10;
    }
    while (t)
    {
        r[len ++ ] = t % 10;
        t /= 10;
    }
}
int C(int a, int b, int r[])
{
    int len = 1;
    r[0] = 1;
    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        int s = get(a, p) - get(b, p) - get(a - b, p);
        while (s -- ) mul(r, len, p);
    }
    return len;
}
void sub(int a[], int al, int b[], int bl)
{
    for (int i = 0, t = 0; i < al; i ++ )
    {
        a[i] -= t + b[i];
        if (a[i] < 0) a[i] += 10, t = 1;
        else t = 0;
    }
}
int main()
{
    cin >> n >> m;
    init(N - 1);
    int al = C(n + m, n, a);
    int bl = C(n + m, m - 1, b);
    sub(a, al, b, bl);
    int k = al - 1;
    while (!a[k]) k -- ;
    while (k >= 0) cout << a[k -- ];
    return 0;
}

有趣的数列

我们称一个长度为 $2n$ 的数列是有趣的，当且仅当该数列满足以下三个条件：

• 它是从 $1\sim 2n$ 共 $2n$ 个整数的一个排列 {an}n=12n\{a_n\}_{n=1}^{2n}{an​}n=12n​；

• 所有的奇数项满足 $a_1<a_3<\cdots <a_{2n-1}$，所有的偶数项满足 $a_2<a_4<\cdots <a_{2n}$；

• 任意相邻的两项 $a_{2i-1}$ 与 $a_{2i}$ 满足：$a_{2i-1}<a_{2i}$。

对于给定的 $n$，请求出有多少个不同的长度为 $2n$ 的有趣的数列。
因为最后的答案可能很大，所以只要求输出答案对 $p$ 取模。

输入格式

一行两个正整数 $n,p$

输出格式

输出一行一个整数表示答案。

输入输出样例 #1

输入 #1

3 10

输出 #1

5

说明/提示

【数据范围】
对于 $50\%$ 的数据，$1\le n\le 1000$；
对于 $100\%$ 的数据，$1\le n\le 10^6$，$1\le p\le 10^9$。

【样例解释】
对应的5个有趣的数列分别为（1,2,3,4,5,6），（1,2,3,5,4,6），（1,3,2,4,5,6），（1,3,2,5,4,6），（1,4,2,5,3,6）。

分析一道题是不是卡特兰数的方法有两种
1.从递推式的角度来看，如果$f[n]=f[1]\ast f[n-1]+f[2]\ast f[n-2]$… 那么就是卡特兰数，比如求二叉树的个数
2.挖掘一种性质：任意前缀中，某种东西一定不能少于等于另一种东西。

从$1$到$2n$把每个数依次分给每个奇数堆和偶数堆，分析可得，在任意时候奇数堆的数量都要>=偶数堆的数量，因此本题是标准的catlan数模型。另外由于$p$不一定是质数，所以不能用逆元的方法求组合数，要使用分解质因数结合快速幂的方法。
时间复杂度为$O(n+n/ln(n)\ast (lo{g}_p^n+loglogn))$，其中$n$是求素数的时间花费，$n/ln(n)$是分解质因数的过程中需要枚举的质数数量，$lo{g}_p^n$为求质数$p$数量的时间花费，$loglogn$是快速幂的时间花费,时间复杂度接近于$O(n)$。

#include <iostream>
using namespace std;
typedef long long ll;
const int N = 2000010;
int primes[N], cnt;
bool st[N];
int n, p;
void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[primes[j] * i] = 1;
            if (i % primes[j] == 0) break;
        }
    }
}
int get(int n, int p)
{
    int s = 0;
    while (n) s += n / p, n /= p;
    return s;
}
int qmi(int a, int k)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = res * a % p;
        k >>= 1;
        a = a * a % p;
    }
    return res;
}
int C(int a, int b)
{
    int res = 1;
    for (int i = 0; i < cnt; i ++ )
    {
        int prime = primes[i];
        int s = get(a, prime) - get(b, prime) - get(a - b, prime);
        res = (ll) res * qmi(prime, s) % p;
    }
    return res;
}
int main()
{
    cin >> n >> p;
    init(N - 1);
    cout << (C(n * 2, n) - C(n * 2, n - 1) + p) % p;
    return 0;
}