【DL学习笔记11】《深度学习进阶——自然语言处理》—— ch04：word2vec的高速化

已于 2022-07-12 21:44:30 修改
阅读量404 收藏 2
点赞数 2
分类专栏： DL学习笔记 文章标签： python 人工智能 word2vec 自然语言处理
于 2022-07-12 21:36:05 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_71268863/article/details/125752536
版权

目录

1. 改进一：Embedding层

2. 改进二：Negative Sampling（负采样）

多分类到二分类的实现

负采样

采样方法

负采样的实现

3. 改进版word2vec的学习

CBOW模型的实现

CBOW模型的学习代码

CBOW模型的评价

4. word2vec相关的其他话题

应用例

单词向量的评价方法

CBOW是一个简单的2层神经网络，但随着语料库中处理的词汇量的增加，计算量也随之增加，因此本章将重点放在word2vec的加速上。总体而言有两点改进：引入Embedding层和Negative Sampling损失函数

  • 假设词汇量有100万个，CBOW模型的中间层有100个，以下两个地方的计算会出现瓶颈
    • 输入层的one-hot表示和权重矩阵W_{in} 的乘积（Embedding层解决）
    • 中间层和权重矩阵W_{out} 的乘积以及Softmax层的计算（Negative Sampling损失函数解决）

1. 改进一：Embedding层

  • 其实one-hot表示与权重矩阵的乘积，无非是将矩阵中某个特定的行取出来，因此我们用Embedding层实现从权重参数中抽取“单词ID对应行”的行为
  • 实现：
class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None  # 保存需要提取的行的索引

    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

    def backward(self, dout):
        dW, = self.grads
        dW[...] = 0  # 保持dw的形状不变，将元素设为0
        dW[self.idx] = dout  # 不太好的方式
        return None
  • backward中创建了和权重大小相同的矩阵dW，并将梯度写入了dW对应的行。但是我们想做的事情是更新权重W，所以只需要把要更新的行号(idx)及其对应的梯度(dout)保存下来。但是这里是为了兼容优化器类Optimizer
  • 问题：如果idx的元素出现重复时，比如[0, 2, 0, 4]，这时简单的将值写入dW中idx指定的位置，某个值就会被覆盖掉
  • 解决：进行“加法”而不是“写入”。个人认为idx中元素重复出现，说明上下文中这个单词出现多次，对目标词影响是累积的
# 改进的backward
def backward(self, dout):
        dW, = self.grads
        dW[...] = 0
        np.add.at(dW, self.idx, dout)  # 将dout加到dW指定的idx的行上
        return None

2. 改进二：Negative Sampling（负采样）

  • 中间层之后的计算问题：
    • 中间层的神经元和权重矩阵的乘积
    • Softmax层的计算
  • 从多分类到二分类
    • 负采样的关键思想在于用二分类(binary classification)拟合多分类(multiclass classification)
    • 二分类处理的是答案为“Yes/No”的问题
    • 我们考虑，能不能把从100万个单词中选择1个正确单词的任务处理成当上下文是you和goodbye时，目标词是say吗？这时输出层只需要一个神经元即可
    • 因此要计算中间层和输出侧的权重矩阵的乘积，只要提取say对应的列计算内积即可
  • sigmoid函数和交叉熵误差
    • 多分类情况下，输出层使用softmax函数，二分类情况下，输出层使用sigmoid函数，损失函数都用交叉熵误差

多分类到二分类的实现

  • 改进前：

  • 改进后

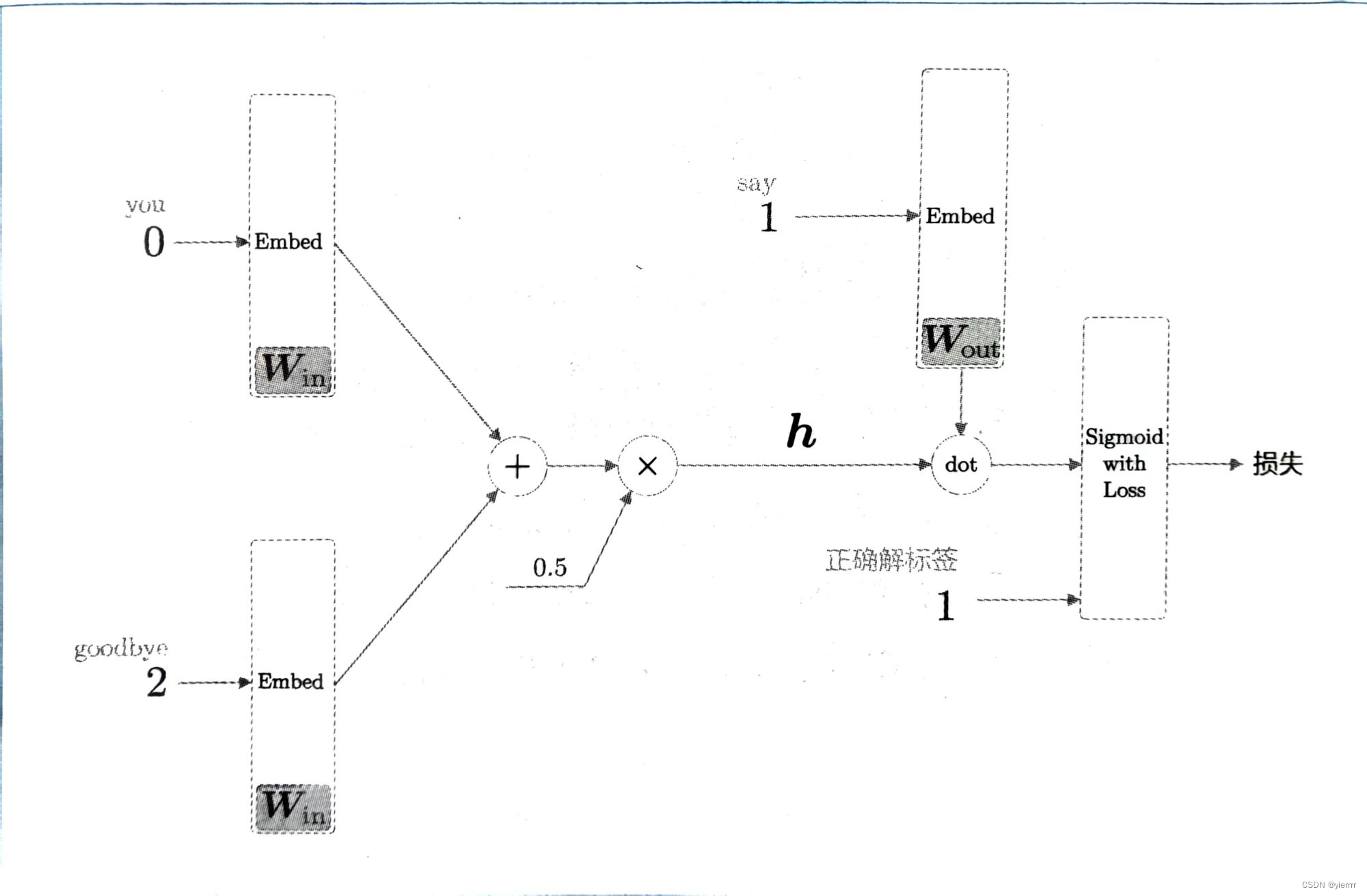
  • 输入的正确解标签是1，意味着答案是yes，0意味着答案是no

  • 引入Embedding Dot层，将后半部分进一步简化，将Embed层和dot运算(内积)合并起来运算

class EmbeddingDot:
    def __init__(self, W):
        self.embed = Embedding(W)
        self.params = self.embed.params
        self.grads = self.embed.grads
        self.cache = None  # 保存正向传播时的计算结果

    def forward(self, h, idx):  # 接收中间层的神经元和单词ID的NumPy数组(mini-batch)
        target_W = self.embed.forward(idx)
        out = np.sum(target_W * h, axis=1)  # 计算内积

        self.cache = (h, target_W)
        return out

    def backward(self, dout):
        h, target_W = self.cache
        dout = dout.reshape(dout.shape[0], 1)

        dtarget_W = dout * h
        self.embed.backward(dtarget_W)
        dh = dout * target_W
        return dh

负采样

  • 目前我们仅学习了正例（正确答案），还不确定负例（错误答案）会有怎样的结果。
  • 我们期望对于正例，Sigmoid层输出接近1，对于负例，接近0
  • 但我们显然不能以所有的负例作为对象进行学习，因为学习词汇量将暴增，与我们为了解决词汇量增加的问题相悖。为此，作为一种近似的方法，我们将选择若干个负例
  • 负采样方法：既可以求将正例作为目标词时的损失，也可以采样若干个负例求损失，然后将正例和采样出来的负例的损失加起来，作为最终损失

采样方法

  • 基于语料库的统计数据进行采样，让常出现的单词更容易被抽到
  • 基于语料库中单词使用频率的采样方法会先计算语料库中各个单词的出现次数，并将其表示为“概率分布”
  • 考虑到计算的复杂度，有必要将负例限定在较小范围（5个或10个），且选择高频单词会获得更好的结果，因为稀有单词基本上不会出现，重要性较低
  • 对基于概率分布进行采用的理解（对random.choice()的理解）
>>>import numpy as np

# 从0到9的数字里随机选择一个数字
>>>np.random.choice(10)
1
>>>np.random.choice(10)
5

# 从words列表中随机选择一个元素
>>>words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
>>>np.random.choice(words)
'hello'

# 有放回的采样5次
>>>np.random.choice(words, size=5)
array(['you', 'hello', '.', 'say', 'you'], dtype='<U7')
# 无放回的采样5次
>>>np.random.choice(words, size=5, replace=False)
array(['I', 'say', 'hello', 'goodbye', '.'], dtype='<U7')

# 基于概率分布进行采样
>>>p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
>>>np.random.choice(words, p=p)
'you'
  • word2vec中提出的负采样增加了一个步骤
    • 对原来的概率分布取0.75次方：{P}'=\frac{P(w_i)^{0.75}}{\sum_j^n P(w_j)^{0.75}}
    • 这是为了防止低频单词被忽略，通过取0.75次方，低频单词的概率将稍微变高
  • 总结：负采样从语料库生成单词的概率分布，在取其0.75次方之后，再使用之前的np.random.choice()对负例进行采样
  • 实现：
class UnigramSampler:
    def __init__(self, corpus, power, sample_size):
				"""

        @param corpus: 单词ID列表
        @param power: 对概率分布取的次方值(默认为0.75)
        @param sample_size: 负例的采样个数
        """
        self.sample_size = sample_size
        self.vocab_size = None
        self.word_p = None

        counts = collections.Counter()
        for word_id in corpus:
            counts[word_id] += 1

        vocab_size = len(counts)
        self.vocab_size = vocab_size

        self.word_p = np.zeros(vocab_size)
        for i in range(vocab_size):
            self.word_p[i] = counts[i]

        self.word_p = np.power(self.word_p, power)
        self.word_p /= np.sum(self.word_p)

    def get_negative_sample(self, target):
				"""以target指定的单词ID为正例，对其他的单词ID进行采样

        @param target: 指定的正例的单词ID
        @return: 负例的单词ID列表
        """
        batch_size = target.shape[0]

        if not GPU:
            negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)

            for i in range(batch_size):
                p = self.word_p.copy()
                target_idx = target[i]
                p[target_idx] = 0
                p /= p.sum()
                negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)
        else:
            # 在用GPU(cupy）计算时，优先速度
            # 有时目标词存在于负例中
            negative_sample = np.random.choice(self.vocab_size, size=(batch_size, self.sample_size),
                                               replace=True, p=self.word_p)

        return negative_sample

负采样的实现

class NegativeSamplingLoss:
    def __init__(self, W, corpus, power=0.75, sample_size=5):
        """

        @param W: 输出侧权重W
        @param corpus: 语料库(单词ID列表)
        @param power: 概率分布的次方值
        @param sample_size: 负例的采样数
        """
        self.sample_size = sample_size
        # 生成UnigramSampler类并用成员变量sampler保存
        self.sampler = UnigramSampler(corpus, power, sample_size)
        # 用列表保存必要的层，sample_size个负例用的层和一个正例用的层
        self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
        self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]

        self.params, self.grads = [], []
        for layer in self.embed_dot_layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, h, target):
        # 接收中间层的神经元和正例目标target
        batch_size = target[0]
        # 采样负例
        negative_sample = self.sampler.get_negative_sample(target)

        # 正例的正向传播
        score = self.embed_dot_layers[0].forward(h, target)  # 得分
				# 正例的正确解标签，值为1，长度为正例目标的个数
        correct_label = np.ones(batch_size, dtype=np.int32)
        loss = self.loss_layers[0].forward(score, correct_label)  # 损失

        # 负例的正向传播
        negative_label = np.zeros(batch_size, dtype=np.int32)  # 负例的正确解标签，值为0
        for i in range(self.sample_size):
            negative_target = negative_sample[:, i]  # 取出负例目标，以批大小为单位
            score = self.embed_dot_layers[1 + i].forward(h, negative_target)  # 得分
						# 累加正例目标和各个负例目标的损失
            loss += self.loss_layers[1 + i].forward(score, negative_label)  

        return loss

    def backward(self, dout=1):
        dh = 0
        for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
            dscore = l0.backward(dout)
            dh += l1.backward(dscore)

        return dh

3. 改进版word2vec的学习

CBOW模型的实现

  • 使用Embedding层和Negative Sampling Loss层，并将上下文部分扩展为可以处理任意的窗口大小
  • 初始化权重：改进前的输入侧权重和输出侧权重形状不同，输出侧的权重在列方向上排列单词向量。改进后的形状相同，都在行方向上排列单词向量
  • forward中的参数是单词ID形式而不是原来的one-hot形式，因为Embedding层中需要的参数是需要提取的单词的索引，也就是单词ID
class CBOW:
    def __init__(self, vocab_size, hidden_size, window_size, corpus):
        """
        @param vocab_size: 词汇量
        @param hidden_size: 中间层的神经元个数
        @param window_size: 上下文的大小
        @param corpus: 语料库(单词ID列表)
        """
        V, H = vocab_size, hidden_size

        # 初始化权重
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(V, H).astype('f')

        # 生成层
        self.in_layers = []
        for i in range(2 * window_size):
            layer = Embedding(W_in)  # 使用Embedding层
            self.in_layers.append(layer)
        self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
        layers = self.in_layers + [self.ns_loss]

        # 将所有的权重和梯度整理到列表中
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 将单词的分布式表示设置为成员变量
        self.word_vecs = W_in

		# 这里的上下文和目标词但是单词ID形式，不同于之前用的one-hot表示
    def forward(self, contexts, target):
        h = 0
        for i, layer in enumerate(self.in_layers):
            h += layer.forward(contexts[:, i])  # 遍历上下文
        h *= 1 / len(self.in_layers)
        loss = self.ns_loss.forward(h, target)
        return loss

    def backward(self, dout=1):
        dout = self.ns_loss.backward(dout)
        dout *= 1 / len(self.in_layers)
        for layer in self.in_layers:
            layer.backward(dout)
        return None

CBOW模型的学习代码

# 设定超参数
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10

# 读入数据
print("读入数据")
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)

contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
    contexts, target = to_gpu(contexts), to_gpu(target)

# 生成模型等
print("生成模型")
model = CBOW(vocab_size, hidden_size, window_size, corpus)
# model = SkipGram(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)

# 开始学习
print("开始学习")
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()

# 保存必要数据，以便后续使用
word_vecs = model.word_vecs
if config.GPU:
    word_vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl'  # or 'skipgram_params.pkl'
with open(pkl_file, 'wb') as f:
    pickle.dump(params, f, -1)

 

CBOW模型的评价

  • 我们使用第2章中实现的most_similar()函数，显示几个单词的最接近的单词
pkl_file = 'cbow_params.pkl'
# pkl_file = 'skipgram_params.pkl'

with open(pkl_file, 'rb') as f:
    params = pickle.load(f)
    word_vecs = params['word_vecs']
    word_to_id = params['word_to_id']
    id_to_word = params['id_to_word']

# most similar task
querys = ['you', 'year', 'car']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

# analogy task
print('-'*50)
analogy('king', 'man', 'queen',  word_to_id, id_to_word, word_vecs)
analogy('take', 'took', 'go',  word_to_id, id_to_word, word_vecs)
analogy('car', 'cars', 'child',  word_to_id, id_to_word, word_vecs)

"""  输出
[query] you
 we: 0.736328125
 i: 0.71240234375
 anybody: 0.59912109375
 your: 0.595703125
 they: 0.58642578125
[query] year
 month: 0.8642578125
 week: 0.78857421875
 summer: 0.76953125
 spring: 0.75244140625
 decade: 0.6728515625
[query] car
 truck: 0.62646484375
 luxury: 0.619140625
 window: 0.5947265625
 auto: 0.5927734375
 merkur: 0.5888671875
--------------------------------------------------
[analogy] king:man = queen:?
 a.m: 5.51953125
 carolinas: 5.05078125
 woman: 4.80859375
 wife: 4.73828125
 toxin: 4.6328125
[analogy] take:took = go:?
 were: 4.578125
 're: 4.4765625
 went: 4.265625
 came: 4.22265625
 eurodollars: 4.06640625
[analogy] car:cars = child:?
 a.m: 6.24609375
 rape: 5.63671875
 children: 5.39453125
 women: 5.0859375
 adults: 5.02734375
"""
  • 通过most_similar()函数，我们可以得到和目标词的近似单词
  • 此外，由word2vec获得的单词的分布式表示，不仅可以将近似单词聚拢在一起，还可以捕获更复杂的模式，其中一个具有代表性的例子是因“king - man + woman = queen”而出名的类推问题。
  • 更准确地说，使用word2vec的单词的分布式表示，可以通过向量的加减法来解决类推问题：在单词向量空间上寻找尽可能使“man→woman”向量和“king→?”向量接近的单词
  • analogy()：实现类推
def analogy(a, b, c, word_to_id, id_to_word, word_matrix, top=5, answer=None):
    for word in (a, b, c):
        if word not in word_to_id:
            print('%s is not found' % word)
            return

    print('\\n[analogy] ' + a + ':' + b + ' = ' + c + ':?')
    a_vec, b_vec, c_vec = word_matrix[word_to_id[a]], word_matrix[word_to_id[b]], word_matrix[word_to_id[c]]
    query_vec = b_vec - a_vec + c_vec
    query_vec = normalize(query_vec)

    similarity = np.dot(word_matrix, query_vec)

    if answer is not None:
        print("==>" + answer + ":" + str(np.dot(word_matrix[word_to_id[answer]], query_vec)))

    count = 0
    for i in (-1 * similarity).argsort():
        if np.isnan(similarity[i]):
            continue
        if id_to_word[i] in (a, b, c):
            continue
        print(' {0}: {1}'.format(id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
  • 像这样，使用word2vec获得的单词的分布式表示，可以通过向量的加减法求解类推问题，不仅限于单词的含义，也捕获到了语法中的模式

4. word2vec相关的其他话题

应用例

  • 在NLP领域，单词的分布式表示之所以重要，原因在于迁移学习(transfer learning)，是指在某个领域学到的知识可以被应用于其它领域
  • 在解决NLP问题时，一般是现在大规模语料库上学习，然后将学习好的分布式表示应用于某个单独的任务。比如在文本分类、文本聚类、情感分析等NLP问题中，第一步的单词量化工作就可以使用学习好的单词的分布式表示
  • 邮件的自动分类系统（情感分析）的例子
    1. 收集数据（邮件），并人工对邮件进行标注，打上表示3类情感的标签（positive/ neutral/ negative）
    2. 用学习好的word2vec将邮件转化为向量
    3. 将向量化的邮件及其情感标签输入某个情感分类系统进行学习
  • 总的来说，我们可以基于单词的分布式表示将NLP问题转化为向量，这样就可以利用常规的机器学习方法来解决问题

单词向量的评价方法

  • 我们最终想要的是一个高精度的系统，但必须考虑的是，这个系统是由多个子系统组成的，单词的分布式表示就是一个子系统，因此我们要先进行单词的分布式表示的学习，然后再进行另一个机器学习系统的学习，在进行两个阶段的学习之后，才能进行评价，这是非常耗时的
  • 因此我们要单独进行单词向量的评价，常有指标有”相似度“和”类推问题“
  • 相似度：通常使用人工创建的单词相似度评价集来评估，比较人给出的0-10的分数和word2vec给出的余弦相似度，考察它们之间的相关性
  • 类推问题：基于诸如”king : queen = man : ?“这样的类推问题，根据正确率测量优劣
  • 注意：单词的分布式表示的影响，取决于待处理问题的具体情况，不能保证类推问题的评价高，目标应用的结果就一定好
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值