1.用筛选法求100之内的素数
#include<stdio.h>
int main()
{
int i, j;
int a[100];
for (i = 0; i < 100; i++) //初始化数组
a[i] = i + 1;
a[0] = 0;
for (i = 1; i < 100; i++) //因为1是素数,直接从2开始遍历
{
if (a[i] == 0) //如果a[i] = 0,跳过本次循环
continue;
// 如果能够整除则一定不是素数,该位置数据用0填充
for (j = i + 1; j < 100; j++)
{
if (a[j] % a[i] == 0) //把不是素数的元素都赋值为0
/*if (a[i] != 0 &&a[j] !=0 && a[j] % a[i] == 0)*/
a[j] = 0;
}
}
printf("用筛选法求出100以内的素数为:\n");
for (i = 0; i < 100; i++)
{
if (a[i] != 0) //数组中不为0的数即为素数
printf("%d\n", a[i]);
}
return 0;
}
运行结果:


代码逻辑:
1.如何处理不是素数的元素
2.循环时的判断条件
一.初始化数组
int i, j;
int a[100];
for (i = 0; i < 100; i++)
a[i] = i + 1; //公差为1的等差数列
二.遍历循环,将不是素数的元素赋值为0
a[1] = 0;
for (i = 1; i < 100; i++) //因为1是素数,直接从2开始遍历
{
if (a[i] == 0) //如果a[i] = 0,跳过本次循环
continue;
// 如果能够整除则一定不是素数,该位置数据用0填充
for (j = i + 1; j < 100; j++)
{
if (a[j] % a[i] == 0) //把不是素数的元素都赋值为0
a[j] = 0;
}
}
if (a[i] != 0 && a[j] % a[i] == 0) //省略continue的写法
跳过之前已经被赋值为0的非素数,也就是a[i] = 0的元素
三.输出不为0的素数
for (i = 0; i < 100; i++)
{
if (a[i] != 0) //数组中不为0的数即为素数
printf("%d\n", a[i]);
}
注:
1.筛选法
基本概念:筛选法主要用于寻找一定范围内的质数(素数)。其基本原理是通过连续筛除一个质数的所有倍数来找出所有质数,逐步排除掉非质数,最终留下质数。
操作步骤:
-
将N个自然数按次序排列,首先划去1(因为1既不是质数也不是合数)。
-
保留2,并划去所有2的倍数(除了2本身)。
-
接下来,保留3(因为它是第一个未被划去的数,且是质数),并划去所有3的倍数。
-
重复上述步骤,每次保留下一个未被划去的数(即下一个质数),并划去该质数的所有倍数。
-
如此继续,直到遍历完所有数,最终留下的就是不超过N的全部质数。
2.关于为什么要验证a[i]是否等于0的问题
因为第二个for(j)循环遍历了能除以当前质数的数,并将它们赋值为0.在第二个质数遍历时,直接跳过已经赋值为0的数,因为这个被跳过的数可能是两个质数的公倍数。
if (a[i] != 0 &&a[j] !=0 && a[j] % a[i] == 0)
也可不用continue语句,直接写进条件判断里
2. 用选择法对10个整数排序
2.1初始化一个数组
int main()
{
int i = 0;
int arr[10] = { 0 };
for (i = 0; i < 9; i++)
{
arr[i + 1] = arr[i] + 1; //9=8+1
printf("%d\n", arr[i]);
}
return 0;
}
运行结果:

冒泡排序:
#include <stdio.h>
int main()
{
int arr[10] = {10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
int i = 0;
int j = 0;
int temp = 0;
for (i = 0; i < 9; i++) //确定冒泡排序的趟数
{
//一趟冒泡排序的过程
for (j = 0; j < 9 - i; j++) //确定一趟冒泡排序比较的对数
{
if (arr[j] > arr[j + 1]) //如果前一项大于后一项,交换次序
{
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
printf("一共比较了%d次\n", n);
for (i = 0; i < 10; i++)
{
printf("%d\n", arr[i]);
}
return 0;
}运行结果:

标准代码:
#include<stdio.h>
int main()
{
int arr[10] = { 2,8,3,9,5,7,1,4,0,6 };
int i, j, temp;
//通过用测量的数组所占字节的大小除以单个元素所占的大小,来确定数组元素的个数
int size = sizeof(arr) / sizeof(arr[0]);
for (i = 0; i < size - 1; i++)
{
int minIndex = i; // 假定当前元素为最小值
for (j = i + 1; j < size; j++)
{
if (arr[j] < arr[minIndex]) // 搜索更小的元素
{
minIndex = j; // 更新最小值的索引
}
}
// 若最小值索引并非当前外层循环的元素索引,则执行交换
if (minIndex != i)
{
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
// 打印排序后的数组
for (i = 0; i < size; i++)
{
printf("%d\n", arr[i]);
}
return 0;
}运行结果:

代码逻辑:
一.用sizeof函数求出数组的元素个数用以限定循环范围
二.内层循环先设定了一个最小值 int minIndex = i;,循环比较 j = minIndex;,如果索引不同,那么用判断条件更换索引 if (minIndex != i)...
1.求出数组的元素个数,后续的循环次数都可以以此为界限
通过用测量的数组所占字节的大小除以单个元素所占的大小,来确定数组元素的个数
int size = sizeof(arr) / sizeof(arr[0]);
2.外层循环
for (i = 0; i < size - 1; i++)
3.内层循环
int min = arr[i]; // 假定当前元素为最小值
for (j = i + 1; j < size; j++)
{
if (arr[j] < arr[min]) // 搜索更小的元素
{
min = j; // 更新最小值的索引
}
// 若最小值下标并非当前外层循环的元素下标,则执行交换
if (min != i)
{
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
注:
- 初始状态:从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置。
- 后续过程:再从剩余的元素中选出最小(或最大)的一个,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。
3. 求一个3*3的整形矩阵对角线元素之和
3.1 错误例子(降维解决不具有普遍性)
#include<stdio.h>
int main()
{
int arr[9] = { 1,2,3,4,5,6,7,8,9 };
int i = 0;
int sum_left = 0;
int sum_right = 0;
for (i = 0; i < 9; i = i + 4)
{
sum_left += arr[i];
}
printf("3*3矩阵的主对角线之和为:%d\n", sum_left);
for (i = 2; i < 8; i = i + 2)
{
sum_right += arr[i];
}
printf("3*3矩阵的副对角线之和为:%d\n", sum_right);
return 0;
}运行结果:

标准代码:
#include<stdio.h>
int main()
{
int arr[3][3] = { {1,2,3},{ 4,5,6 },{ 7,8,9 } }; //定义一个二维数组
int i = 0;
int sum_left = 0;
int sum_right = 0;
for (i = 0; i < 3; ++i)
{
sum_right += arr[i][i]; //主对角线,元素行等于列
}
printf("3*3矩阵的主对角线之和为:%d\n", sum_right);
for (i = 0, j = 2; i < 3; ++i, j--) //副对角线(行++、列--)求和
{
sum_left += arr[i][j];
}
printf("3*3矩阵的副对角线之和为:%d\n", sum_left);
return 0;
}
代码逻辑:
利用矩阵中行于列的位置关系设定限制条件进行求和
注:
1.错误例子利用了矩阵中对角线元素之间一维空间的位置关系(等差数列),因此不能推广到一般形式
具体情况:
在进行矩阵的初始化时,利用位置关系定义成一维数组
int arr[9] = { 1,2,3,4,5,6,7,8,9 };
主对角线:0 + 4 + 8 副对角线:2 + 4 + 6
for (i = 0; i < 9; i++) for (j = 0; i < 8; j++)
sum += arr[i] sum += arr[j]
因此在4*4矩阵中又要重新设定循环条件,不具有普遍性,也不符合题意
2.循环条件的设定需要考虑到数组中的元素是从0开始的,因此应该注意要从第0行第0列考虑限制条件
4. 有一个已经排好序的数组,要求输入一个数后,按原来顺序的规律将它插入数组中
#include<stdio.h>
int main()
{
int arr[5] = { 0,1,2,3,4 };
int newarr[6] = { 0 };
int i = 0;
int j = 3;
for (i = 0; i < 5; i++)
{
//strcpy 函数用于复制字符串(字符数组),而不是用于复制整数数组
strcpy(newarr[i], arr[i]);
if (newarr[i] <= j < newarr[i + 1]) //数组元素递增,且把j插入偏后的位置
{
newarr[i + 1] = j;
newarr[i + 2] = newarr[i + 1];
}
}
for (i = 0; i < 6; i++)
{
printf("%d\n", arr[i]);
}
return 0;
}注:
strcpy 函数用于复制字符串(字符数组),而不是用于复制整数数组
strcpy(newarr[6], arr[5]);
一旦数组被定义,其大小(即元素个数)就是固定的,不能在运行时改变。数组的大小是在编译时确定的,并且数组在内存中是连续存储的,因此改变数组大小通常意味着需要分配一个新的数组并可能复制旧数组的数据到新数组中。
4.1覆盖前一个数组
#include<stdio.h>
int main()
{
int arr[5] = { 0,1,2,3,4 };
int newarr[6] = { 0 };
int i = 0;
for (i = 0; i < 5; i++)
{
newarr[i] = arr[i];
}
for (i = 0; i < 5; i++)
{
printf("%d\n", newarr[i]);
}
return 0;
}运行结果:
![]()
4.2标准代码:
#include<stdio.h>
int main()
{
int a[6] = { 0,1,3,3,4 };
int i,j,num,temp1,temp2;
printf("请输入一个整数:"); //插入一个元素num
scanf("%d", &num);
if (num > a[4]) //如果num大于最大值,直接赋值
a[5] = num;
else
{
for (i = 0; i < 5; i++)
{
if (a[i] > num)
{
temp1 = a[i];
a[i] = num;
for (j = i + 1; j < 6; j++)
{
temp2 = a[j]; //把后一项的值赋给temp2
a[j] = temp1; //把temp1也就是a[i]的值往后推一位
temp1 = temp2; //在循环末尾,把后一项的值赋给前一项
}
break; //条件满足时,跳出内层循环
}
}
}
for (i = 0; i < 6; i++)
{
printf("%d ", a[i]);
}
return 0;
}代码逻辑:
一.先把num后一项的元素a[i]赋值给temp1,然后把num填入a[i]中。通过j = i +1,把后一项的值赋给temp2,然后把temp1的值赋给后一项的a[j](a[i+1]),最后把temp2的值赋给temp1达到插入的目的。
具体情况:
int a[6] = { 0,1,3,3,4 };
当 num = 2时,temp1 = 3,a[2] = 2;
进入循环 for (j = i + 1; j < 6; j++)
j = i + 1 i = 3时 i = 4时
temp2 = a[j]; temp2 = a[3] = 3 temp2 = a[4]= 4
a[j] = temp1; a[3] = temp1 = 3 a[4] = temp1 = 4
temp1 = temp2; temp1 = temp2 = 2 temp1= temp2 = 2
1. 如果num大于最大值,直接赋值
if (num > a[4])
a[5] = num;
2.否则进入判断循环
else
{
for (i = 0; i < 5; i++)
{
3.通过两个变量temp1、temp2把元素循环赋值
if (a[i] > num)
{
temp1 = a[i];
a[i] = num;
for (j = i + 1; j < 6; j++)
{
temp2 = a[j]; //把后一项的值赋给temp2
a[j] = temp1; //把temp1也就是a[i]的值往后推一位
temp1 = temp2; //在循环末尾,把后一项的值赋给前一项
}
4.循环进行结束时,直接跳出循环
break; //条件满足时,跳出内层循环
}
}
}
5.将一个数组中的值按逆序重新存放。例如:原来顺序为8,6,5,4,1。 要求改为1,4,5,6,8。
5.1错误例子
#include<stdio.h>
int main()
{
int a[5] = { 8,6,5,4,1 };
int i = 0;
int end = 4;
for (i = 0; i < 5; i++)
{
a[i] = a[end];
end--;
}
for (i = 0; i < 5; i++)
{
printf("%d", a[i]);
}
return 0;
}运行结果:

代码逻辑:
一.没有中间变量的储存交换、导致循环遍历会对称,一个元素的值会赋给两个元素
二.循环次数应该是两次也就是 i < 2
int end = 4;
for (i = 0; i < 5; i++)
{
a[i] = a[end];
end--;
}
具体情况:
a[0] = a[4] = 1
a[1] = a[3] = 4
a[2] = a[2] = 5
a[3] = a[1] = 4
a[4] = a[0] = 1
标准代码:
#include<stdio.h>
int main()
{
int a[5] = { 8,6,5,4,1 };
int i = 0;
int temp = 0;
int end = 4; //标记结尾元素下标
for (i = 0; i < 2; i++) // 只需要遍历到数组的一半
{
temp = a[i]; //用中间变量储存交换的值
a[i] = a[end - i];
a[end - i] = temp;
}
for (i = 0; i < 5; i++)
{
printf("%d ", a[i]);
}
return 0;
}运行结果:

6.输出以下的杨辉三角(要求输出10行)

#include<stdio.h>
int main()
{
int a[10][10] = {0};
int i = 0, j = 0;
for (i = 0; i < 10; i++) //循环10次
{
for (j = 0; j < i + 1; j++)
{
if (j == 0 || i == j) //第一列和对角线元素统一赋值为1
a[i][j] = 1;
else
a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
}
}
for (i = 0; i < 10; i++)
{
for (j = 0; j < i + 1; j++)
{
printf("4%d ", a[i][j]);
}
printf("\n"); //每次打印完一行,打印一个换行符
}
return 0;
}运行结果:
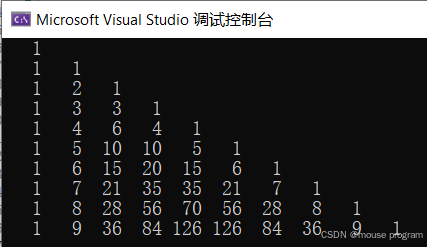
代码逻辑:
一.定义一个二维数组。通过设置内外循环条件,使得数组能够循环10行10列
二.第一列和对角线元素统一赋值为1,其余元素值的规律均为该元素正上方的值和正上方左侧值之和(例:a[3][2] = a[2][2] + a[2][1]))
1. 内外层循环的设定
i = 0时 j = 0,i = 1时,j = 0,j = 1
for (i = 0; i < 10; i++) //循环10次
{
for (j = 0; j < i+1; j++)
{
2.特殊位置和一般位置元素的赋值
if (j == 0 || i == j) //第一列和对角线元素统一赋值为1
a[i][j] = 1;
else
a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
}
}
7. 输出"魔方阵"。所谓魔方阵是指这样的方阵,它的每一行、每一列和对角线之和均相等。
附:
输入一个1~15之间的奇数n
输出1~n*n的自然数所构成的魔方阵(错误)
这本身就是一个错误的要求,因为有些偶数阶(例如2阶)的魔方阵根本不存在,而且从后面的代码来看,题目根本没有输出偶数阶魔方阵的意图。
7.1错误例子
#include<stdio.h>
int main()
{
int a[15][15] = { 0 };
int i, j, sum_row = 0, sum_column = 0, sum_right = 0, sum_left = 0;
for (i = 0; i < 15; i++)
{
for (j = 0; j < 15; j++)
{
if (i == i || j == j || i == j)
sum_row += a[i][j];
sum_column += a[i][j];
sum_right = a[i][j];
for (i = 0; i < 15; i++)
{
for (j = 0; j < 15 - i; j++)
sum_left += a[i][j];
}
}
}
while (sum_row == sum_column == sum_right == sum_left)
{
for (i = 0; i < 15; i++)
{
for (j = 0; j < 15; j++)
{
printf("%d", a[i][j]);
}
printf("\n");
}
}
return 0;
}7.2标准代码
#include <stdio.h>
int main()
{
int a[15][15] = { 0 };
int n, i, j, k;
//输入奇数n
while (1)
{
printf("请输入n(1~15的奇数):");
scanf("%d", &n);
if (n > 0 && n <= 15 && n % 2 != 0) //如果是1—15的奇数,跳出while循环
break;
else
printf("输入错误,请输入奇数\n");
}
// 将数字1放在第一行中间位置
a[0][n / 2] = 1;
i = 0;
j = n / 2;
// 从2开始填充魔方阵,直到n*n
for (k = 2; k <= n * n; k++)
{
//魔方阵规则:行减一、列加一
i = i - 1;
j = j + 1;
// 检查边界并调整位置
if (i < 0 && j > n - 1)
{
i = i + 2;
j = j - 1;
}
else
{
if (i < 0)
i = n - 1;
if (j > n - 1)
j = 0;
}
// 如果下一个位置已经被占用,则在当前行的下一列放置数字
if (a[i][j] != 0)
{
i = i + 2;
j = j - 1;
}
a[i][j] = k;
}
// 打印魔方阵
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
printf("%4d", a[i][j]);
printf("\n");
}
return 0;
}运行结果:

代码逻辑:
一.创建一个奇数阶矩阵
二.将第一个元素 1 填在第一行中间的位置
三.其它元素行逐减、列逐加,依次排列在矩阵中
四.如果下一个位置已经被占用,那么直接放置在上一个元素的正下方
具体情况:
虽然条件很清晰,但在排列时受矩阵的计算规则限制,需要用多个条件来满足不同位置上的排列
1.1→2 2. 2→ 3 3.3 → 4 4.6 →7
i 0 → -1 2 → 1 1 → 0 0 → -1
j 1 → 2 2 → 3 0 → 1 2 → 3
else if (j > n - 1) if (a[i][j] != 0) if (i < 0 && j > n - 1)
{ j = 0; i = i + 2; i = i + 2;
if (i < 0) j = j - 1; j = j - 1;
i = n - 1;
i = -1 < 0 j = 3 > 2 i = -1 < 0,j = 3 > 2
a[2][2] = 2 a[1][0] = 3 a[2][0] = 4 a[2][1] = 7
8. 找出一个二维数组中的鞍点,即该位置上的元素在该行上最大,在该列上最小,也可能没有鞍点。
#include <stdio.h>
#define M 4 // 列数
#define N 3 // 行数
int main()
{
int i, j, k, a[N][M], max, maxj, flag;
// 输入数组
printf("请输入%d行%d列的数组:\n", N, M);
for (i = 0; i < N; i++)
{
for (j = 0; j < M; j++)
{
scanf("%d", &a[i][j]);
}
}
//查找鞍点
for (i = 0; i < N; i++)
{
max = a[i][0]; //假设a[i][0]最大
maxj = 0; //max和maxj用于存储当前行的最大值及其列索引
for (j = 1; j < M; j++) // 从1开始迭代列,因为0已经比较过了
{
if (a[i][j] > max) //如果行中有元素大于max,那么替换max和列索引maxj
{
max = a[i][j];
maxj = j;
}
}
//假设找到了鞍点
flag = 1;
for (k = 0; k < N; k++)
{
if (k != i && a[k][maxj] <= max) // 如果其他行的元素在当前列中大于max,则不是鞍点
{
flag = 0;
break;
}
}
if (flag)
{
printf("鞍点为a[%d][%d]=%d\n", i, maxj, max);
break; // 找到鞍点后退出循环
}
}
//如果没有找到鞍点,flag = 0
if (!flag)
{
printf("该矩阵不存在鞍点!\n");
}
return 0;
}运行结果:


代码逻辑:
一.先把第0行第0列的第一个元素设置成最大值max,并标记它的列maxj
二.比较行中所有的元素,并迭代最大值max和它的列maxj
三.假设第0行的最大值max就是鞍点,用它和同列的元素进行比较,如果其他行的元素在当前列中大于max,则不是鞍点
1.标记第一行的最大值并记录它的列
//查找鞍点
for (i = 0; i < N; i++)
{
max = a[i][0]; //假设a[i][0]最大
maxj = 0; //max和maxj用于存储当前行的最大值及其列索引
2.遍历第一行,迭代最大值和列
for (j = 1; j < M; j++) // 从1开始迭代列,因为0已经比较过了
{
if (a[i][j] > max) //如果行中有元素大于max,那么替换max和列索引maxj
{
max = a[i][j];
maxj = j;
}
}
3.假设第一行的迭代的最大值为鞍点,与其他行同一列的元素进行比较
//假设找到了鞍点
flag = 1;
for (k = 0; k < N; k++)
{
if (k != i && a[k][maxj] <= max) //如果其他行的元素在当前列中大于max,则不是鞍点
{
flag = 0;
break;
}
}
4.如果flag = 1,打印鞍点。如果flag = 0,打印该矩阵不存在鞍点
if (flag)
{
printf("鞍点为a[%d][%d]=%d\n", i, maxj, max);
break; // 找到鞍点后退出循环
}
}
//如果没有找到鞍点,flag = 0
if (!flag)
{
printf("该矩阵不存在鞍点!\n");
}
9. 有15个数按由大到小顺序存放在一个数组中,输入一个数,要求用折半查找法找出该数是数组中第几个元素的值。如果该数不在数组中,则输出"无此数"。
9.1初始化一个数组(递减)并打印
int main()
{
int a[15] = { 0 };
int i, j;
//初始化数组
for (i = 0; i < 15; i++)
{
a[i] = 15 - i;
}
for (j = 0; j < 15; j++)
{
printf("%d ", a[j]);
}
return 0;
}运行结果:

9.1标准代码
int main()
{
int a[15] = { 0 };
int i, j, num, mid, left, right, index = -1;
//1.初始化数组
for (i = 0; i < 15; i++)
{
a[i] = 15 - i;
}
//2.存储一个数
printf("请输入你要查找的数:");
scanf("%d", &num);
//3.遍历循环,重新设置左右边界查找数
left = 0;
right = 14;
while(left <= right)
{
mid = left + (right - left) / 2;
//3.1如果要查找的数恰好等于中间值,令num的索引等于中间值
//if (num == a[mid])
//index = mid;
if (num == a[mid])
{
index = mid;
printf("要查找的数num的索引是:%d", index);
return 0; //退出程序
}
//3.2如果num小于中间值
else if (num < a[mid])
left = mid + 1; //重新定义左边界
//3.2如果num大于中间值
else
right = mid - 1; //重新定义右边界
}
//如果循环结束还没有找到元素,则输出未找到的消息
if (index == -1)
printf("要查找的数num=%d不在该数组里\n", num);
return 0;
}运行结果:


代码逻辑:
一.初始化一个递减的一维数组
二.存储要查找的数
三.通过条件判断语句,迭代左右边界查找num
1.设定while循环的条件
left = 0;
right = 14;
while(left <= right)
{
mid = left + (right - left) / 2;
2.如果要查找的数恰好等于中间值,令num的索引等于中间值
//if (num == mid)
//index = mid;
if (num == a[mid])
{
index = mid;
printf("要查找的数num的索引是:%d", index);
return 0; //退出程序
}
3.由于每次都会比较index == a[mid],所以重新定义边界的时候可以忽略mid所在的索引
//3.2如果num小于中间值
else if (num < a[mid])
left = mid + 1; //重新定义左边界
//3.2如果num大于中间值
else
right = mid - 1; //重新定义右边界
}
注:
1.折半查找法
折半查找法的工作原理基于对有序数组的划分。它将查找范围逐步缩小为两半,通过比较目标元素与中间位置元素的大小来确定目标元素可能存在的区域,然后在该区域继续进行查找。每次迭代都将查找范围缩小一半,直到找到目标元素或确定目标元素不在数组中。
2.mid中间值公式问题
mid = left + (right - left) / 2; //mid = (left + right) / 2 + 1;
在二分查找算法中,将 mid 设置为 mid = (left + right) / 2 + 1; 是不合适的,原因如下:
-
偏移中点:标准的二分查找算法通过计算中点
mid来将搜索区间分为两部分。当使用mid = (left + right) / 2(在整数除法中,这通常会得到区间内的下标)时,中点被精确地定位在left和right之间。但是,通过加1(即+ 1),您实际上将mid的位置向右移动了一个元素,这可能导致跳过正确的中点,并可能使算法无法正确找到目标元素。 -
潜在的数组越界:
mid = (left + right) / 2 + 1在left和right相邻(即right = left + 1)时可能会导致mid等于right + 1,这是一个越界索引,因为它超出了数组的最后一个元素。 -
逻辑错误:二分查找的关键在于每次迭代都将搜索区间减半,直到找到目标元素或搜索区间为空。通过偏移中点,您可能会破坏这种逻辑,导致算法无法正确地缩小搜索范围,或者在某些情况下,甚至可能无限循环(尽管这种情况在标准的二分查找中不太可能发生,因为每次迭代都会更新
left或right)。
因此,为了保持二分查找算法的正确性和效率,应该使用标准的 mid = (left + right) / 2(在C/C++等语言中,为了避免整数溢出,更安全的写法是 mid = left + (right - left) / 2)来计算中点,并根据比较结果正确地更新 left 和 right。
为什么 mid = left + (right - left) / 2; 可以避免溢出?
-
先计算差值:
right - left首先计算left和right之间的差值。这个差值一定小于或等于right,因此它不太可能接近int类型的最大值。 -
然后除以 2:将差值除以 2 得到的是
left和right之间中间位置相对于left的偏移量。由于这个偏移量是基于差值的,它不会很大,因此不会导致溢出。 -
最后加上
left:将上一步得到的偏移量加回到left上,得到的就是中间索引mid。由于left和偏移量都不会很大(至少不会大到足以导致溢出),因此这一步也是安全的。
3.index值的设置问题
int index = -1;
while(left <= right)
{
mid = left + (right - left) / 2; //mid = (left + right) / 2 + 1;
//3.1如果要查找的数恰好等于中间值,令num的索引等于中间值
//if (num == mid)
//index = mid;
if (num == a[mid])
{
index = mid;
printf("要查找的数num的索引是:%d", index);
return 0; //退出程序
}
//如果循环结束还没有找到元素,则输出未找到的消息
if (index == -1)
printf("要查找的数num=%d不在该数组里\n", num);
return 0;
}
10.有一篇文章,共有3行文字,每行有80个字符。要求分别统计出其中英文大写字母、小写字母、数字、空格以及其他字符的个数。
10.1输人一行字符,分别统计出其中英文字母、空格、数字和其它字符的个数。(第五章第4题)
#include <stdio.h>
int main()
{
char c;
int eng_char = 0, space_char = 0, digit_char = 0, other_char = 0; //分类定义
printf("请输入一行字符:");
while ((c = getchar()) != '\n') // 读取输入直到遇到换行符
{
if (c >= 'a' && c <= 'z' || c >= 'A' && c <= 'Z')
{
eng_char++;
}
else if (c == ' ')
{
space_char++;
}
else if (c >= '0' && c <= '9')
{
digit_char++;
}
else
{
other_char++;
}
}
printf("英文字母数量: %d\n", eng_char);
printf("空格数量: %d\n", space_char);
printf("数字数量: %d\n", digit_char);
printf("其他字符数量: %d\n", other_char);
return 0;
}10.2标准代码:
#include<stdio.h>
int main()
{
char text[3][80] = { 0 };
//分类定义
int Eng_char = 0, eng_char = 0, digit_char = 0, space_char = 0, other_char = 0;
int i = 0, j = 0;
// 获取一行文本
for (int i = 0; i < 3; i++)
{
printf("请输入一行文本 %d:\n", i + 1);
gets(text[i]);
for (j = 0; j < 80 && text[i][j] != '\n'; j++)
{
if (text[i][j] >= 'A' && text[i][j] <= 'Z')
Eng_char++;
else if (text[i][j] >= 'a' && text[i][j] <= 'z')
eng_char++;
else if (text[i][j] >= '0' && text[i][j] <= '9')
digit_char++;
else if (text[i][j] = ' ')
space_char++;
else
other_char++;
}
}
printf("大写英文字母数量: %d\n", Eng_char);
printf("小写英文字母数量: %d\n", eng_char);
printf("数字数量: %d\n", digit_char);
printf("空格数量: %d\n", space_char);
printf("其他字符数量: %d\n", other_char);
return 0;
}运行结果:

代码逻辑:
//分行输出文本
for (int i = 0; i < 3; i++)
{
printf("请输入一行文本 %d:\n", i + 1);
gets(text[i]);
//判断条件:j < 80 && text[i][j] != '\n';
for (j = 0; j < 80 && text[i][j] != '\n'; j++)
{
......
}
}
11.输出以下图案
11.1输出以下图案

#include <stdio.h>
int main()
{
int i = 0;
int j = 0;
char ch = '*';
char space = ' ';
// 上半部分(前4行)
for (i = 0; i < 4; i++)
{
for (int j = 0; j < 3 - i; j++) // 打印前导空格
{
printf("%c", space);
}
for (int j = 0; j < 2 * i + 1; j++) // 打印星号
{
printf("%c", ch);
}
printf("\n");
}
// 下半部分(后3行),与上半部分逻辑不完全相同
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < i + 1; j++)
{
printf("%c", space);
}
for (int j = 0; j < k < 5 - (i*2); j++)
{
printf("%c", ch);
}
printf("\n");
}
return 0;
}11.2

#include<stdio.h>
int main()
{
char a[] = { "* * * *" };
int i, j, k;
for (i = 0; i < 5; i++)
{
for (j = 0; j < i; j++)
{
printf(" ");
}
for (k = 0; k < 7; k++)
{
printf("%c", a[k]);
}
printf("\n");
}
return 0;
}代码逻辑:
1.打印五行
for (i = 0; i < 5; i++)
{
2.打印空格
具体情况:
i = 0, j = 0不满足第一个子循环条件 j < i,直接进入第二个子循环打印****
i = 1, j = 0,进入第一个子循环,打印一个空格后j++ = 1(不满足条件)进入第二个子循环
......
每回循环结束时都打印一个换行符
for (j = 0; j < i; j++) //打印空格
{
printf(" ");
}
for (k = 0; k < 7; k++) //打印星号
{
printf("%c", a[k]);
}
printf("\n"); //打印换行符
}
运行结果:

12.有一行电文,以按下面规律译成密码:即第1个字母编程第26个字母,第i个字母编程第(26-i+1)个字母,非字母字符不变,要求编程序将密码 译回原文,并输出密码和原文。

#include<stdio.h>
int main()
{
char s[20] = { 0 };
int i = 0;
gets(s);
int len = strlen(s);
// 转换
for (int i = 0; i < len; i++)
{
// 1. 先用s[i] - 'a'计算出s[i]是26个字母中从前往后数的第几个
// 2. 再用26 - (s[i]- 'a') - 1 转换为26个字母中从后往前数的第几个
// 3. 在2的结果上加上'a',即转换为对应从后往前的第几个字母
if (s[i] >= 'a' && s[i] <= 'z')
s[i] = 'a' + 26 - (s[i] - 'a') - 1;
else if (s[i] >= 'A' && s[i] <= 'Z')
s[i] = 'A' + 26 - (s[i] - 'A') - 1;
}
printf("%s", s);
return 0;
}运行结果:

代码逻辑:
s[i] = 'a' + 26 - (s[i] - 'a') - 1;
1. 先用s[i] - 'a'计算出s[i]是26个字母中从前往后数的第几个
2. 再用26 - (s[i]- 'a') - 1 转换为26个字母中从后往前数的第几个
3. 在2的结果上加上'a',即转换为对应从后往前的第几个字母
for (int i = 0; i < len; i++)
{
if (s[i] >= 'a' && s[i] <= 'z')
s[i] = 'a' + 26 - (s[i] - 'a') - 1;
else if (s[i] >= 'A' && s[i] <= 'Z')
s[i] = 'A' + 26 - (s[i] - 'A') - 1;
}
13. 编一程序,将两个字符串连接起来,不要用strcat函数
#include<stdio.h>
int main()
{
char s1[10] = { 0 }; //保证被连接的数组s1空间足够大
char s2[5] = { 0 };
int index1 = 0;
int index2 = 0;
printf("请输入字符串s1:");
gets(s1); //排除了scanf识别不了空格的情况
printf("请输入字符串s2:");
gets(s2);
// 1.//循环遍历s1,直到找到结束符\0,此时index1 = 3
while ('\0' != s1[index1])
{
index1++;
}
// 2. 将s2中的字符逐个往s1之后拼接,直到遇到s2中的\0结束
while (s1[index1++] = s2[index2++]);
printf("将s2拼接在s1之后: ");
printf("%s\n", s1);
return 0;
}运行结果:

代码逻辑:
1.找到s1的末尾,并用index标记
while ('\0' != s1[index1])
{
index1++;
}
- 初始时,index1 = 0。
- 第一次循环迭代:检查s1[0],它是'a',不等于\0,所以循环继续,index1自增1,变为1。
- 第二次循环迭代:检查s1[1],它是'b',不等于\0,所以循环继续,index1自增1,变为2。
- 第三次循环迭代:检查s1[2],它是'c',不等于\0,所以循环继续,index1自增1,变为3。
- 第四次循环迭代:检查s1[3],它是\0,等于\0,所以循环结束
2.将s2开头标记为Index2并赋值给index1,达到连接的目的。当index2检索到s2的\0处结束循环
while (s1[index1++] = s2[index2++]);
· 第一次迭代:
- s1[index1] = s2[index2],即s1[3] = s2[0],所以s1[3]变为'e'。
- 然后,index1和index2都自增1。现在,index1 = 4,index2 = 1。
· 第二次迭代:
- s1[index1] = s2[index2],即s1[4] = s2[1],所以s1[4]变为'f'。
- 然后,index1和index2都再次自增1。现在,index1 = 5,index2 = 2
注:
1.关于while循环表达式的条件问题
直到s2[index2]是字符串结束符\0(此时赋值表达式的结果为0,即假,循环结束)
14. 编写一个程序,将连个字符串s1和s2比较,如果s1 > s2,输出一个整数;若s1 = s2,输出0;若s1 < s2,输出一个负数。不要用strcpy函数。两个字符串用gets函数读入。输出的正数或负数的绝对值应是相比较的两个字符串相对应字符的ASCII码的差值。例如,"A"和“C”相比,由于"A" < "C",应输出负数,同时由于‘A’与‘C’的ASCII码差值为2,因此应输出"-2"。同理:“And” 和"Aid"相比较,根据第2个字符比较结果,"n"比"i"大5,因此应输出"5"。
14.1 取反运算符
#include <stdio.h>
int main()
{
int i = 0, j = 0;
i = (!(j = 0)); //j = 0,取反后i = 1
printf("%d", i);
return 0;
}
运行结果:

标准代码:
#include <stdio.h>
int main()
{
int ret = 0;
int index = 0;
char s1[100] = { 0 };
char s2[100] = { 0 };
printf("请输入s1:\n");
gets(s1);
printf("请输入s2:\n");
gets(s2);
//while的条件为1才会进入循环体
while (!(ret = s1[index] - s2[index]) && s1[index] != '\0' && s2[index] != '\0')
{
index++; //继续比较下一个元素
}
printf("%d\n", ret);
return 0;
}
运行结果:


代码逻辑:
一.当while循环中的判断条件结果为1时,才进入循环
二.比较字符串是否相等、如果到达结尾立刻退出循环
1.取反运算符
!(ret = s1[index] - s2[index]) //当两个元素相等时ret = 0,!ret = 1。继续循环
2.只要碰到结尾\0立刻退出循环
s1[index] != '\0' && s2[index] != '\0'
3.同时满足这两个条件(3个)while循环里的值才为1
while (!(ret = s1[index] - s2[index]) && s1[index] != '\0' && s2[index] != '\0')
{
index++; //继续比较下一个元素
}
15.编写一个程序,将字符数组s2中的全部字符复制到字符数组s1中,不用strcpy函数。复制时,‘\0’也要赋值过去。'\0'之后的字符不复制。
#include<stdio.h>
int main()
{
char s1[100] = { 'a', 'b', 'c' };
char s2[50] = { 0 };
int index1 = 0;
int index2 = 0;
printf("请输入字符串s2:");
gets(s2);
// 将s2[index2]位置字符拷贝到s1[index]位置,
// 然后以s1[index1]的值作为循环条件判断
// 是否拷贝到s2的末尾
while (s1[index1++] = s2[index2++]);
printf("将s2拷贝到s1中,s1现在为:%s\n", s1);
return 0;
}运行结果:

代码逻辑:
使用while循环进行字符串复制。循环的条件是s1[index1++] = s2[index2++];,这是一个赋值表达式,它将s2[index2]的值赋给s1[index1],然后同时自增index1和index2。循环会一直执行,直到s2[index2]是字符串结束符\0(此时赋值表达式的结果为0,即假,循环结束)
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








