整数分块

一般在算法中遇到时间复杂度为
1e9的, 那么一次 O ( n ) O(n) O(n)的遍历无法解决问题
求== ∑ i = 1 n [ n i ] \sum_{i=1}^n{[\frac{n}{i}]} ∑i=1n[in]==





例题1:因数平方和

分析:
要求 n n n的约数,时间复杂度肯定不够, 所以想到反着求
a是b的约数 <==> b是a的倍数,所以我们只需要求哪些数包含约数a相加
每一个约数a 对答案的贡献度为
a
2
a^2
a2, 每个数a是
n
a
\frac{n}{a}
an个数的约数
故a这个数对答案的总贡献为
a
2
∗
[
n
a
]
a^2\ *\ [\frac{n}{a}]
a2 ∗ [an],故答案为:
∑
i
=
1
n
[
n
i
]
∗
i
2
\sum_{i=1}^n\ [\frac{n}{i}]*i^2
i=1∑n [in]∗i2

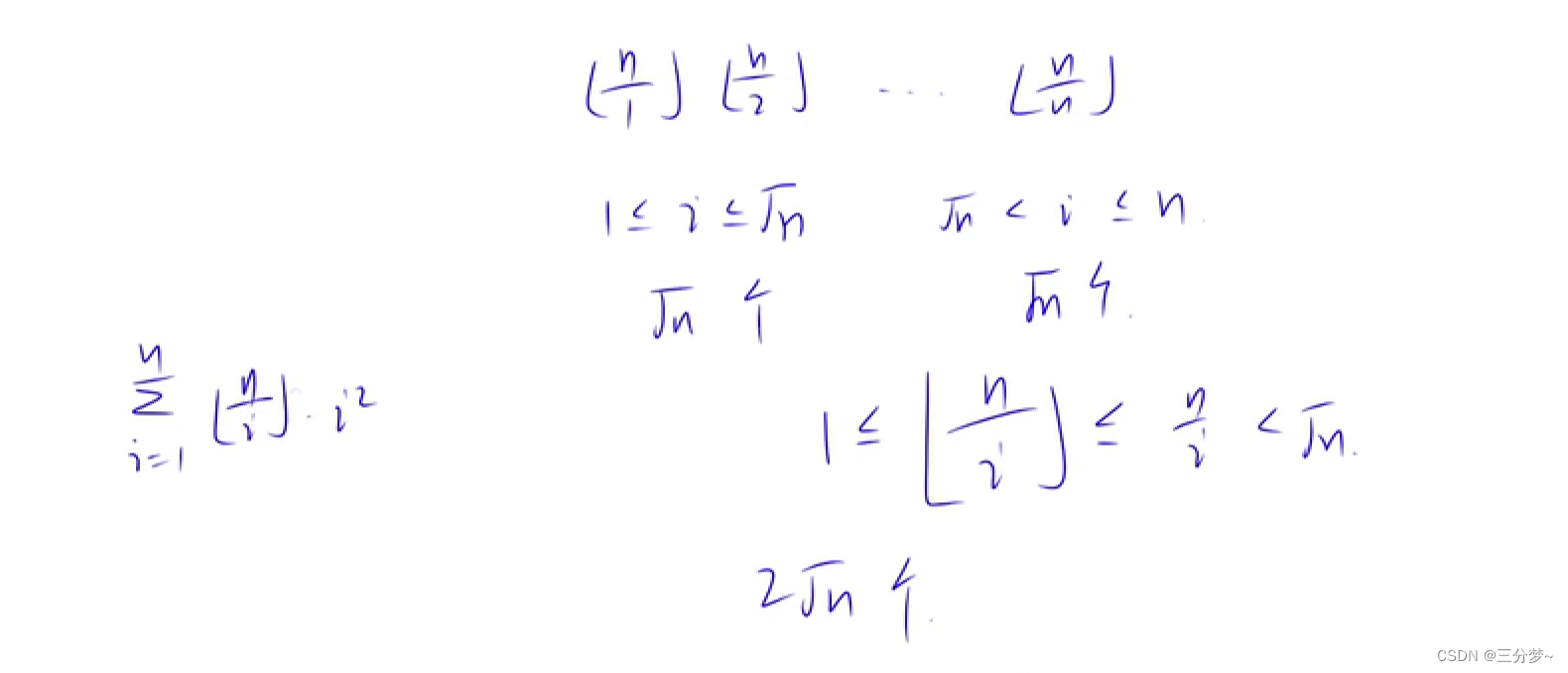
由上可知, 可以将n划分为前半段和后半段的话, 可计算出只需操作
2
n
2\sqrt{n}
2n个数即可
如此, 可以将 n n n优化为 2 n 2\sqrt{n} 2n个数进行计算
进行分块治理,如下

将区间长度为 n n n划分为 2 n 2\sqrt{n} 2n个区间, 对每个区间进行求值,每个区间值相同, 只需算连续平方和,可以直接用公式求平方和值, 故每个区间只需要算一次即可
结果: O ( N ) − − > O ( N 2 ) O(N) - - > O(N^2) O(N)−−>O(N2)

推导出:每个区间最大的位置: y = n / x y = n / x y=n/x , 对于各个区间值为== x = n / i x = n / i x=n/i==
即计算区间和每个== [ i , y ] [i, y] [i,y]区间即可, 然后算完一个区间直接 i = y + 1 i = y + 1 i=y+1,来跳跃到下一个区间进行计算, 总共只需要算 2 n 2\sqrt{n} 2n==次
具体代码:
此题在计算平方和时可能数据量会超大(超LL)
__int128写法
#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
//__int128 : 2^127 - 1
LL calc(int n) { //计算平方和
//这里可能特别大超过2^64(LL),故用__int128临时存储数值
return n * (__int128)(n + 1) * (2*n + 1) / 6 % MOD;
}
int main() {
int n;
cin >> n;
LL res = 0;
for(int i = 1; i <= n; ) {
//划分为2sqrt(n)个区间,每个区间的所有数相等,第i个区间值为n/i
int x = n / i, y = n / x;
//求区间[i, y]的平方和,再乘上x值
res = res + x * (calc(y) - calc(i - 1)) % MOD;
i = y + 1;
}
//这块可能取模相减为负值,故
cout << (res + MOD) % MOD << endl;
return 0;
}
逆元写法
LL calc(int n) { //计算平方和
//这里可能特别大超过2^64(LL),故用__int128临时存储数值
// return n * (LL)(n + 1) * (2*n + 1) / 6 % MOD;
//逆元写法
return n * (LL)(n + 1) % MOD * (2*n + 1) % MOD * 166666668 % MOD;
}
//计算 /6 的逆元
/for(int i = 1; ;i++) { //算出逆元答案为166666668, 带入上式替换掉 '/6'
if(i * 6 % MOD == 1) {
cout << i << endl;
return 0;
}
}
例题2:余数之和

思想:
首先看到数据范围为1e9级别,故可以想到用分块思想,优化到 O ( 2 n ) O(2\sqrt{n}) O(2n)
k % i k \% i k%i <==> k − [ k i ] ∗ i k - [\frac{k}{i}]*i k−[ik]∗i
则 k % ∑ 1 n k \% \sum_1^n k%∑1n < = = > <==> <==> n ∗ k − ∑ i = 1 n [ k i ] ∗ i n*k\ -\ \sum_{i=1}^n[\frac{k}{i}]*i n∗k − ∑i=1n[ik]∗i
代码
#include <iostream>
using namespace std;
typedef long long LL;
LL sum_primes(int n, int k) {
//k % i = k - [k / i] * i ---> k % [1, n] = n*k - k / [1,n]*i
LL res = (LL)n * k;
for(int i = 1; i <= n; ) {
if(k < i) break; //此时往后全为0,不用操作了
int x = k / i, y = min(k / x, n); //区间有极限值为n,防止越界
//求区间总值 * x --- > 等差数列求和:n * (a1 + an) / 2
res -= x * (LL)(y - i + 1) * (i + y) / 2;
i = y + 1; //操作下一个区间
}
return res;
}
int main() {
int n, k;
cin >> n >> k;
cout << sum_primes(n, k) << endl;
return 0;
}





















 1316
1316











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








