数据结构与算法（基础版）
视频地址：https://www.bilibili.com/video/BV13g41157hK?t=2.3&p=3
一.时间复杂度及排序算法
1.master公式(算递归时间复杂度)：
T(N) = a*T(N/b) + O(N^d)
1) log(b,a) > d -> 复杂度为O(N^log(b,a) )
2) log(b,a) = d -> 复杂度为O(N^d *logN)
3) log(b,a) < d -> 复杂度为O(N^d)
补充阅读：www.gocalf.com/blog/algorithm-complexity-and-master-theorem.html
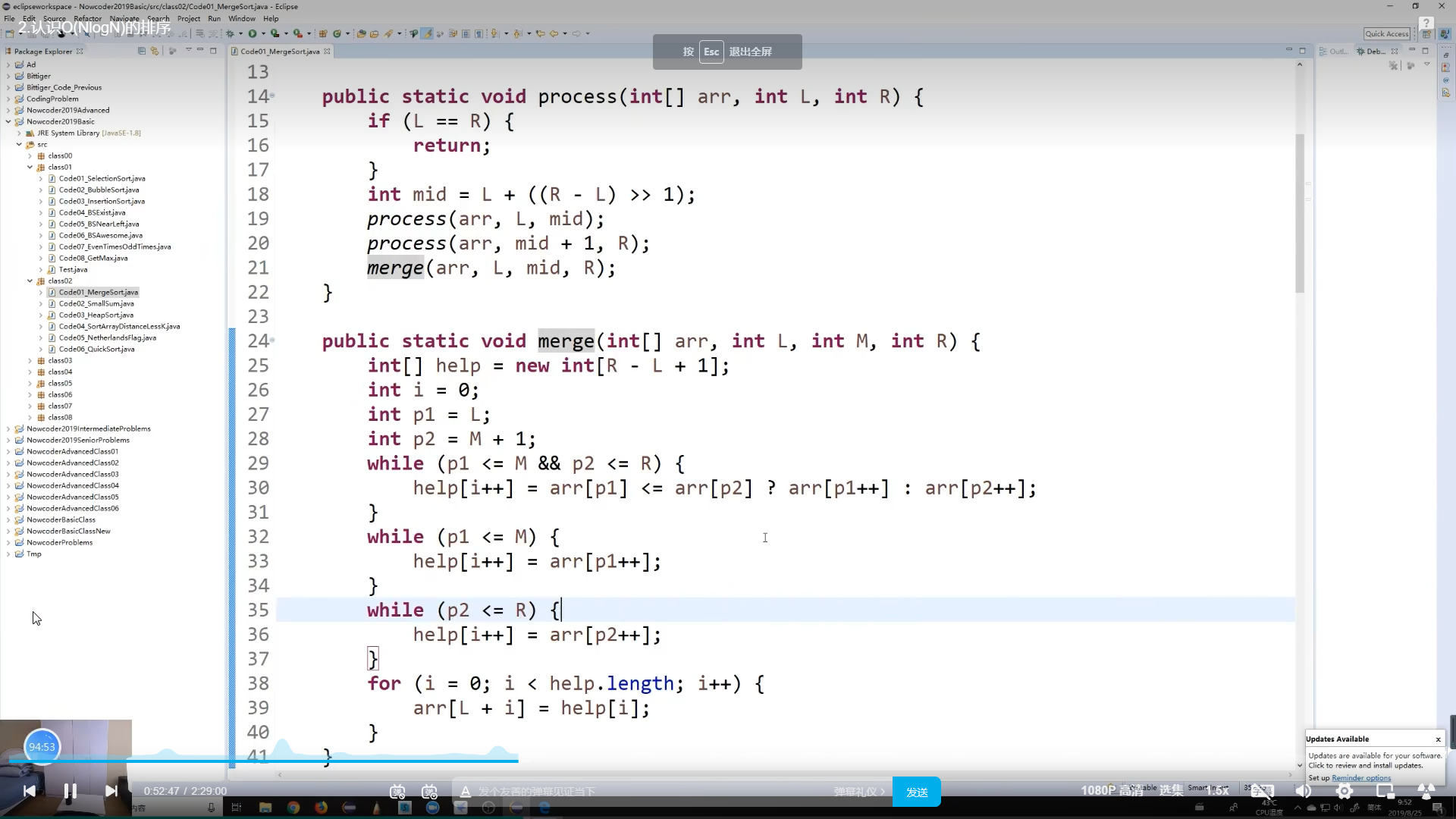
2.归并排序（时间复杂度为O(N*logN)）
（找小和问题）：分成左右两边，递归成两边分别有序，双指针从左往右，从小到大复制到help数组
3.快速排序（可优化至O(N*logN)）
（荷兰国旗问题）：分批次递归，把目标值按在中间
① 快排 1.0 和 2.0 时间复杂度均为O(N^2)，这里不赘述
② 快排3.0时间复杂度数学期望为O(N*logN)
package chapter.class01;
import java.util.Arrays;
public class main {
public static void main(String[] args) {
int[] arr={1,6,7,8,3,5,6,7,3};
quickSort(arr);
for(int i=0;i<arr.length;i++) {
System.out.println(arr[i]);
}
}
public static void quickSort(int[] arr){
if(arr == null || arr.length<2){
return;
}
quickSort(arr , 0 , arr.length-1);
}
public static void quickSort(int[] arr,int L,int R){
if(L<R){
swap(arr,L + (int)(Math.random() * (R-L+1)), R);
int[] p = partition(arr,L,R);
quickSort(arr,L,p[0]-1);// <区
quickSort(arr,p[1]+1,R);// >区
}
}
//此函数返回一个长度为二的数组res，res[0]为左边界，res[1]为右边界
public static int[] partition(int[] arr,int L,int R){
int less = L-1;// <区右边界
int more = R;// >区左边界
while(L<more){// L表示当前数的位置 ，arr[R] --》划分值
if(arr[L]<arr[R]){// 当前数 < 划分值
swap(arr,++less,L++);
}else if(arr[L]>arr[R]){// 当前数 > 划分值
swap(arr,--more,L);
}else{
L++;
}
}
swap(arr,more,R);
return new int[] {less+1,more};
}
public static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
4.堆排序
①通过heapinsert和heapify 来进行反复找最大值放在堆尾
package chapter.class01;
public class class01_heapSort {
public static void main(String[] args) {
int[] arr={7,4,4,6,3,0,7,1,3,9};
heapSort(arr);
}
public static void heapSort(int[] arr){
if(arr == null|| arr.length < 2){
return;
}
for(int i=0;i<arr.length;i++){
heapInsert(arr,i);
}
int heapSize = arr.length;
swap(arr,0,--heapSize);
while(heapSize > 0){
heapify(arr,0,heapSize);
swap(arr,0,--heapSize);
}
}
//某个数在index位置，往上继续移动
public static void heapInsert(int[] arr,int index){
while(arr[index] > arr[(index - 1) / 2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
//某个数在index位置，能否往下移动
public static void heapify(int[] arr,int index,int heapSize){
int left = index*2+1;//左孩子的下标
while(left < heapSize){//下方还有孩子的时候
//两个孩子中，谁的值大，把下标给largest
int largest = left+1<heapSize && arr[left+1] > arr[left] ? left +1 :left;
//父和较大的的孩子之间，谁的值大，把下表给largest
largest = arr[largest] > arr[index] ? largest : index;
if(largest == index){
break;
}
swap(arr,largest,index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}5.比较器（Java特有）
（没咋听懂，后面再看）
6.总结
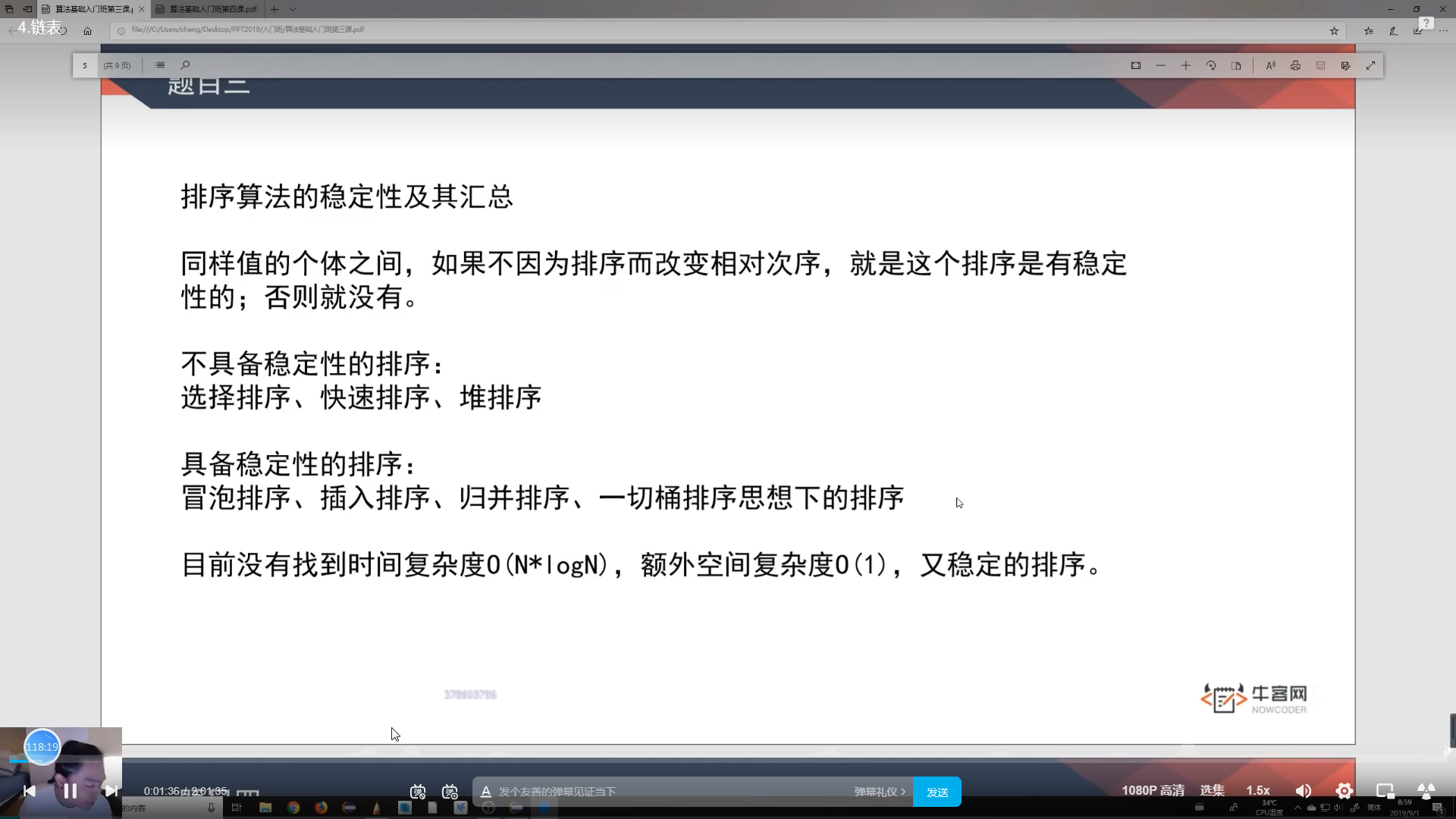
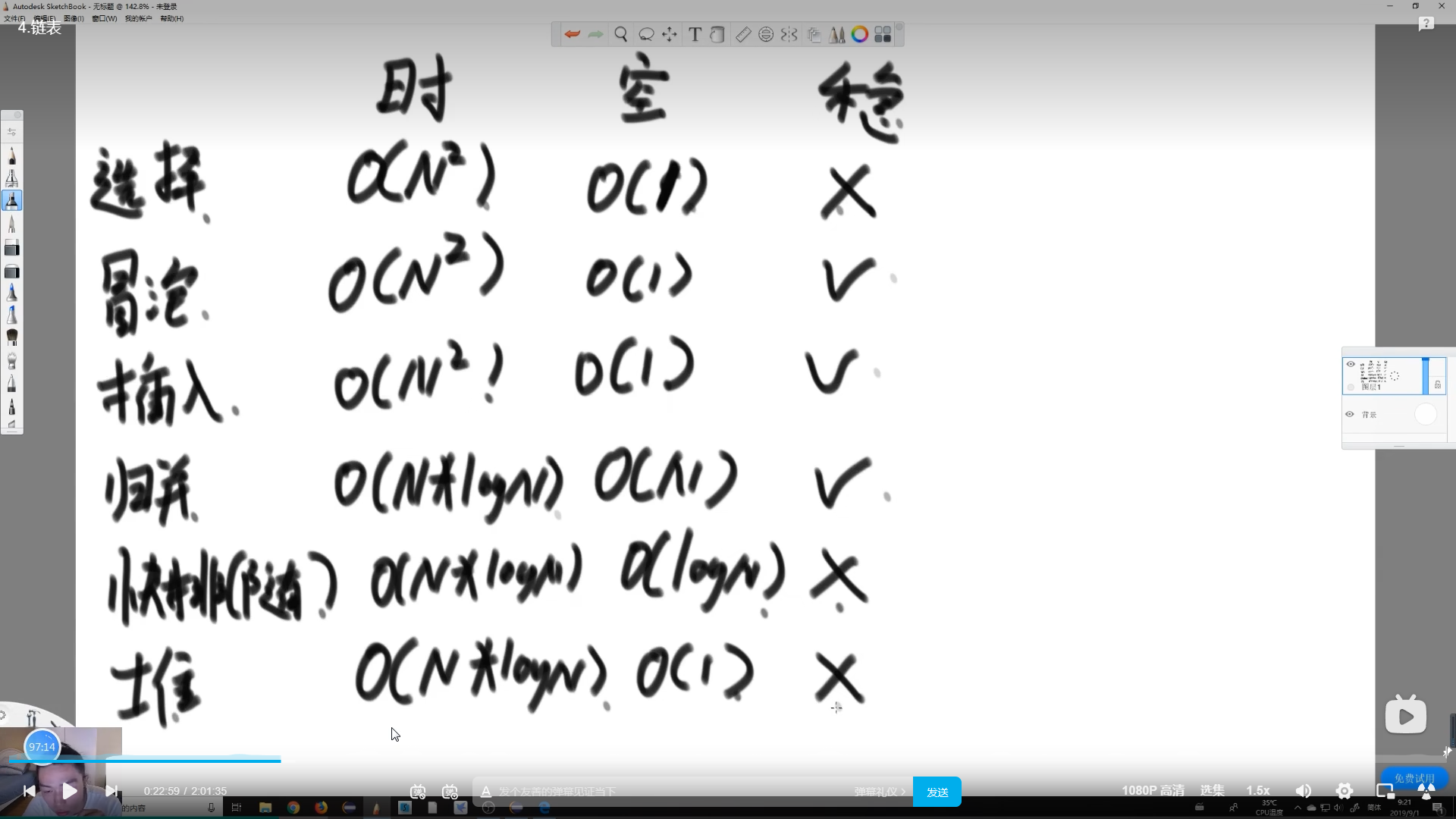
快排最快，堆排所需空间少，归并稳定
二.链表
1.哈希表
2.有序表
与哈希表区别：时间复杂度更高，元素有序（个人理解）
3.链表（此部分内容大部分为coding问题）
三.二叉树
1.用递归和非递归两种方式实现先序，中序，后序遍历
（1）递归：
递归序：每个节点会三次回到自己，在此基础上引申出了先序，中序，和后序遍历
①先序遍历（头左右）：在递归序的基础上，第一次出现时打印（或进行操作）
public static void preOrderRecur(Node head){
if(head == null){
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
②中序遍历（左头右）：在递归序的基础上，第二次出现时打印（或进行操作）
public static void inOrderRecur(Node head){
if(head == null){
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}③后序遍历（左右头）：在递归序的基础上，第三次出现时打印（或进行操作）
public static void posOrderRecur(Node head){
if(head == null){
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}（2）非递归：
①先序遍历（同上）：
第一步：从栈中弹出一个节点car；
第二步：打印（或处理）car；
第三步：先压右再压左（如果有的话），没有就不操作；
第四步：重复上述步骤；
public static void preOrderUnRecur(Node head){
if(head != null){
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while(!stack.isEmpty()){
head = stack.pop();
System.out.print(head.value + " ");
if(head.right != null){
stack.push(head.right);
}
if(head.left != null){
stack.push(head.left);
}
}
}
System.out.println();
}②中序遍历（同上）：
第一步：对于每一颗子树，左边界全部进栈（从父到子）；
第二步：依次弹出的过程中，打印；
第三步：弹出节点的右树重复上述步骤（如果有的话）；
public static void inOrderUnRecur(Node head){
if(head != null){
Stack<Node> stack = new Stack<Node>();
while(!stack.isEmpty() || head != null){
if(head != null){
stack.push(head);
head = head.left;
}else{
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}③后序遍历（同上）：（略有不同的地方是，用了两个栈）
此方法本质（个人理解）：利用栈的特点，从头右左的遍历顺序逆序出 栈，变成左右头。
第一步：从栈中弹出一个节点car；
第二步：car放入收集栈；
第三步：先压左再压右；
第四步：重复上述步骤；
public static void posOrderUnRecur(Node head){
if(head != null){
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while(!s1.isEmpty()){
head = s1.pop();
s2.push(head);
if(head.left != null){
s1.push(head.left);
}
if(head.right != null){
s1.push(head.right);
}
}
while(!s2.isEmpty()){
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}2.完成二叉树的宽度优先遍历（宽度遍历用队列）
二叉树的深度优先遍历即是先序遍历；
①从队列弹出一个节点；
②先放左，再放右；
public static void widthFirstOrder(Node head){
if(head == null){
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.value);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}3.二叉树的相关概念
①搜索二叉树（BST）：对于每一棵子树，它的左树都比它小，右树都比它大；
②如何判断搜索二叉树：中序遍历，如果某个位置存在降序，则不是搜索二叉树，即搜索二叉树中序遍历结果一定是升序；
第一种代码：
public static int preValue = Integer.MIN_VALUE;//设置一个全局变量用来比较是否为升序；此语句意为整数（Integer）的最小值
public static boolean checkBST(Node head){
if(head == null){
return true;//如果树为空，认为是搜索二叉树
}
boolean isLeftBST = checkBST(head.left);//判断左边是否为搜索二叉树，将结果返回给变量用于后续判断
if(!isLeftBST){
return false;//如果左边已经不为搜索二叉树，则直接返回false
}
if(head.value <= preValue){
return false;//如果左边树的最后一个节点比preValue小的话，则不为升序，直接返回false
}else{
preValue = head.value;//如果大于的话，那就赋值给preValue，相当于将其作为指针遍历下去（个人理解）
}
return checkBST(head.right);//右树结果直接返回
}第二种代码（运用递归思想）：
public static boolean isBST(Node head){
return process(head).isBST;
}
public static class ReturnData{
public boolean isBST;
public int min;
public int max;
public ReturnData(boolean is,int mi,int ma){
isBST = is;
min = mi;
max = ma;
}
}
public static ReturnData process(Node x){
if(x == null){
return null;
}
ReturnData leftData = process(x.left);
ReturnData rightData = process(x.right);
//找最值
int min = x.value;
int max = x.value;
if(leftData != null){
min = Math.min(min, leftData.min);
max = Math.max(max, leftData.max);
}
if(rightData != null){
min = Math.min(min, rightData.min);
max = Math.max(max, rightData.max);
}
//判断isBST
//第一种方法：
boolean isBST = true;
if(leftData!=null && (!leftData.isBST || leftData.max >= x.value)){
//如果左树有东西，且左树不为搜索二叉树，则直接false，或者如果左树有东西，且左树的最大值比根节点的值大，也直接 false
isBST = false;
}
if(rightData != null && (!rightData.isBST || x.value >= rightData.min)){
//同上面的思路，如果右树有东西，且右树不为搜索二叉树，则直接false，或者如果右树有东西，且右树的最小值比根节点的值 小，则直接false
isBST = false;
}
//第二种方法：
/*boolean isBST = false;
if(
(leftData!=null ? (leftData.isBST && leftData.max < x.value):true)
&&
(rightData != null ? (rightData.isBST && rightData.min > x.value) : true)
){
isBST = true;
}*/
return new ReturnData(isBST,min,max);//返回三个数据，是否为搜索二叉树，树的最小值与最大值
}①完全二叉树（CBT）：每一层都是满的或者最后一层不满但从左到右是满的（比较拗口，建议去百度一手）
②如何判断完全二叉树：宽度优先遍历，（1）对于任意节点，如果有右无左直接false；（2）在（1）条件满足的情况下，如果第一次遇到了一个节点左右子不全（其实就是只有左节点或者本身为叶节点），那么后续节点必须全为叶节点（无子节点），如果不满足，则不为完全二叉树
public static boolean isCBT(Node head){
if(head == null){
return true;
}
LinkedList<Node> queue = new LinkedList<>();
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while(!queue.isEmpty()){
head = queue.poll();
l = head.left;
r = head.right;
if((leaf && (l != null || r != null))||(l ==null && r != null)){
return false;
}
if(l != null){
queue.add(l);
}
if(r != null){
queue.add(r);
}
if(l == null || r == null){
leaf = true;
}
}
return true;
}3.①满二叉树：一棵高度为h，并且含有2^h - 1个结点的二叉树称为满二叉树，即树中的每一层都含有最多的结点。满二叉树的叶子节点都集中在二叉树的最下一层，并且除叶子结点之外的每个结点度数均为2.(二叉树结点的度即为结点的孩子个数);
②如何判断满二叉树：可以直接根据定义，先求树的最大深度h，再求节点个数s，需要满足s=2^h-1;
public static boolean isFBT(Node head){
if(head == null){
return true;
}
ReturnData data = process(head);
return data.nodes == (1<<data.height - 1);
}
public static class ReturnData{
public static int height;
public static int nodes;
public ReturnData(int h,int n){
height = h;
nodes = n;
}
}
public static ReturnData process(Node x){
if(x == null){
return new ReturnData(0,0);
}
ReturnData leftData = process(x.left);
ReturnData rightData = process(x.right);
int height = Math.max(leftData.height,rightData.height)+1;
int nodes = leftData.nodes+rightData.nodes+1;
return new ReturnData(height,nodes);
}4.①平衡二叉树（AVL）：对于任何一个子树，它的左树和右树高度差不超过1；
②如何判断平衡二叉树：首先需要满足根节点左树和右树都为平衡二叉树，再要满足左树的高度与右树的高度差不大于1；
public static boolean isBalanced(Node head){
return process(head).isBalanced;
}
public static class ReturnType{
public boolean isBalanced;
public int height;
public ReturnType(boolean isB,int hei){
isBalanced = isB;
height = hei;
}
}
public static ReturnType process(Node x){
if(x == null){
return new ReturnType(true,0);
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int height = Math.max(leftData.height, rightData.height) + 1;
boolean isBalanced = leftData.isBalanced && rightData.isBalanced && Math.abs(leftData.height - rightData.height)<2;
return new ReturnType(isBalanced,height);
}
7714
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
