m/2个人拉m盏灯后求灯的状态问题

在m个人拉m盏灯后求灯的状态问题-CSDN博客中介绍了m个人拉m盏灯的问题。下边介绍一下m/2个人拉m盏灯的问题。

题目：

有m盏灯，编号分别为1，2，3，...，m，每拉一次灯的开关，灯的亮灭状态就发生一次变化。这m盏灯初始状态都是亮着的，有m/2个人去拉灯，第1个人把所有的灯都拉一次，第2个人把编号是3的倍数的灯拉都拉一次，第3个人把编号是5的倍数的灯都拉一次，...，第m/2个人把编号是(m/2)*2+1的灯都拉一次。问：最终哪些编号的灯是灭的？

本题和上一解题目的区别是：上一节的题目是求灯编号i的所有因数为奇数的情况，这个题目是找灯编号i的奇因数为奇数的情况。

一、编程方法一

我们先用上一节的编程方法一的思路来进行求解一下。

第一步：声明一个整形变量m，由键盘输入m的具体值。

第二步：声明一个有m+1个元素的布尔型数组，其中脚标为1到m的元素用于存储m盏灯的亮灭状态，亮为1，灭为0。

第三步：用for循环求解当所有人都拉过一次灯后，灯的状态。这一步是关键，灯的序号用i表示，人的序号用j表示，从i=1开始到m结束，循环求解j=1开始到m结束，增加步伐为2时(因为拉的灯的编号都为奇数的倍数)，i是否是j的倍数，如果是则序号为i的灯状态翻转一次。

第四部：把状态为灭的灯的序号输出。

具体代码如下：

#include <iostream>
using namespace std;
 
int main()
{
    int m;    //声明m盏灯
    cin>>m;    //键盘输入m的具体数值    
    bool lamp_status[m+1];    //声明存储灯状态的布尔型变量数组，1为亮，0为灭
 
    for(int i=1;i<=m;i++)    //循环求解i盏灯的状态
        {
            lamp_status[i]=1;    //灯的初始状态为亮
            for(int j=1;j<=m;j+=2)    //循环求解第j个人拉灯之后，灯的状态变化，j只能为奇数，所以增加步伐为2
                {
                    if(i%j==0)        //如果i是j的倍数，则灯的状态进行翻转
                    lamp_status[i]=!lamp_status[i];
                }
                
            if(lamp_status[i]==0)     //如果灯的状态为灭则输出灯的序号
                {
                    cout<<i<<endl;
                }
        } 
    return 0;
}

当m=100时，运算结果为：

1
2
4
8
9
16
18
25
32
36
49
50
64
72
81
98
100

观察发现，灯灭的编号比上一节的数量要多，但编号中仍然包含了所有的100以内的完全平方数{1，4，9，16，25，36，49，64，81，100}和非完全平方数{2，8，18，32，50，72，98}。再仔细观察，发现了一个更有趣的现象，这些非完全平方数恰好是前7个完全平方数{1，4，9，16，25，36，49}的2倍。

为了寻找规律，把m值增大到100，看以下运行结果。

1
2
4
8
9
16
18
25
32
36
49
50
64
72
81
98
100
121
128
144
162
169
196
200
225
242
256
288
289
324
338
361
392
400
441
450
484
512
529
576
578
625
648
676
722
729
784
800
841
882
900
961
968

可以发现，结果仍然是有两部分组成，一部分是完全平方数{1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529,576,625,676,729,784,841,900,961}，另外一部分是非完全平方数的2倍{2,8,18,32,50,72,98,128,162,200,242,288,338,392,450,512,578,648,722,800,882,968}。

看来这也是一个必然的规律，那么我下边还是来分析一下。

二、理论分析

1、首先来分析，为什么完全平方数的奇因数为奇数个

（1）第一种情况，完全平方数为奇数。

奇数的所有因数都是奇数，上一届分析过了，完全平方数的因数个数为奇数，也就是完全平方数为奇数时，其奇因数的个数一定是奇数。所以得出：

规律1：当完全平方数为奇数时，这个完全平方数的奇因数的个数为奇数。

（2）第二种情况，完全平方数为偶数。

假设这个偶数为，它的平方根为，假设可以分解为s个奇质因数和t个偶质因数之积，即，令，，则。如果存在奇因数，那么这个奇因数一定是的因数，而是一个完全平方数，而且是奇数，所以根据规律1，的奇因数，也就是的奇因数的个数一定是奇数。

所以综合以上两种情况得出：

规律2：完全平方数的奇因数的个数为奇数。

2、再来分析，完全平方数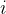的2倍的奇因数的个数

完全平方数的2倍=2*，2为偶数，且2中不包含奇因数，因此2*中奇因数只与有关，其奇因数的个数就是的奇因数的个数。根据规律2，得知完全平方数的2倍的奇因数个数也为奇数。

同理，可以推测，一个完全平方数乘以一个系数，如果这个的质因数中不包含奇数，那么的奇因数的个数也一定是奇数。而符合这个条件的只能是2的若干次幂，即(p为大于等于1的自然数)。如果为偶数，那么，仍然为一个平方数。如果为奇数，那么，其结果为一个完全平方数的2倍。

根据以上规律，可以得知，小于m的自然数中，其奇因数为奇数的情况只包括完全平方数和完全平方数的2倍这两种情况。这也与程序运算得出的结果相一致。

三、编程方法二

略

四、编程方法三

既然这样，那么我们就可以放心大胆地利用上一节的编程方法三来求解本节的问题了。

思路大致如下：

第一步，求出1到m内最大完全平方数对应的最大平方根。

第二步，求出1到m内的所有完全平方数。

第三步，求出1到m内的所有完全平方数的2倍。

第四步，输出所有符合要求的结果。

#include <iostream>
#include <math.h>
using namespace std;
 
int main()
{
    int m;    //声明m盏灯
    cin>>m;    //键盘输入m的具体数值
    int MaxsquarRoot=sqrt(m);       //求平方数为m的最大整数平方根，那么小于等于这个最大整数平方根的所有自然数的平方都是小于m的完全平方数。
    for(int i=1;i<=MaxsquarRoot;i++)    //循环求解i盏灯的状态
        {
            cout<<i*i<<endl;    //输出完全平方数
            if(i*i*2<=m)
            cout<<i*i*2<<endl;   //输出小于等于m的完全平方数的2倍
        } 
    return 0;
}

当m=100时，运行的结果如下：

1
2
4
8
9
18
16
32
25
50
36
72
49
98
64
81
100

运算结果与编程方法一一致，只是数字的排列顺序有些差异，有兴趣的C粉，可以把我的程序改进一下，能按由小到大的顺序输出。

（全文完）