牛郎织女式的爱情——双向搜索

一千个愿望,一千个计划,一千个决心,不如一个行动.

序言：双向搜索是DFS和BFS的一种进阶应用，其基本思想是从两个点同时向中间搜索，这样可以有效降低搜索的时间复杂度。双向搜索包括两种典型的算法：双向同时搜索和“meet in the middle”。

🍈双向同时搜索🍈

原理🍎

这个算法需要知道起点和终点。
双向同时搜索是指从一个图的两个点同时开始进行dfs或bfs，如果两个进度在一个点相撞，那么认为是找到了一个可行解。
该算法常被用于寻找点到点的最短路。
我们这里用bfs为例说明过程，但dfs是一样的。

图示🍉

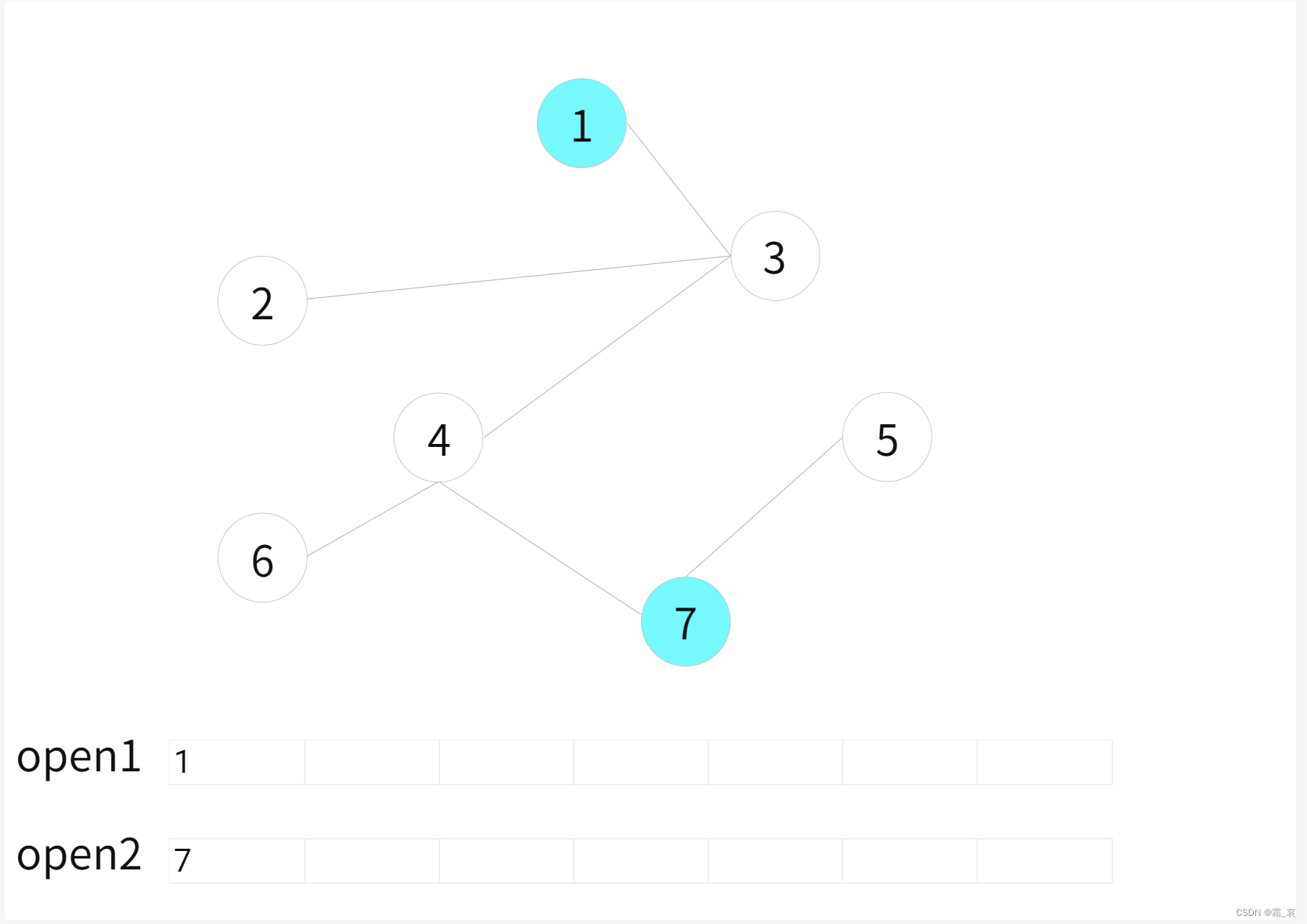
1. 原图，此刻要维护两个队列，命名为open1和open2，蓝色点是将要搜索的点
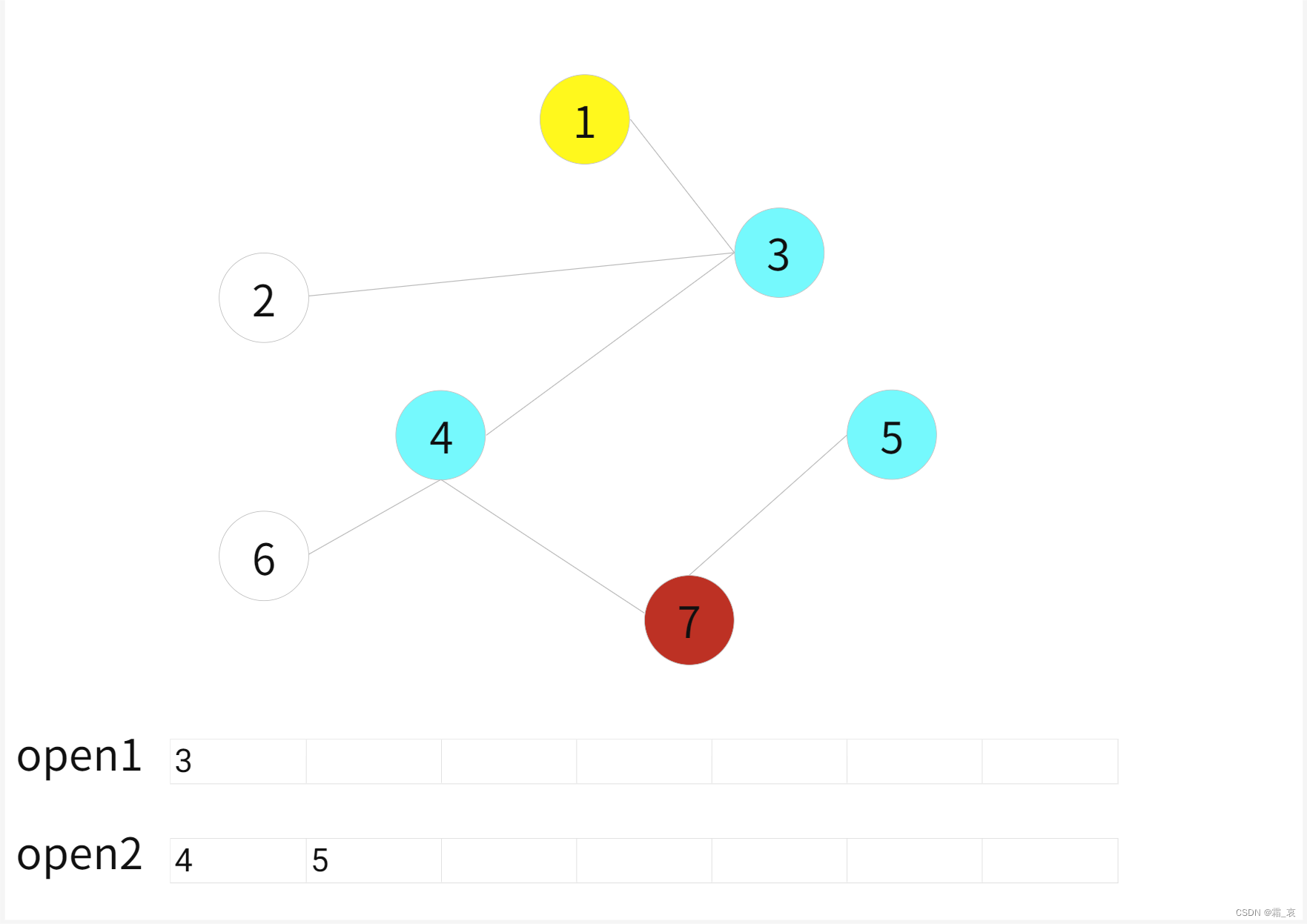
2. 两边都进行bfs，红色点是下面的bfs部分搜索过的点，黄色的是上面部分搜索过的。
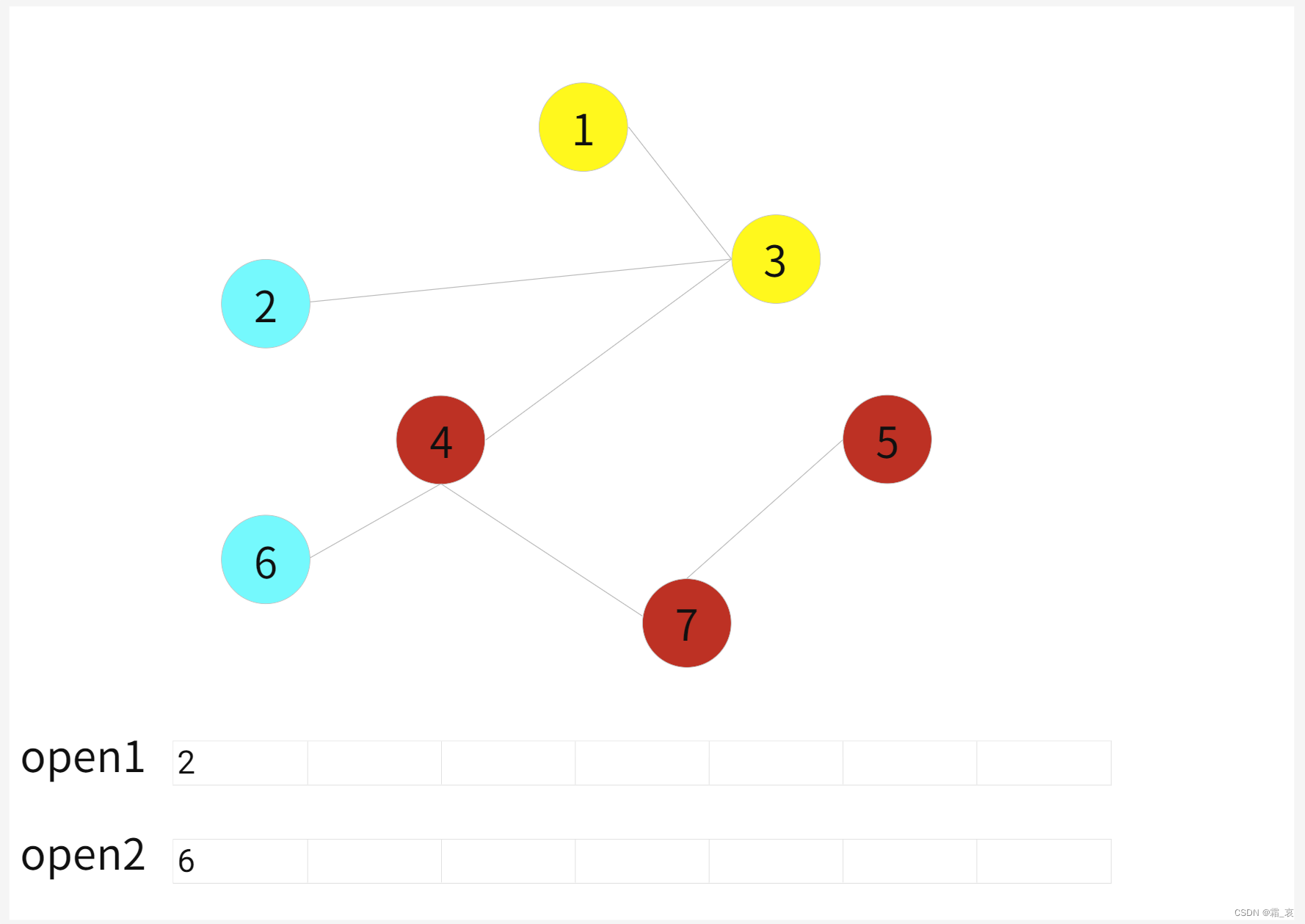
3. 4搜索完后寻找邻接点3，发现3已经被上面的bfs搜索过，于是判定两个bfs相撞，得到一个解。（注意，为了知道哪个结点是被哪个bfs搜索过的，需要多维护一个int数组，每个结点下标对应的值表示它被哪个bfs搜索过，未被搜索过则该值设为0）
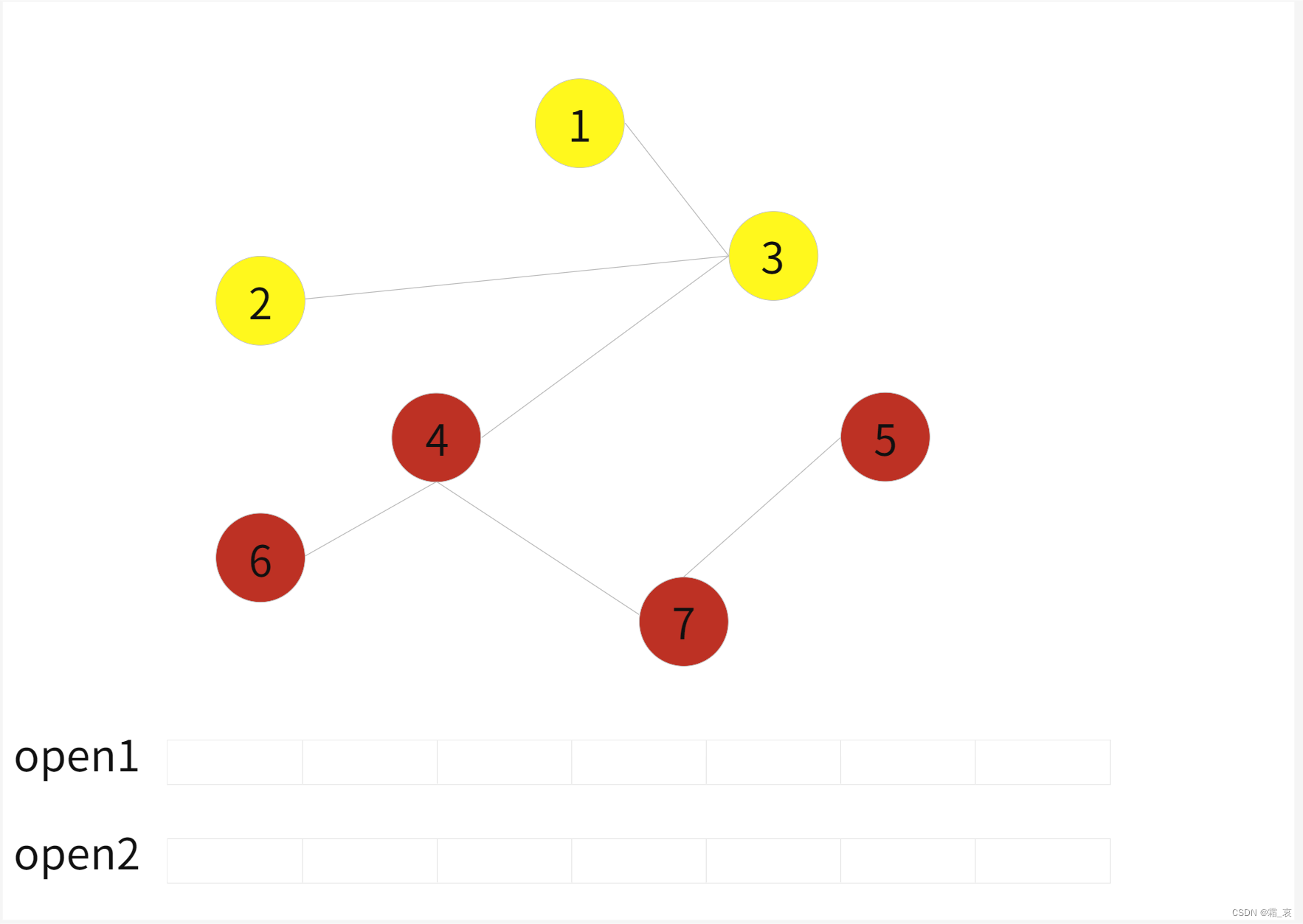
4. 又一轮搜索完成后，发现两边bfs队列都已被清空，搜索完成。（其实只需要一边队列清空就说明已经没有解了）

代码🍑

其本质就是两个bfs，但需要注意一些细节。

void double_bfs(int i,int j)
{
	op1.push_back(i);
	op2.push_back(j);
	auto x = op1.begin();
	auto y = op2.begin();
	while (1) {
		if (op1.size() == 0 || op2.size() == 0)break;
		for (int i = 1; i <= 7; i++) {
			if (G[*x][i]) {
				if (erg[i] != 0) {//erg是新维护的数组
					G[*x][i] = G[i][*x] = 0;
					break;//这里要记录下这个解的步数或者路径，就需要再维护新的东西，我就不多加了，具体问题具体新增数组或者变量就可以
				}
				op1.push_back(i);
				erg[i] = 1;
				G[*x][i] = G[i][*x] = 0;
			}
			if (G[*y][i]) {//第二部分的bfs
				if (erg[i] != 0) {
					G[*y][i] = G[i][*y] = 0;
					break;
				}
				op1.push_back(i);
				erg[i] = 2;
				G[*y][i] = G[i][*y] = 0;
			}
		}
		op1.pop_front();
		op2.pop_front();
	}
}

🍥meet in the middle🍥

原理🍩

与双向同时搜索不同，应用这个算法时我们并不知道终点状态，但我们知道一些其他的限制条件。
该算法将搜索范围从中间分为两个部分，当两个部分的搜索方案满足限制条件时，我们可以将这两个方案合并为一个解。
用一道例题来解释。

例题🍬

给定 n 个物品的价格，你有 m 块钱，每件物品限买一次，求买东西的方案数。 n≤40， m≤1018。

解析🍭

看到这个问题，很多人第一想到的是背包问题，但用背包的解法基本一定会爆时间复杂度，而普通的搜索也会爆时间复杂度，所以我们采用meet in the middle算法。
我们将n件物品分为从1到n/2和n/2+1到n两部分，然后对这两部分分别进行搜索，将搜索结果存入数组，然后当满足限制条件时，判断已满足一个解。
（两端dfs代码的模板在这里，这里我用的是排序问题的模板，由于不一定买几种东西，所以选择将r以传参的方式传入，这样看着会清晰些）

代码🍵

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int*> pur1,pur2;
int* s_val; 
int* book;
int n;
int b;
int ans = 0;
int m;
void dfs1(int num,int r)//对前半段进行搜索
{
	if (num == r) {
		int m = pur1.size();
		for (int i = 1; i <= n / 2; i++) {
			pur1[m - 1][0] = 0;
			pur1[m - 1][i] = 0;
			if (book[i] == 1)pur1[m-1][i] == 1;
			pur1[m-1][0] += s_val[i];
		}
		pur1.resize(pur1.size()+1);
		return;
	}
	for (int i = b + 1; i <= n/2; i++) {
		if (book[i] == 0) {
			b = i;
			book[i] = 1;
			dfs1(num + 1,r);
			book[i] = 0;
		}
	}
}
void dfs2(int num, int r)//对后半段进行搜索
{
	if (num == r) {
		int m = pur2.size();
		for (int i = 1; i <= n / 2; i++) {
			pur2[m - 1][0] = 0;
			pur2[m - 1][i] = 0;
			if (book[i] == 1)pur2[m - 1][i] == 1;
			pur2[m - 1][0] += s_val[i];
		}
		pur2.resize(pur2.size() + 1);
		return;
	}
	for (int i = n/2+ b + 1; i <= n; i++) {
		if (book[i] == 0) {
			b = i;
			book[i] = 1;
			dfs2(num + 1, r);
			book[i] = 0;
		}
	}
}
void ini()
{
	scanf("%d", &n);
	scanf("%d", &m);
	s_val = (int*)malloc(sizeof(int) * (n+1));
	for (int i = 1; i <= n; i++) {
		scanf("%d", &s_val[i]);
	}
	book = (int*)malloc(sizeof(int) * (n + 1));
	memset(book, 0, (n + 1) * 4);
}
int main(void)
{
	ini();
	for (int i = 1; i <= n / 2; i++) {
		dfs1(0, i);
	}
	for (int i = 1; i <= n - (n / 2); i++) {
		dfs2(0, i);
	}
	for (auto x = 1; x <=pur1.size(); x++) {
		for (auto y = 1; y <= pur2.size(); y++) {
			if (pur1[x][0] + pur2[y][0] == m)ans++;//互补条件：前后两段所花钱和为m
		}
	}
	printf("%d", ans);
	return 0;
}

总结

两端同时搜索适用于图的起点和终点都知道的题目，例如迷宫问题；而meet in the middle算法则更像是一种减小爆搜时间复杂度的技巧，它有效扩大了搜索算法支持的数据空间。

都看到这里啦，觉得还不错的同学点赞关注支持一下吧，万分感谢！！