数论---质数判断、质因子分解、质数筛（埃氏筛、欧拉筛）

阿东日志

于 2024-08-12 10:19:15 发布

阅读量345

点赞数 8

文章标签：算法开发语言 leetcode

本文链接：https://blog.csdn.net/m0_73171073/article/details/141124400

版权

如果熟悉的话直接看最后的总结进行对应算法的选择即可

质数判断、质因子分解、质数筛

质数判断

基础的判断方式

判断一个较小的质数方法

只需要验证2～n^(1/2)就可以了因为

public class Main {

    public static void main(String[] args) {

    }
    public boolean isPrime(int num){
        if (num<2) return false;

        for (int i = 0; i*i <=num; i++) {
            if (num%i==0) return false;
        }
        return true;
    }

}

所以判断一个数是不是质数时间复制度为o(n^1/2)

在判断数字较小的时候还能应对，但是数字较大时比如10^9这种时间复杂度也是O(4.5),那么要判断多个时就超时了

判断n是否为质数，Miller-Rabin测试算法

1、每次选择1～n-1范围的随机数字，或者指定一个比n小的质数，进行测试
2、测试过程中的数学原理不用纠结，不重要，因为该原理除了判断质数外不再用于其他方面
3、原理：费马小定理、Carmichael(卡米切尔数），二次探测定理、乘法同余、快速幂
4、经过s次miller-Rabin测试，s越大出错几率越低，但是速度也越慢，一般测试20次内即可

重点是用法

因为又乘法同余，所以想验证任意的long类型的数字，需要注意位数的事情

其中注意关于long类型数字的读入不要使用StramTokenizer 这个类来读取，因为

long x=(long)in.nval;这个in.nval他读取的值是double形，double在读取大数时有精度的丢失

最好使用BufferedReader这个类来进行读取一行

String s=br.readLine();

long a=Long.valueOf(s)

long类型64位置，大概是10^18次方

Miller-rabin测试算法

时间复杂度（s*logn的三次方）

使用常规的判断方式时间复杂度是(n^1/2)

//判断较大数字是否是质数（Miller-Rabin测试）
    //此时链接
    //这个代码可以解决10^9范围内的数字的质数检查
    //时间复杂度O(s*(logn)的三次方），很快，s是测试的次数
    //为什么搞不定所有的long类型（10^18次方），乘法同余时会溢出
public class Main {

    // 质数的个数代表测试的次数
    //如果如果想要增加测试的次数，那就增加更大的质数，即增加p数组的质数个数
    private static long[] p={3,5,7,11,13,17,19,23,29,31,37};
    public static boolean millerRabin(long n){
        if (n<=2) return n==2;
        if ((n&1)==0) return false;
        for (int i = 0; i < p.length && p[i]<n; i++) {
            if (witness(p[i],n)){
                return false;
            }

        }
        return true;
    }

    private static boolean witness(long a, long n) {
        long u=n-1;
        int t=0;
        while ((u&1)==0){
            t++;
            u>>=1;
        }
        long x1=power(a,u,n);
        long x2;
        for (int i = 1; i <=t ; i++) {
            x2=power(x1,2,n);
            if (x2==1&&x1!=1&&x1!=n-1){
                return true;
            }
            x1=x2;
        }
        if (x1!=1){
            return true;
        }
        return false;
    }

    //乘法同余原理
    //返回：n的p次方%mod
    //快速幂
    private static long power(long n, long p, long mod) {
        long ans=1;
        while (p>0){
            if ((p&1)==1){
                ans=(ans*n)%mod;
            }
            n=(n*n)%mod;
            p>>=1;
        }
        return ans;
    }

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String s = br.readLine();
        long a=Long.valueOf(s);
        System.out.println(millerRabin(a));

    }

}

直接使用java自带API来解决

java中对于大数其实可以直接使用BigInteger类来完成，可以存放无限大的数，其中可以直接调用isprobablePrime方法来判断一个数是否为质数，其底层也是使用Miller-Rabin测试算法完成的

题目链接

https://luogu.com.cn/problem/U148828

//使用java中的bigInteger来处理
    //可以处理任何数字
    //使用其中的isProbablePrime方法，参数只有一个，就是miller-rabin测试的次数
public class Main {

    //测试的次数
    private static int s=10;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        //判断·t个数字
        int t=Integer.valueOf(br.readLine());
        for (int i = 0; i < t; i++) {
            BigInteger n = new BigInteger(br.readLine());
            System.out.println(n.isProbablePrime(s));

        }


    }

}

小结

既然对于Miller-Rabin测试算法原理不要求，那么对于模板的记忆会比较困难，以后如果遇到判断质数的话，直接使用BigInteger这个类中的isProbablePrime算法来完成时间复杂度是s*logn的三次方

质数因子分解

是什么：就是找出一个数n的所有质数因子

方法：采用的方法是从2开始找i，然后将n一直整除i直到整除不了为止，相当于把这个数榨干，然后i++,最后如果i*i越界了并且n还！=1，那么说明当前的n就是最后一个质数因子

模板

public class Main {

    public static void main(String[] args) {
        int n=100;
        f(n);
    }
    public static void f(int n){
        for (int i = 2; i*i <=n ; i++) {
            if (n%i==0){
                System.out.println(i+" ");
                while (n%i==0){
                    n/=i;
                }
            }
        }
        if (n>1){
            System.out.println(n);
        }

    }

}

问题一：为什么直接for循环是i一直++最后i就是质数因子，这是因为我们起点是从2开始，然后只要能整除i我们就将n一直去整除i，相当于将n中的i榨干，然后才进行i++，那么比如下一个i是4,4显然不是质数，我们在判断n%4的时候一定是不成立的因为，4是2的倍数，所以i能走到4说明之前已经把2的倍数榨干了，因此这样搞完最后剩余的就是质数了

时间复杂度O(根号n)：对于整除一个数一直将这个数榨干，其时间复杂度属于常数级别，所以最终复杂度是O(n^1/2)

例题-按公因数计算最大组件大小

. - 力扣（LeetCode）

题目描述

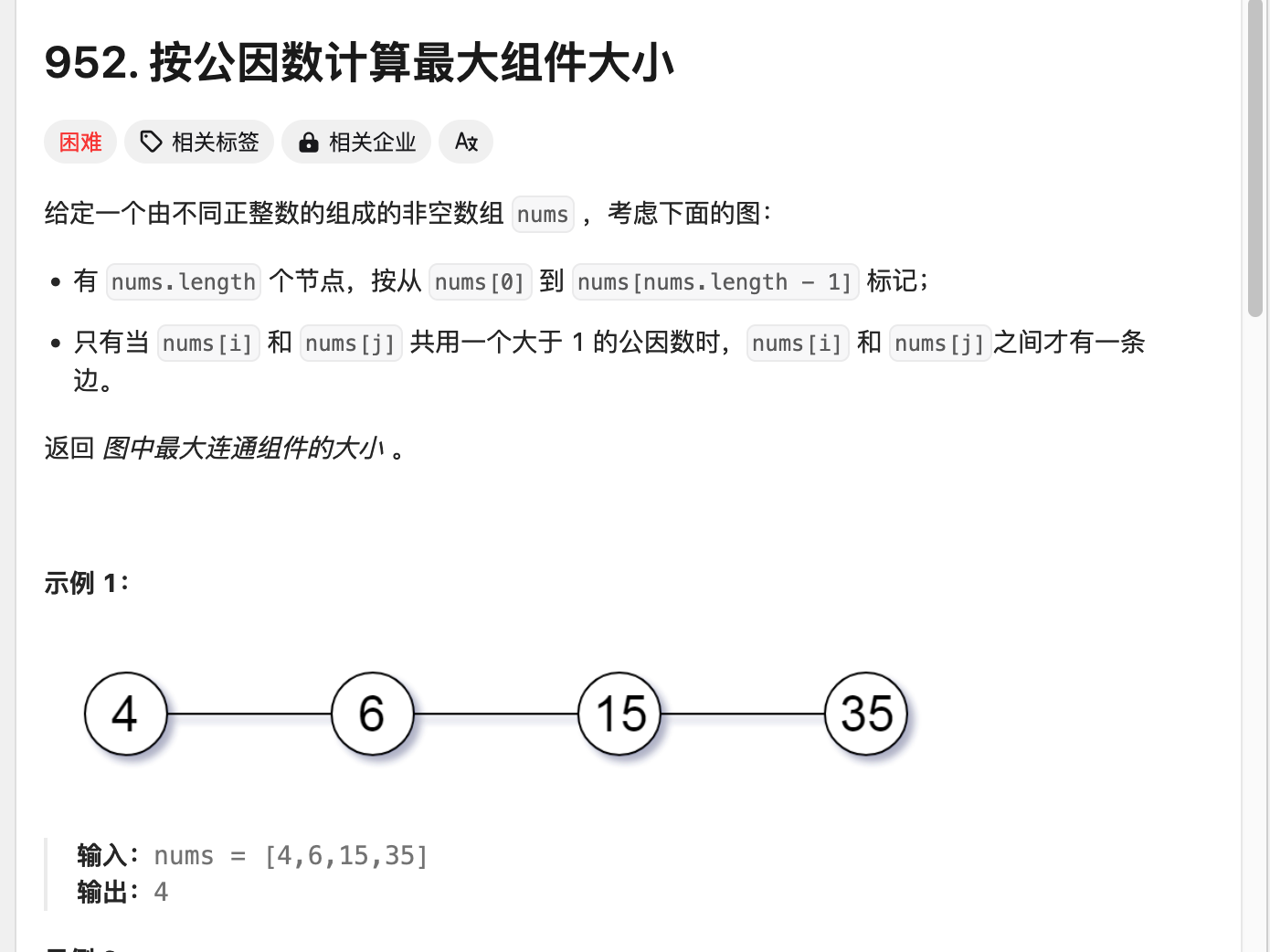
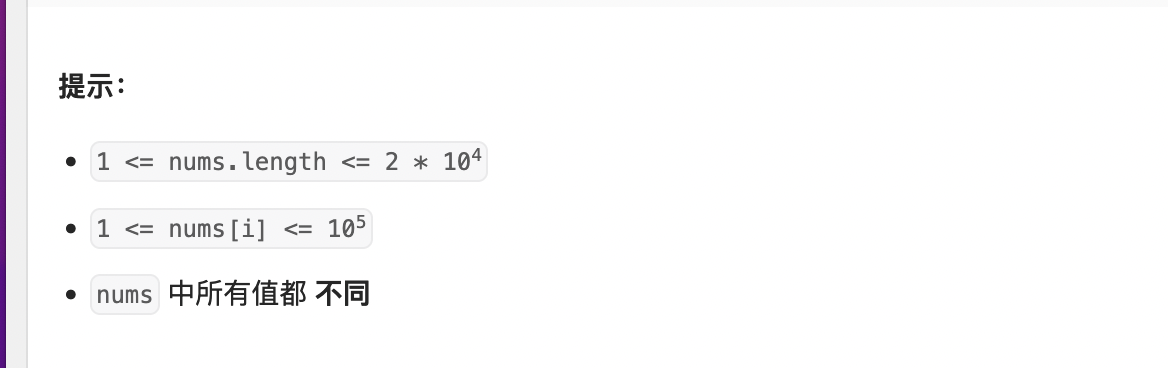
解析

看题目就是要返回数组中连通后，返回总的集合数量，一看就有一股并查集的味道，并查集做的不就是这个事情吗，这个不就是并查集所做的事情嘛，所以我们现在主要任务就是两个集合什么时候合并，从题目描述来看，两个集合合并的要求是当前数字和集合中的某个数字具有公共因子，我们不可能当前遍历到i时候还要去一个一个对比之前的数然后找到两个数的公共因子，然后合并i，j这两个数，虽然能得到结果，但是时间复杂度就上升一个维度了，所以想到用空间换时间，我们既然是通过公共质因子连接集合的，那么我们直接开辟一个数组factor[i]=x，比怕是i这个质因子第一个拥有他的是数组总的x号元素，然后遍历后面元素时分解元素质因子发现当这个质因子已经被占有了，那么我们就将这个占有元素取出来，和当前元素进行并查集

由于要返回的是集合中最大的个数，那么我们就需要再开一个数组，用来表示每个集合中的元素个数，最后返回最大

class Solution {
    //思路：
    //准备一个factor数组，factor[i]=x,表示i这个质因子已经被下标x元素占有了
    //遍历数组元素，num[i]=a,我们先去找a的值因子分解，然后看看这些质数因子是否已经被占有
    //如果之前被占有那么并查集合并两个元素集合
    //如果没有被占有说明factor[i]=-1，那么说明i因子是第一次出现，标记factor[s]=i


    private int MAXN=20001;
    private int MAXV=100010;
    private int[] father=new int[MAXN];
    //factor[i]=x:表示i这个质因子代表第一个拥有i这个质数因子的元素是下标i
    private int[] factor=new int[MAXV];
    //用来存放集合中的元素个数size[i]=x:表示以值因子关联为统一集合的元素个数为x个
    private int[] size=new int[MAXN];
    private int n=0;
    //并查集模板
    private void build(){
        for (int i = 0; i < n; i++) {
            father[i]=i;
            //一开始每个数都是一个独立集合，每个集合中有一个元素
            size[i]=1;
        }
        Arrays.fill(factor,-1);
//        Arrays.fill(size,0,n,1);
    }

    private int find(int x){
        if (father[x]!=x){
            father[x]=find(father[x]);
        }
        return father[x];
    }
    private void union(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if (fx!=fy){
            father[fy]=fx;
            //将y的个数累加到x上
            size[fx]+=size[fy];
        }
    }
    public int maxSize(){
        int ans=0;
        for (int i = 0; i <n; i++) {
            ans=Math.max(ans,size[i]);
        }
        return ans;
    }
    public int largestComponentSize(int[] nums) {
        n=nums.length;
        build();
        for (int i = 0; i < n; i++) {
            int x=nums[i];
            //质数因子分解
            for (int j = 2; j*j <=x ; j++) {
                if (x%j==0){
                    //j是x的质因子
                    if (factor[j]!=-1){
                        union(factor[j],i);
                    }else {
                        factor[j]=i;
                    }
                    while (x%j==0){
                        x/=j;
                    }
                }
            }
            if (x>1){
                //说明x分解来还剩最后x分解后的值因子
                //j是x的质因子
                if (factor[x]!=-1){
                    union(factor[x],i);
                }else {
                    factor[x]=i;
                }
            }

        }

        return maxSize();
    }
}

质数筛

是什么：给定整数n，返回1~n范围上所有的质数

埃氏筛，时间复杂O(n*log（logn)）

欧拉筛，时间复杂O(n)

其实我们掌握埃氏筛就足够了，因为时间复杂度已经非常接近线性了，而且常熟时间很不错

虽然欧拉筛的时间复杂度是O(n)但是他的常熟时间埃氏筛大常数时间可以理解为代码长度，并且欧拉筛还需要提供一个数组来存放质数集合，所以执行起来埃氏筛不一定比欧拉筛慢

埃氏筛

给定一个数组做标记

visit[i]=true:表示合数（即不是质数）

visit[i]=false:表示i是质数

算法的核心思想：

一开始我们初始化所有的位置都是质数，即都是false

然后我们从2开始筛选，我们遍历数组时发现如果当前位置不是质数即当前位置为true那么直接跳过，如果i是质数,那么我们从i*i以后每间隔i就将给位置设置为合数，以此类推最后我们遍历统计2以后false的个数就是1～n质数的个数

其实和质数分解很相似，就是当遇到质数时就将该质数的所有倍数都设置为合数就好了

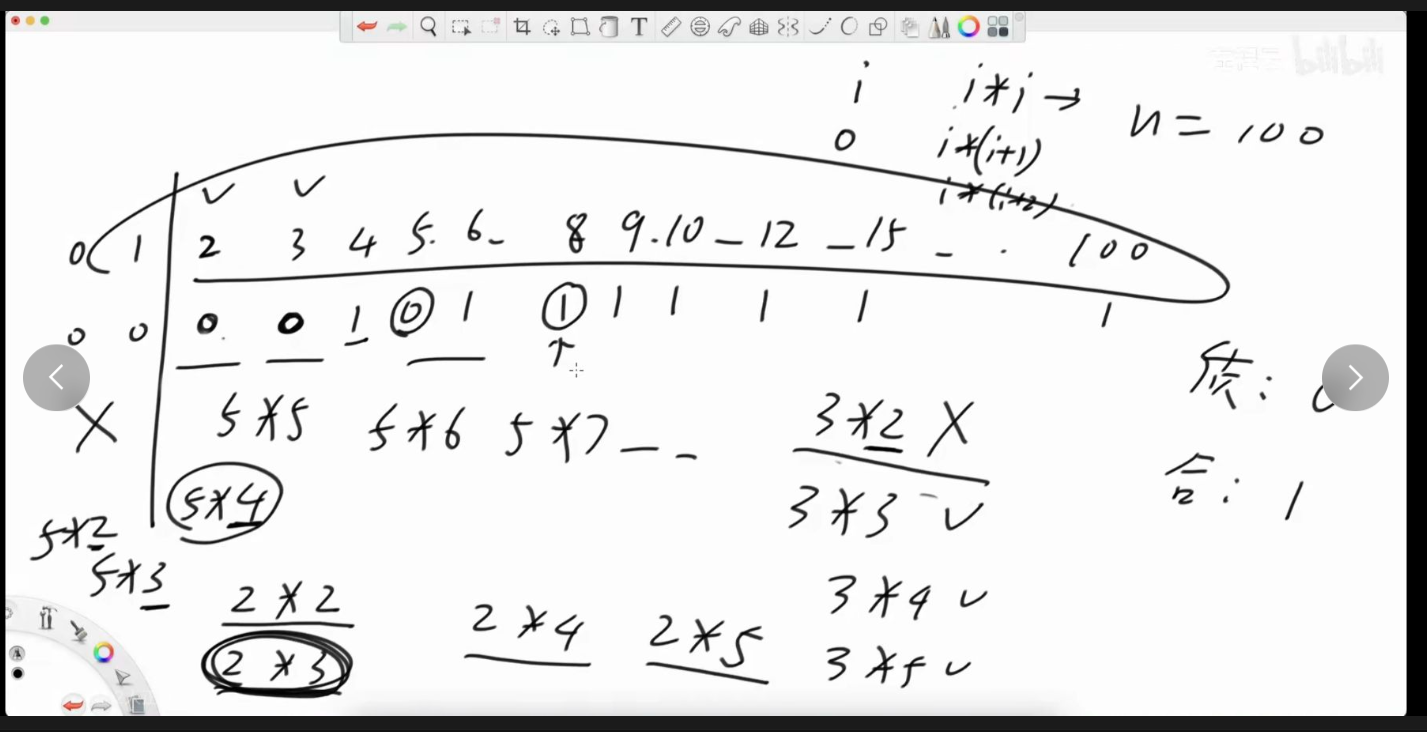
时间复杂度

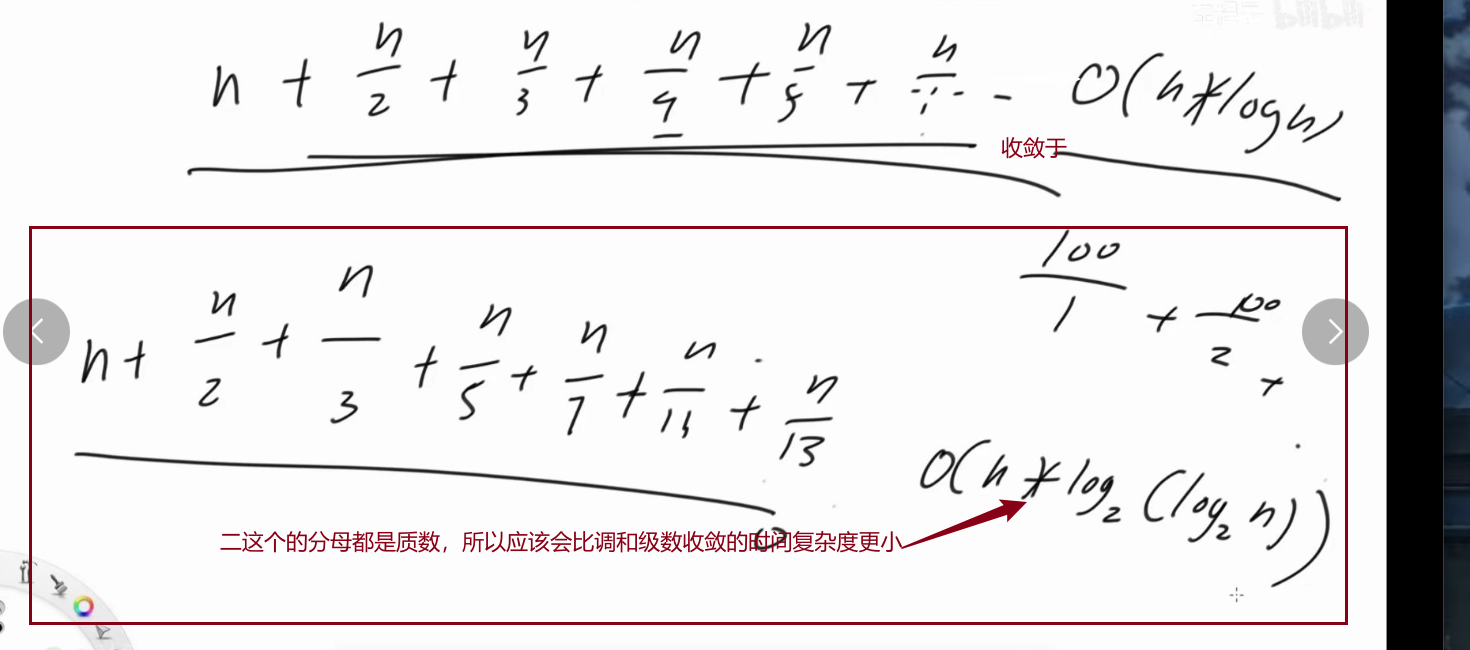
计数质数

. - 力扣（LeetCode）

题目描述

解析


class Solution {

    //首先明确为什不不直接遍历1～n使用质数判断来找到所有质数：原因就是慢，因为判断质数一个质数v是否为质数的时间复杂度为v*logv
    //就算使用miller-rabin测试判断一个数是否为质数的时间复杂度也是s*log(n)的三次方，那么判断1～n的复杂度就是n*s*（log(n)的三次方）,s为测试的次数
    //这个过不了
    //而使用埃氏筛，时间复杂度为n*log(logn))时间复杂度非常接近于线性
    //下面就是埃氏筛的过程

    public int countPrimes(int n) {

        return ehrlich(n - 1);
    }

    private int ehrlich(int n) {
        //一开始先初始化所有数字都为质数,默认都是false
        boolean[] visit = new boolean[n + 1];
        //开始筛选
        for (int i = 2; i*i <= n; i++) {
            if (!visit[i]) {
                //如果是质数，那么将后面的标记为合数
                //这里为什么直接从i*i进行设置，因为i*(i之前的数）一定已经被设置过了
                //
                for (int j = i * i; j <= n; j += i) {
                    visit[j] = true;
                }
            }
            //如果是合数直接下一个
        }
        //统计质数
        int ans = 0;
        for (int i = 2; i <= n; i++) {
            if (visit[i] == false) {
                ans++;
            }

        }
        return ans;
    }


}

注意埃氏筛的循环条件是i*i<=n这是因为我们只需i^1/2之前的数进行判断的时候就对i*i之后是不是合数进行的设置，即通过前n^1/2判断后后n^1/2就已经判断了，因为后面的数如果不是质数那么其一定含有2~n^1/2的一个因子，而前面判断质数的时候九就将i*i后面的数每次累加i设置合数已经判断了，所以这个是i*i<=n

欧拉筛

设置合数的过程

1、如果设置合数的过程超过了N那么停
2、如果没超过那么就开始以质数数组中的元素为起点乘以当前数字，来判断合数，这个可以保证合数一定是由该合数最小知数来判断的
3、如果当前数字能够整除质数数组中的某个元素，那么停止，因为我们判断合数需要的通过最小质因子来判断

例题还是计数质数


class Solution {

    public int countPrimes(int n) {

        return euler(n - 1);
    }

    //欧拉筛
    //欧拉筛其实是埃氏筛的优化版
    //因为埃氏筛的合数判断可能会被重复判断
    //而欧拉筛每个合数之后被判断一次，且这个判断只能有该合数的最小质因子来判断，一次得到只判断一次的保障
    private int euler(int n) {
        //同样认为一开始都是质数
        boolean[] visit=new boolean[n+1];
        //保存所有质数因子，1～n的质数因子个数不可能超过奇数3个数所以空间申请为n/2+1
        int[] prime=new int[n/2+1];
        int cnt=0;//统计质数集合中的个数

        //注意这里条件是i<=n而不是i*i<=n，因为不取根号n的原因我们需要利用遍历的元素来设置合数
        for (int i = 2; i<=n ; i++) {
            if (visit[i]==false){
                //是质数，加入质数集合
                prime[cnt++]=i;
            }
            //不管是不是质数，我们都使用i来结合质数数组来初始化合数
            for (int j = 0; j < cnt; j++) {
                if (i*prime[j]>n) break;
                visit[i*prime[j]]=true;
                //这个用来保证合数是由最小质数因子来判断的
                //比如合数12，一定是由2判断的
                //假设此时i=4
                //然后质数数组中一定含有2，3两个元素
                //在判断合数时，首先会设置2*4=8这个元素为合数，但是此时发现4是2的倍数，那么就直接停止通过质数数组*i判断合数了
                //因此3*4=12就不会执行，所以12就不会通过3被判断为合数，只能通过2来判断合数，这就是欧拉筛的关键，每个合数只会被1自己最小
                //质数因子判断为合数
                if (i%prime[j]==0) break;
            }

        }
        return cnt;

    }


}

需要注意的是对于欧拉筛的循环控制条件是i<=n而不是i*i<=n,和他判断和数的方式是密切相关的，对于欧拉筛，对于后面数组中一个数是合数的判断一定是由这个合数的最小质数因子判断得来的，所以为了处理这个引入了一个质数数组，然后每次判断后面的数为合数需要通过1～n的数组的数，来和质数数组相乘得到对应合数是哪一个，所以这里的循环条件就是i<=n

小结：

对于找1～n的所有质数L：

对于埃氏筛和欧拉筛如何选择其实都可以，

虽然埃氏筛时间复杂度是O(n*log(logn))但是他的常数时间少

对于欧拉筛虽然他的时间复杂度是O(n)但是他的常数时间多，且需要引入一个寸质数的数组

两者各有优缺点

对于判断质数：我这边可能只选择使用BigInteger来使用吧，反正这个类属于java8中的API笔试这种应该能使用，就不去多背起她模板了，其底层也是对于miller-Rabin测试的封装时间复杂O(s*logn的三次方）

对于质因子分解：核心思想就是从2开始找i，然后一直整除i直到把i榨干（不能再整除i了），然后再进行i++，当i*i>n了且n整除后！=1说明剩余的n就是最后一个质数

阿东日志

关注

8
点赞
踩
14

收藏

觉得还不错? 一键收藏
0
评论
数论---质数判断、质因子分解、质数筛（埃氏筛、欧拉筛）

判断一个较小的质数方法只需要验证2～n^(1/2)就可以了因为i*i <=num;i++) {所以判断一个数是不是质数时间复制度为o(n^1/2)在判断数字较小的时候还能应对，但是数字较大时比如10^9这种时间复杂度也是O(4.5),那么要判断多个时就超时了判断n是否为质数，Miller-Rabin测试算法1、每次选择1～n-1范围的随机数字，或者指定一个比n小的质数，进行测试2、测试过程中的数学原理不用纠结，不重要，因为该原理除了判断质数外不再用于其他方面。
复制链接

扫一扫