数据结构与算法分析（第2版）第一章课后练习

FlorianGo

已于 2024-04-09 15:01:18 修改

阅读量985

点赞数 37

分类专栏：数据结构算法 c语言文章标签：数据结构算法 c语言

于 2024-04-06 20:20:26 首次发布

本文链接：https://blog.csdn.net/m0_73327328/article/details/137037543

版权

数据结构同时被 3 个专栏收录

2 篇文章 0 订阅

订阅专栏

算法

2 篇文章 0 订阅

订阅专栏

c语言

2 篇文章 0 订阅

订阅专栏

前言

参考书籍：《数据结构与算法分析——C语言描述》（第2版）Mark Allen Weiss 著

学习本书需要C语言的基础，博主之前从来没有过使用C语言的经验，为此特地从零开始恶补这方面的知识T^T（当然C语言的重要性不言而喻，学习不过是迟早的事）。因此代码规范度欠佳，这里提供的答案为博主自己所编写，仅供参考，如有不妥之处还望不吝赐教！

练习1.1

实现书中所述两种低效方法：

对N元素数组进行降序冒泡排序后，返回第k个元素。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 10

void arr_init(int arr[], int size);
void bubble_sort(int arr[], int size);

int main(void)
{
    int k = N / 2;
    int arr[N];
    arr_init(arr, N);
    bubble_sort(arr, N); //降序排序
    printf("The %d-th element: %d\n", k, arr[k - 1]); //返回第k个元素

    return 0;
}

void arr_init(int arr[], int size)
{
    srand((unsigned int)time(NULL));
    for(int i = 0; i < size; i++)
    {
        arr[i] = rand();
    }
}

void bubble_sort(int arr[], int size)
{
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = 0; j < size - 1 - i; j++)
        {
            if(arr[j] < arr[j + 1])
            {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

将前k个元素读入数组并降序排序，接着将剩下元素逐个读入。读取新元素时，小于数组第k个元素则忽略，否则将其放到数组正确位置上，同时将其中一个元素（最小元素）挤出数组。最后返回数组第k个元素。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 10

void arr_init(int arr[], int size);
void arr_copy(int arr[], int k_arr[], int size);
void bubble_sort(int arr[], int size);
void arr_insert(int arr[], int size, int num);

int main(void)
{
    int k = N / 2;
    int arr[N];
    arr_init(arr, N);

    int k_arr[k];
    arr_copy(arr, k_arr, k); //将前k个元素读入新数组
    bubble_sort(k_arr, k); //降序排序

    for(int i = k; i < N; i++) //将剩下元素逐个读入
    {
        if (arr[i] < k_arr[k - 1]) //小于数组中第k个元素则忽略
            continue;
        arr_insert(k_arr, k, arr[i]); //放到正确的位置上
    }

    printf("The %d-th element: %d\n", k, k_arr[k - 1]); //返回第k个元素

    return 0;
}

void arr_init(int arr[], int size)
{
    srand((unsigned int)time(NULL));
    for(int i = 0; i < size; i++)
    {
        arr[i] = rand();
    }
}

void arr_copy(int arr[], int k_arr[], int size)
{
    for(int i = 0; i < size; i++)
    {
        k_arr[i] = arr[i];
    }
}

void bubble_sort(int arr[], int size)
{
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = 0; j < size - 1 - i; j++)
        {
            if(arr[j] < arr[j + 1])
            {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

void arr_insert(int arr[], int size, int num)
{
    for(int i = 0; i < size; i++)
    {
        if(arr[i] < num)
        {
            for(int j = size - 1; j > i; j--) //将最小元素挤出数组
            {
                arr[j] = arr[j - 1];
            }
            arr[i] = num;
            break;
        }
    }
}

练习1.2

字谜问题游戏：

对单词表中的每个单词，检查每个有序三元组（行，列，方向），验证是否有单词存在。

#include <stdio.h>
#include <string.h>
#define ROWS 4
#define COLUMNS 4

enum direction
{
    x0y0, //0，x--，y--
    x0y1, //1，x--，y=y
    x0y2, //2，x--，y++
    x1y0, //3，x=x，y--
    x1y1, //4，x=x，y=y，无意义，占位用
    x1y2, //5，x=x，y++
    x2y0, //6，x++，y--
    x2y1, //7，x++，y=y
    x2y2 //8，x++，y++
};

void Check(const char * words[4], const char table[ROWS][COLUMNS], int start_x, int start_y, enum direction dir);

int main(void)
{
    const char * words[4] ={ "this", "two", "fat", "that" };
    const char table[ROWS][COLUMNS] =
    {
        { 't', 'h', 'i', 's' },
        { 'w', 'a', 't', 's' },
        { 'o', 'a', 'h', 'g' },
        { 'f', 'g', 'd', 't' }
    };

    for(int x = 0; x < ROWS; x++)
    {
        for(int y = 0; y < COLUMNS; y++)
        {
            for(int dir = 0; dir < 9; dir++)
                Check(words, table, x, y, dir); //有序三元组（行，列，方向）
        }
    }

    return 0;
}

void Check(const char * words[4], const char table[ROWS][COLUMNS], int start_x, int start_y, enum direction dir)
{
    //xy不变化，无意义
    if(dir == x1y1)
        return;

    int dir_x = dir / 3 - 1; //x轴方向（根据二维数组特性向下）
    int dir_y = dir % 3 - 1; //y轴方向（根据二维数组特性向右）

    char temp[10] = ""; //创建临时空字符
    int strIndex = 0; //逐字符存入
    int end_x = start_x; //临时字符串终止位置x
    int end_y = start_y; //临时字符串终止位置y

    while(end_x >= 0 && end_x < ROWS && end_y >= 0 && end_y < COLUMNS)
    {
        //向temp添加字符
        temp[strIndex++] = table[end_x][end_y];
        temp[strIndex] = '\0';

        //将temp依次与单词表对照
        for(int i = 0; i < 4; i++)
        {
            if(strcmp(words[i], temp) == 0)
                printf("%s from (%d, %d) to (%d, %d)\n", temp, start_x+1, start_y+1, end_x+1, end_y+1); //显示字符串及起始终止位置
        }
        
        //更新字符串终止位置
        end_x += dir_x;
        end_y += dir_y;
    }
}

对于每一个尚未进行到字谜最后的有序四元组（行，列，方向，字符数）测试所指的单词是否在单词表中。

#include <stdio.h>
#include <string.h>
#define ROWS 4
#define COLUMNS 4

enum direction
{
    x0y0, //0，x--，y--
    x0y1, //1，x--，y=y
    x0y2, //2，x--，y++
    x1y0, //3，x=x，y--
    x1y1, //4，x=x，y=y，无意义，占位用
    x1y2, //5，x=x，y++
    x2y0, //6，x++，y--
    x2y1, //7，x++，y=y
    x2y2 //8，x++，y++
};

void Check(const char * words[4], const char table[ROWS][COLUMNS], int start_x, int start_y, enum direction dir, int length);

int main(void)
{
    const char * words[4] ={ "this", "two", "fat", "that" };
    const char table[ROWS][COLUMNS] =
    {
        { 't', 'h', 'i', 's' },
        { 'w', 'a', 't', 's' },
        { 'o', 'a', 'h', 'g' },
        { 'f', 'g', 'd', 't' }
    };

    for(int x = 0; x < ROWS; x++)
    {
        for(int y = 0; y < COLUMNS; y++)
        {
            for(int dir = 0; dir < 9; dir++)
            {
                for(int i = 1; i <= ROWS || i <= COLUMNS; i++)
                {
                    Check(words, table, x, y, dir, i); //有序四元组（行，列，方向，字符数）
                }
            }
        }
    }

    return 0;
}

void Check(const char * words[4], const char table[ROWS][COLUMNS], int start_x, int start_y, enum direction dir, int length)
{
    //xy不变化，无意义
    if(dir == x1y1)
        return;

    int dir_x = dir / 3 - 1; //x轴方向（根据二维数组特性向下）
    int dir_y = dir % 3 - 1; //y轴方向（根据二维数组特性向右）

    //超出表格范围
    if (start_x + dir_x * (length-1) < 0 || start_x + dir_x * (length-1) >= ROWS || start_y + dir_y * (length-1) < 0 || start_y + dir_y * (length-1) >= COLUMNS)
        return;

    //长度为length的对照字符串temp
    char temp[length+1]; //对于不支持变长数组的编译器可以使用常数量
    for(int i = 0; i < length; i++)
    {
        temp[i] = table[start_x + dir_x * i][start_y + dir_y * i];
    }
    temp[length] = '\0';

    //将temp依次与单词表对照
    for(int i = 0; i < 4; i++)
    {
        if(strcmp(words[i], temp) == 0)
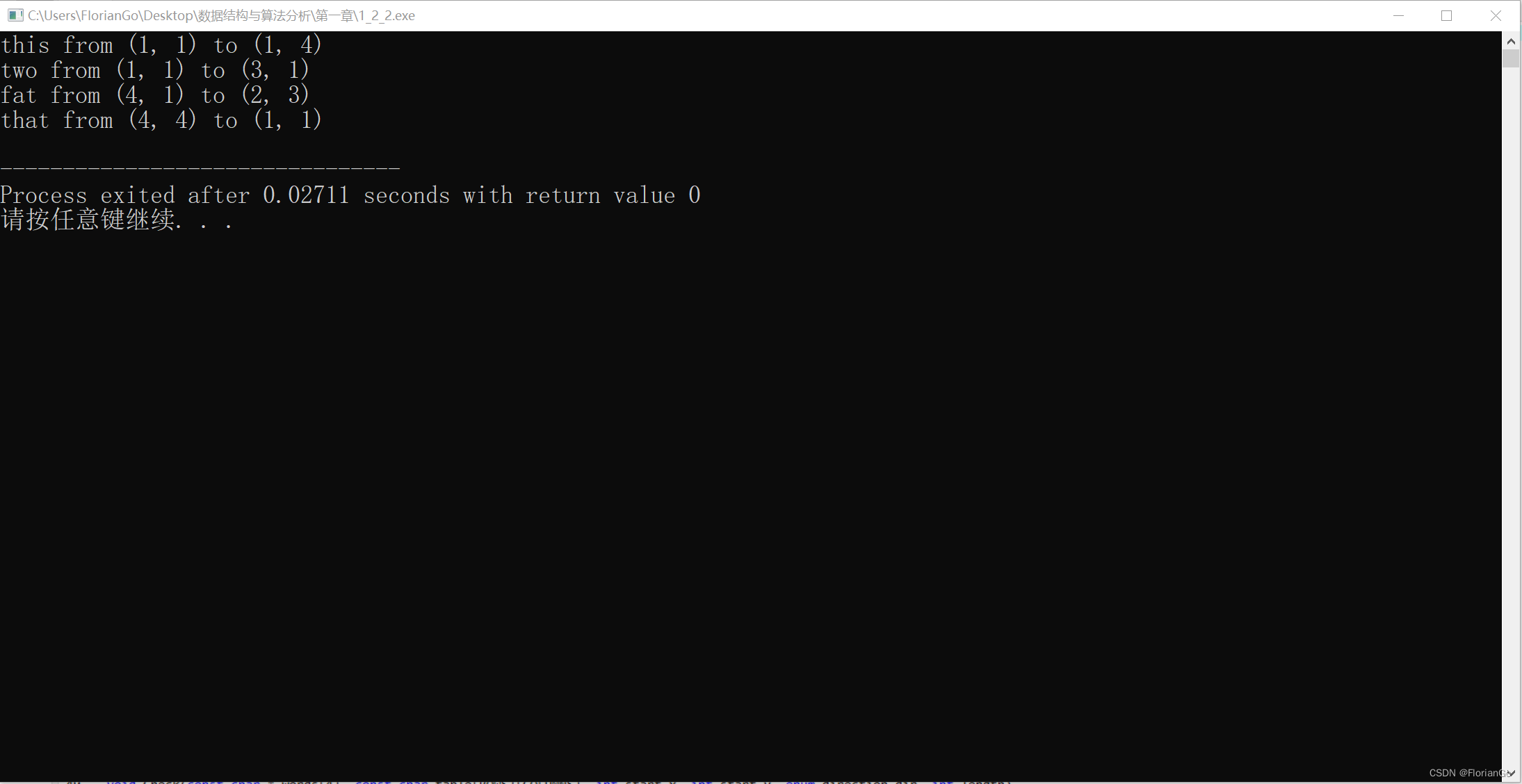
            printf("%s from (%d, %d) to (%d, %d)\n", temp, start_x+1, start_y+1, start_x + dir_x * (length-1) + 1, start_y + dir_y * (length-1) + 1); //显示字符串及起始终止位置
    }
}

结果如下：

练习1.3

这里不太能够理解题目的意思，只能想象到以小数点为分界线分别递归打印整数与小数部分，通过特殊条件显式控制 PrintDigit 函数打印负号 " - " 与小数点 " . " ，~~下面的代码看看就好了~~

#include <stdio.h>
#include <stdbool.h>

void PrintOut(double N);
void PrintInteger(long N);
void PrintFraction(double N);
void PrintDigit(long N, bool print_symbol);

int main(void)
{
    PrintOut(-86420.013579);

    return 0;
}

void PrintOut(double N) //打印实数
{
    if(N < 0) //负数则打印负号并转化为正数
    {
        PrintDigit(N, true); //传入负数打印负号
        N = -N;
    }

    PrintInteger(N); //递归打印整数部分
    if(N - (long)N) //如果存在小数部分
    {
        PrintDigit(0, true); //打印小数点
        PrintFraction(N - (long)N); //递归打印小数部分
    }
}

void PrintInteger(long N)
{
    if(N >= 10)
        PrintInteger(N / 10);
    PrintDigit(N % 10, false);
}

void PrintFraction(double N)
{
    N *= 10.0; //小数点后移一位
    if(N > 0.01)
    {
        PrintDigit(N, false); //每次打印一位（整数部分）
        PrintFraction(N - (long)N); //递归
    }
}

void PrintDigit(long N, bool print_symbol)
{
    if(N >= 10) //检查确保每次打印一位数
        puts("Error");
    if(print_symbol) //打印特殊符号
        fputs(N < 0 ? "-" : ".", stdout);
    else //打印单个数字
        printf("%d", (long)N);
}

练习1.4

读入被 include 语句修饰的一个文件并输出这个文件：

由于缺乏相关经验，这里我使用了一种最简单粗暴的方法，以文本模式读取当前文件并寻找 #include "_filename" 修饰内容，再通过该文件名打开该文件输出到控制台上。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "1_4_test.h"

int main(void)
{
    char target_file_name[100] = ""; //目标打开文件名
    FILE * target_file; //目标打开文件

    FILE * current_file = fopen(__FILE__, "r"); //当前文件
    char cmp_text[8]; //寻找"include"字符串
    char ch; //临时存储字符
    while((ch = getc(current_file)) != EOF) //循环读取文件
    {
        if(ch == '#') //预处理指令，检查是否为"include"
            fgets(cmp_text, 8, current_file);
        if(strcmp(cmp_text, "include") == 0)
        {
            cmp_text[0] = '\0'; //清空字符串

            while((ch = getc(current_file)) != '"') //找到第一个双引号
            {
                if(ch == '<') //标准库文件（不是我们想找的）
                    break;
                continue;
            }
            if(ch != '"') //只找双引号内的文件
                continue;

            int index = 0;
            while((ch = getc(current_file)) != '"') //读取文件名，到第二个双引号为止
            {
                target_file_name[index++] = ch;
            }
            target_file_name[index] = '\0';
        }
    }

    if((target_file = fopen(target_file_name, "r")) == NULL) //尝试打开文件
    {
        printf("Cannot open the file.");
        exit(EXIT_FAILURE);
    }
    //成功读取文件
    printf("\nReading %s ...\n\n", target_file_name);
    while((ch = getc(target_file)) != EOF) //输出目标文件
    {
        putc(ch, stdout);
    }
    fputs("\n\nRead complete.\n", stdout);

    return 0;
}

练习1.5

（a）求证：logX < X 对所有的 X > 0 成立

证明：

问题转化：

对 X > 0：

0 < logX < X

<=> 2 ^ (logX) < 2 ^ X

<=> X < 2 ^ X

<=> 2 ^ X - X > 0

考虑 f(X) = 2 ^ X - X :

f(X)'' = ln(4) * (2 ^ X) > 0

=> f(X)为凸函数（convex），存在且仅存在一个全局最小值

f(X)' = ln(2) * (2 ^ X) - 1 = 0

=> 当且仅当 X = log(1 / ln(2)) = -log(ln(2)) ≈ 0.53 时，f(X)取全局最小值 f(X)min

当 X = -log(ln(2)) 时，

f(X) = f(X)min = 1 / ln(2) + log(ln(2)) ≈ 0.91 > 0

∴ f(X) >= f(X)min > 0, X ∈ R

=> f(X) = 2 ^ X - X > 0, X ∈ (0,+∞)

∴ logX < X 对所有的 X > 0 成立

证毕

（b）求证：log(A ^ B) = B * log(A)

证明：

根据指数基本公式：

(X ^ A) ^ B = X ^ (A * B)

(2 ^ log(A)) ^ B = 2 ^ (log(A) * B)

log((2 ^ log(A)) ^ B) = log(2 ^ (log(A) * B))

log(A ^ B) = log(A) * B = B * log(A)

证毕

练习1.6

求和：

（a）Σ(1 / 4^i)

设 Σ(1 / 4^i) = S

= 1/1 + 1/4 + 1/16 + ... + lim[i→∞](1 / 4^i)，

则 (1/4) * S = Σ(1 / 4^(i+1))

= 1/4 + 1/16 + 1/64 + ... + lim[i→∞](1 / 4^i) + lim[i→∞](1 / 4^(i+1))。

S - (1/4) * S = (3/4) *S

= 1 - lim[i→∞](1 / 4^(i+1))

= 1 - 0 = 1

∴ Σ(1 / 4^i) = S = 4/3

（b）Σ(i / 4^i)

设 Σ(i / 4^i) = S

= 0/1 + 1/4 + 2/16 + ... + lim[i→∞](i / 4^i)，

则 (1/4) * S = Σ(i / 4^(i+1))

= 0/4 + 1/16 + 2/64 + ... + lim[i→∞]((i-1) / 4^i) + lim[i→∞](i / 4^(i+1))。

S - (1/4) * S = (3/4) *S

= 1/4 + 1/16 + ... + lim[i→∞](1 / 4^i) - lim[i→∞](i / 4^(i+1))

= Σ(1 / 4^(i+1)) - 0

= (1/4) * Σ(1 / 4^i)

= (1/4) * (4/3) = 1/3

∴ Σ(i / 4^i) = S = 4/9

（*c）Σ(i² / 4^i)

利用微分法求解：

对于 q ∈ (0,1)，

Σ(q^i) = 1 + q + q² + q³ + ... = 1 / (1 - q)

两边同时对q求导：

(Σ(q^i))' = 0 + 1 + 2q + 3q² + ... = 1 / (1 - q)²

=>

Σ(i * q^i) = 0 + 1q + 2q² + 3q³ + ...

= q * (Σ(q^i))' = q / (1 - q)²

两边同时对q求导：

(Σ(i * q^i))' = 0 + 1² + 2²q + 3²q² + ... = 1 / (1 - q)² + 2q / (1 - q)³

=>

Σ(i² * q^i) = 0 + 1²q + 2²q² + 3²q³ + ...

= q * (Σ(i * q^i))' = q / (1 - q)² + 2q² / (1 - q)³

代入 q = 1/4：

Σ(i² * (1/4)^i)

= (1/4) / (1 - 1/4)² + 2 * (1/4)² / (1 - 1/4)³

= 20/27

∴ Σ(i² / 4^i) = Σ(i² * (1/4)^i) = 20/27

（**d）Σ(i^N / 4^i)

由（c）中步骤可推断：

Σ(i^N * q^i) = q * (Σ(i^(N-1) * q^i))'

即

Σ(i^N * q^i) = q * (q * ( ... (q * (Σ(q^i))')' ... )')'

... ... // 通项式没整出来-_-||

练习1.7

估计Σ[i=N/2,N](1 / i)

设 2 ^ n <= N < 2 ^ (n + 1)，

则 log(N) - 1 < n <= log(N)。

Σ[i=1,N](1 / i) = 1 + 1/2 + 1/3 + ... + 1/N

< 1 + (1/2 + 1/2) + (1/4 + 1/4 + 1/4 + 1/4) + ... + (1/(2^n) + 1/(2^n) + ... + 1/(2^n))

<= n <= log(N)

// 这里我偷懒跳步了，意会一下哈

lim[N→∞](Σ[i=1,N](1 / i)) = lim[N→∞](log(N))

∴ Σ[i=N/2,N](1 / i)

= Σ[i=1,N](1 / i) - Σ[i=1,N/2 - 1](1 / i)

≈ log(N) - log(N/2 - 1) ≈ log(N) - log(N/2) = 1

即 Σ[i=N/2,N](1 / i) ≈ 1

*练习1.8

(2 ^ 100) mod 5 是多少？

参考定理：

(A ^ B) mod C = (A mod C) ^ (B mod Φ(C))

解释：

Φ(n)，欧拉函数(Euler's totient function)，表示所有小于等于n且与n互质的数的个数

5是质数 => Φ(5) = 4

(2 ^ 100) mod 5

= (2 mod 5) ^ (100 mod 4)

= 2 ^ 0

= 1

练习1.9

斐波那契数列：F(0) = 1，F(1) = 1，F(2) = 2，F(3) = 3，F(4) = 5，... ，F(i) = F(i-1) + F(i-2)

（a）求证：Σ[i=1,N-2](F(i)) = F(N) - 2

（通过数学归纳法）证明：

（i）当N = 3，Σ[i=1,3-2](F(i)) = F(1) = F(3) - 2，命题成立。

（ii）假设对于任意N >= 3，满足命题 Σ[i=1,N-2](F(i)) = F(N) - 2。

（iii）则对于N+1：

左式 = Σ[i=1,N+1-2](F(i)) = Σ[i=1,N-2](F(i)) + F(N-1)

右式 = F(N+1) - 2 = F(N) - 2 + F(N-1)

∵ Σ[i=1,N-2](F(i)) = F(N) - 2

∴ Σ[i=1,N-2](F(i)) + F(N-1) = F(N) - 2 + F(N-1)

即左式 = 右式，命题成立。

由（i）、（ii）、（iii）可得 Σ[i=1,N-2](F(i)) = F(N) - 2 对于任意N >= 3成立。

证毕

（b）求证：F(N) < Φ ^ N，其中 Φ = (1 + 5^(1/2)) / 2

（通过数学归纳法）证明：

（i）当N = 1，F(1) = 1 < Φ，命题成立；

当N = 2，F(2) = 2 < Φ²，命题成立。

（ii）假设对于任意N >= 1，满足命题 F(N) < Φ ^ N 与 F(N+1) < Φ ^ (N+1)。

（iii）则对于N+2：

F(N+2) = F(N+1) + F(N) < Φ ^ N + Φ ^ (N+1) = Φ ^ N * (1 + Φ)

∵ 1 + Φ - Φ² = 0 => 1 + Φ = Φ²

∴ F(N+2) < Φ ^ N * Φ² = Φ ^ (N+2)

命题成立。

由（i）、（ii）、（iii）可得 F(N) < Φ ^ N 对于任意N >= 1成立。

证毕

（**c）给出F(N)封闭形式的准确表达式

假设存在 等比数列A(N) = a ^ N 与 B(N) = b ^ N 满足斐波那契数列性质，

即 A(N+2) = A(N+1) + A(N)，B(N+2) = B(N+1) + B(N)。

=>

(a ^ N) * a² = (a ^ N) * a + (a ^ N)

(b ^ N) * b² = (b ^ N) * b + (b ^ N)

=>

(a ^ N) * (a² - a - 1) = 0

(b ^ N) * (b² - b - 1) = 0

=>

a = (1 + 5^(1/2)) / 2

b = (1 - 5^(1/2)) / 2

设 F(N) = c1 * (a ^ N) + c2 * (b ^ N)（c1，c2为常数），易证该式满足斐波那契数列性质。

代入前两项：

F(0) = c1 * (a ^ 0) + c2 * (b ^ 0)

F(1) = c1 * (a ^ 1) + c2 * (b ^ 1)

=>

c1 = 5 ^ (-1/2) * (1 + 5^(1/2)) / 2 = 5 ^ (-1/2) * a

c2 = -5 ^ (-1/2) * (1 - 5^(1/2)) / 2 = -5 ^ (-1/2) * b

∴ F(N) = 5 ^ (-1/2) * ((1 + 5^(1/2)) / 2) ^ (N+1) - 5 ^ (-1/2) * ((1 - 5^(1/2)) / 2) ^ (N+1)

练习1.10

（a）求证：Σ[i=1,N](2i-1) = N²

证明：

根据求和公式：Σ[i=1,N](i) = (N * (N+1)) / 2

Σ[i=1,N](2i-1)

= 2 * Σ[i=1,N](i) - Σ[i=1,N](1)

= 2 * ((N * (N+1)) / 2) - N

= N² + N - N = N²

证毕

（b）求证：Σ[i=1,N](i³) = (Σ[i=1,N](i))²

证明：

(n + 1)² - n² = 2n + 1

n² - (n - 1)² = 2(n - 1) + 1

...

2² - 1² = 2*1 + 1

=>

(n + 1)² - 1² = 2 * Σ[i=1,N](i) + Σ[i=1,N](1)

n² + 2n = 2 * Σ[i=1,N](i) + n

∴ Σ[i=1,N](i) = (n² + n) / 2 = n(n+1) / 2

(n + 1)³ - n³ = 3n² + 3n + 1

n³ - (n - 1)³ = 3(n - 1)² + 3(n - 1) + 1

...

2³ - 1³ = 3*1² + 3*1 + 1

=>

(n + 1)³ - 1³ = 3 * Σ[i=1,N](i²) + 3 * Σ[i=1,N](i) + Σ[i=1,N](1)

n³ + 3n² + 3n = 3 * Σ[i=1,N](i²) + 3 * (n(n+1) / 2) + n

∴ Σ[i=1,N](i²) = (2n³ + 6n² + n) / 6 = n(n+1)(2n+1) / 6

(n + 1)⁴ - n⁴ = 4n³ + 6n² + 4n + 1

n⁴ - (n - 1)⁴ = 4(n - 1)³ + 6(n - 1)² + 4(n - 1) + 1

...

2⁴ - 1⁴ = 4*1³ + 6*1² + 4*1 + 1

=>

(n + 1)⁴ - 1⁴ = 4 * Σ[i=1,N](i³) + 6 * Σ[i=1,N](i²) + 4 * Σ[i=1,N](i) + Σ[i=1,N](1)

n⁴ + 4n³ + 6n² + 4n = 4 * Σ[i=1,N](i³) + 6 * (n(n+1)(2n+1) / 6) + 3 * (n(n+1) / 2) + n

∴ Σ[i=1,N](i³) = (n⁴ + 2n³ + n²) / 4 = n²(n+1)² / 4

即 Σ[i=1,N](i³) = (Σ[i=1,N](i))²

证毕

上述（b）小题也可以通过数学归纳法证明

FlorianGo

关注

37
点赞
踩
22

收藏

觉得还不错? 一键收藏
1
评论
数据结构与算法分析（第2版）第一章课后练习

数据结构与算法分析——C语言描述》（第2版）Mark Allen Weiss 著学习本书需要C语言的基础，博主之前从来没有过使用C语言的经验，为此特地从零开始恶补这方面的知识T^T（当然C语言的重要性不言而喻，学习不过是迟早的事）。因此代码规范度欠佳，这里提供的答案为博主自己所编写，仅供参考，如有不妥之处还望不吝赐教！
复制链接

扫一扫