【复杂网络分析-图的基本属性和参数计算】

前言

        本文讲解了网络的基本定义，同时介绍了网络的基本属性，例如边的源节点，目标节点和权重，以及节点的中心性属性，例如度中心性、中介中心性、接近中心性以及特征向量中心性，同时介绍了网络的全局属性，例如网络密度、度分布、平均最短路径和全局聚类系数。

一、图(网络)是什么？

        图由节点（node）和连接它们的边（edge）构成。节点代表网络中的实体或个体，可以是人、计算机、路由器等。边则表示节点之间的关系或连接，可以是通信链路、社交关系、数据传输等。

        在图论中，图可以分为有向图和无向图两种类型，它们之间的主要区别在于边的方向性。

        无向图（Undirected Graph）：其中边没有方向，即连接两个节点的边是没有箭头的。在无向图中，边是双向的，表示两个节点之间的对等关系。例如，社交网络中的朋友关系可以用无向图来表示，因为朋友关系是相互的，没有明确的方向。

        有向图（Directed Graph）：其中边有方向，即连接两个节点的边有箭头指向其中一个节点。在有向图中，边是单向的，表示两个节点之间的单向关系。例如，互联网中的网页链接关系可以用有向图来表示，因为网页之间的链接是单向的，一个网页可以链接到另一个网页，但反过来不一定有链接。下图展示了一个简单的图，其中左边是无向图，右边是有向图。

二、图的基本属性

(一)边属性

        1.源节点与目标节点

        在图论中，边的源节点（source node）是指连接边的起始节点或起点。在有向图中，边有明确的方向，其中一个节点作为边的起始点，称为源节点；另一个节点作为边的终点，称为目标节点（target node）

        2.边的权重

        在图中，边的权重是指连接两个节点的边的相关值或度量。它可以表示不同类型的关系强度、距离、成本等。边的权重可以是实数、整数或其他类型的值，具体取决于应用场景和问题的需求。

        下面是一个简单的例子来说明边的权重：

        考虑一个无向图，表示城市之间的道路网络。每条道路都有一个长度作为权重，表示两个城市之间的距离。假设有三个城市 A、B 和 C，它们之间的道路连接如下：

• A 和 B 之间的道路长度为 5 单位。
• B 和 C 之间的道路长度为 3 单位。
• A 和 C 之间没有直接的道路连接。

        在这个例子中，边的权重表示了两个城市之间的距离。例如，A 和 B 之间的边的权重为 5，表示 A 和 B 之间的距离为 5 单位。

        边的权重在图论中非常重要，它可以用于计算最短路径、最小生成树、网络流等各种图算法和分析中。通过给边赋予不同的权重，可以更好地描述和分析节点之间的关系和连接特征。

(二)节点属性

        1.节点权重

        节点的权重属性表示节点的重要性或价值。在一些图算法中，节点的权重可以影响算法的结果。

        2.出度/入度

        出度是指从一个节点发出的边的数量，即从该节点指向其他节点的边的数量。出度表示了一个节点向外部节点的连接强度或流出的关系。

        对于下图的节点X来说，indegree表示入度,outdegree表示出度，其中X节点的入度为5，表示有5条边指向X节点，X的出度为也为5，表示X节点指出了5条边到其他的节点。对于无向图而言，出度和入度是相等的，因此没有出度和入度的概念。无向图只有度这个属性。

3.中心性

        节点的中心性（Centrality）是用来衡量图中节点在网络结构中的重要性或中心位置的指标。不同的中心性指标可以衡量节点在网络中的不同方面的重要性，比如节点在信息传播、网络连通性、影响力等方面的作用程度。节点中心性有许多不同的计量方法。

        度中心性（Degree Centrality）：

        度中心性衡量节点的度，即与该节点相连的边的数量。度中心性高的节点通常在网络中具有更多的连接，可能在信息传播和网络流动性方面起着重要作用。

        通常，为了便于比较或进行其他计算，需要对度中心度进行标准化处理。标准化的方式通常是将每个顶点的度除以图中可能的最大度数，即N-1，其中N代表图中的顶点总数。

        中介中心性 （Betweenness centrality）

        网络中两个非相邻成员之间的相互作用依赖于其他成员，特别是两成员之间路径上的那些成员。他们对两个非相邻成员之间的相互作用具有控制和制约作用。Freeman (1979)认为中间成员对路径两端的成员具有“更大的人际关系影响”。因此，中介中心性的思想是：如果一个成员位于其他成员的多条最短路径上，那么该成员就是核心成员，就具有较大的中介中心性。

        举个例子：假设有一个社交达人，他认识了 Alice、Bob、Cathy 和 Dave 四个人。Alice、Bob、Cathy 和 Dave 之间也相互认识。现在，如果有人想要通过最短路径从 Alice 到 Bob，可能会经过这个社交达人。同样，如果有人想要通过最短路径从 Cathy 到 Dave，也会经过这个社交达人。这个社交达人在连接其他人之间的最短路径中扮演了重要的桥梁角色，因此他的中介中心性就很高。

        中介中心性指的是一个结点担任其它两个结点之间最短路的桥梁的次数。一个结点充当“中介”的次数越高，它的中介中心度就越大。如果要考虑标准化的问题，可以用一个结点承担最短路桥梁的次数除以所有的路径数量。

        接近中心性 （Closeness centrality）

        接近中心性（Closeness Centrality）是网络分析中用来衡量一个节点到其他节点的平均最短路径长度的指标。通俗地说，接近中心性可以帮助我们了解一个节点与其他节点之间有多“近”，也就是说，一个节点到其他节点的距离有多短。

        想象一下，有一个社交网络，其中每个人都是一个节点，而他们之间的关系就是网络中的边。接近中心性就像是在衡量一个人和其他人之间的“距离”。如果一个人的接近中心性很高，意味着他与其他人之间的平均距离很短，也就是说，他与其他人之间的联系比较紧密。

        特征向量中心性（eigenvector centrality）

        特征向量中心性可以简单理解为一个节点的重要程度取决于它连接的其他重要节点有多少。如果一个节点连接的节点都很重要，那么这个节点本身也会被认为很重要。

        举个例子，假设有一个社交网络，其中A、B、C三个人互相之间有联系。如果A和B是社交网络中最受欢迎的人，他们的特征向量中心性会很高。而如果C只与A和B有联系，那么虽然C本身可能并不是很重要，但由于它与A、B这两个重要节点有联系，C的特征向量中心性也会相对较高。

        特征向量中心性可以帮助我们找出在网络中具有重要影响力的节点，例如在社交网络中找到关键的意见领袖，或者在网页链接网络中找到最重要的网页。这有助于我们更好地理解网络结构和改进网络的性能。

        谷歌的PageRank和Katz中心度是特征向量中心度的变种。在计算特征向量中心性时，通常需要给节点一个初始的重要程度值。这个初始值可以是随机分配的，也可以是根据节点的某些属性或者其他指标来确定的。

4.节点聚类系数(局部聚类系数)

        节点的聚类系数是指该节点的邻居节点之间形成连接的概率。聚类系数可以反映节点所在的社区结构和节点之间的紧密程度。

        1.对于一个节点i，假设它有ki个邻居节点（即与节点i直接相连的节点数）。

        2.计算节点i的邻居节点之间的实际边数Ei和可能的边数ki * (ki - 1) / 2。

        3.节点i的聚类系数Ci定义为实际边数Ei与可能的边数ki * (ki - 1) / 2 之比，即 Ci = 2 * Ei / (ki * (ki - 1))。

        举例说明：
        假设节点i有3个邻居节点，分别为A、B、C，那么节点i的邻居节点之间的连接情况如下： 

•  A和C相连​​​​​​
• A和C相连
• B和C相连

        实际边数Ei为3，可能的边数ki * (ki - 1) / 2 = 3 * 2 / 2 = 3。

        节点i的聚类系数Ci = 2 * 3 / (3 * 2) = 1，表示节点i的邻居节点之间形成连接的概率为100%。

（三）网络属性

1.全局聚类系数

        全局聚类系数（Global Clustering Coefficient）是用来衡量整个网络中节点之间形成连接的紧密程度的指标。与局部聚类系数（节点的聚类系数）不同，全局聚类系数是对整个网络的结构进行评估，而不是针对单个节点。

        全局聚类系数的计算方法通常有两种：传统的全局聚类系数和平均全局聚类系数。

1. 传统的全局聚类系数：传统的全局聚类系数是通过计算整个网络中所有节点的局部聚类系数的平均值得出的。具体计算方法是，对于每个节点，计算其局部聚类系数，然后将所有节点的局部聚类系数求平均值，即为传统的全局聚类系数。

2. 平均全局聚类系数：平均全局聚类系数是通过计算整个网络中所有三角形的数量与所有可能形成三角形的数量之比得出的。具体计算方法是，对于网络中的每个节点，计算其邻居节点之间形成的三角形数量，然后将所有节点的三角形数量之和除以所有可能形成三角形的数量的两倍，即为平均全局聚类系数。

        全局聚类系数可以帮助我们了解整个网络的社区结构和节点之间的联系程度。一个高的全局聚类系数意味着网络中节点之间的连接更加紧密，可能存在更多的社区结构；而一个低的全局聚类系数则表示网络中节点之间的联系相对分散。通过计算全局聚类系数，我们可以更好地理解网络的整体结构和节点之间的关系。

2.网络密度

        网络密度是指一个网络中各节点之间联络的紧密程度。网络密度的取值范围是0到1之间。当网络密度接近1时，表示网络中的节点之间连接非常紧密，几乎所有节点都相互连接；而当网络密度接近0时，表示网络中的节点之间连接非常稀疏，只有少数节点之间有连接。

        一个具有个N节点和L条实际连边的网络，其网络密度为

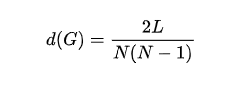
3.度分布

        度分布是图论和网络理论中的概念。一个图（或网络）由一些顶点（节点）和连接它们的边（连结）构成。每个顶点（节点）连出的所有边（连结）的数量就是这个顶点（节点）的度。度分布是对一个图（网络）中顶点（节点）度数的总体描述。对于随机图，度分布指的是图中顶点度数的概率分布。

4.平均最短路径长度

        平均最短路径是指在一个网络或图中，从一个节点到所有其他节点的最短路径的平均长度。在无向图中，最短路径是指两个节点之间通过最少的边连接的路径。

        网络中平均最短路径可以反映网络的连通性和传输效率。它衡量了网络中任意两个节点之间的平均最短距离，即需要经过多少个节点才能从一个节点到达另一个节点。一个较小的平均最短路径长度表示网络的节点之间连接紧密，信息传输速度较快，网络具有较好的传输效率。而一个较大的平均最短路径长度可能意味着网络中存在较多的障碍或瓶颈，信息传输速度较慢，网络的传输效率较低。因此，网络中平均最短路径可以反映网络的连接情况和传输效率，帮助评估网络的性能和优化网络拓扑结构。

参考文献

图算法之Centrality - 简书

复杂网络_网络图平均路径长度计算-CSDN博客

【图算法】(3) 网络的基本静态几何特征（二），附networkx完整代码_networkx计算度中心性的代码-CSDN博客

---

总结

        本文讲解了网络的基本定义，同时介绍了网络的基本属性，例如边的源节点，目标节点和权重，以及节点的中心性属性，例如度中心性、中介中心性、接近中心性以及特征向量中心性，同时介绍了网络的全局属性，例如网络密度、度分布、平均最短路径和全局聚类系数。