一元线性回归：残差值方差的无偏估计证明

在已知的前提下，证明残差的方差估计值 是 𝜎2 的无偏估计。

要证明残差的方差估计的无偏估计结果，即需要我们证明以下等式成立：

在证明这个结果成立之前，我们需要知道一些基本的知识。

我们已经知道一元线性回归的理想模型为

注意，这里指的是回归方程的模型，只有在理想情况下才能实现，所以并非是回归方程的函数形式，其函数形式的表达式为

这里我们再区分一下残差值和误差项之间的区别，对于残差值 𝑒𝑖 ，其等式的表达式为 𝑒𝑖=𝑦𝑖−𝑦𝑖^

对于误差项//，其实是一个相对抽象的概念，因为误差项定义的是理想模型中无法完全解释或捕捉的数据中的随机波动或未包含因素。再者，误差项应该服从最基本的假定，满足正态分布，即 𝜖𝑖∼𝑁(0,𝜎2) 。

具备了以上的知识基础，我们继续进行证明分析：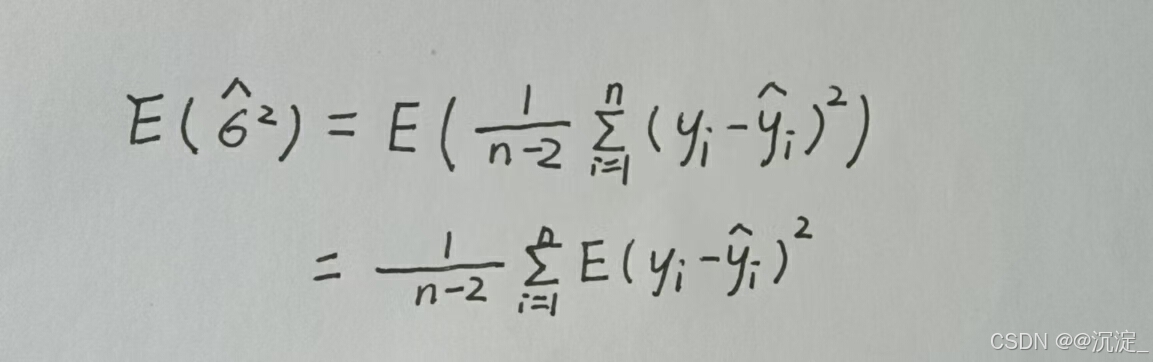

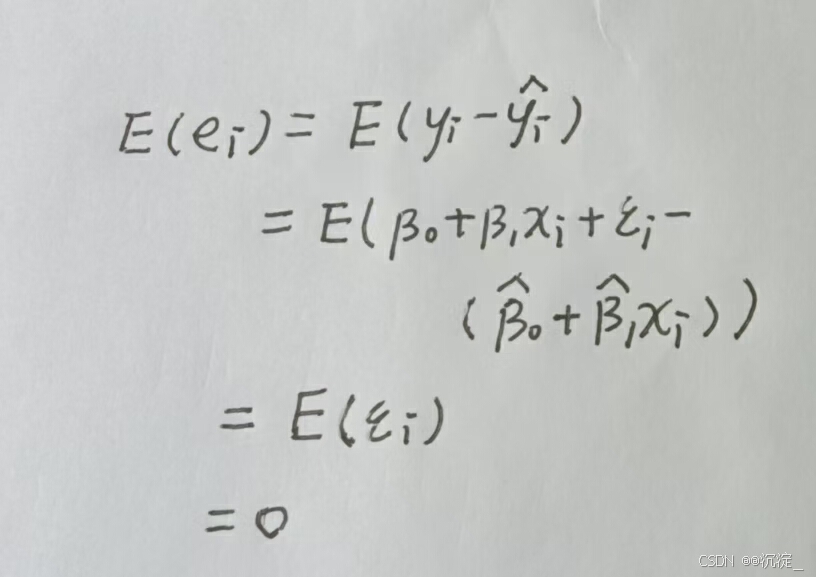
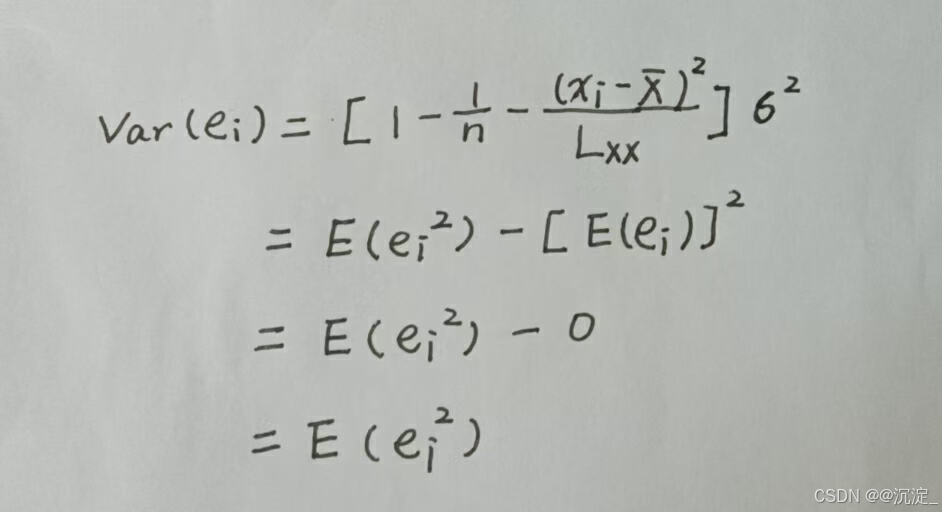
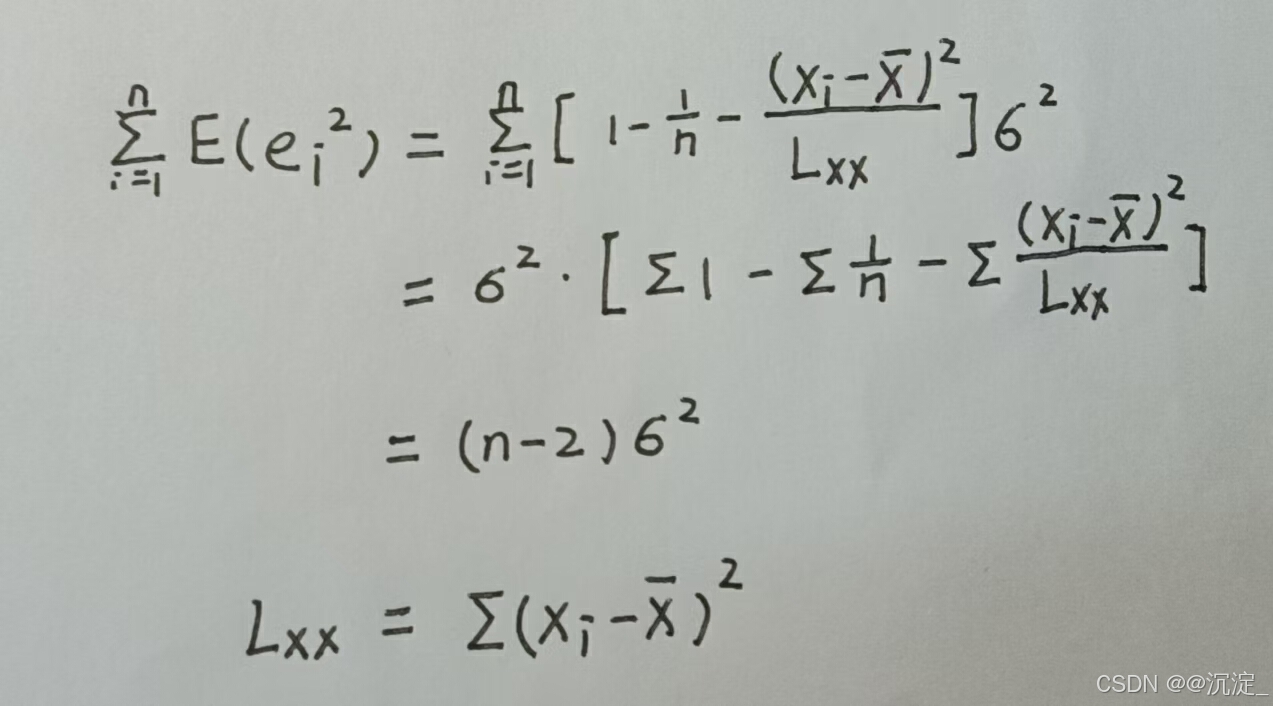
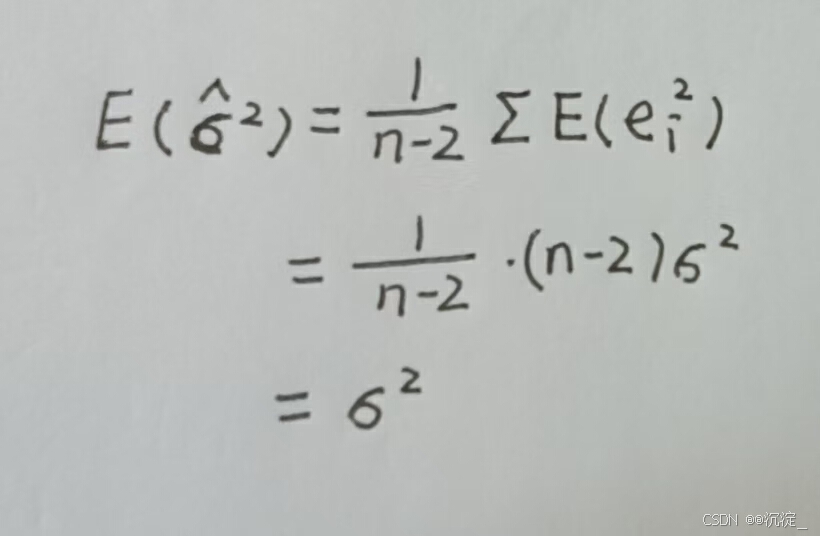
这样，即证残差的方差估计值是 𝜎2 的无偏估计。