机器学习——主成分分析

主成分分析

主成分分析概括

主成分分析（Principal Component Analysis, PCA）是一种常用的机器学习和统计学方法，用于降低数据集的维度，同时保留数据集中的重要信息。它通过线性变换将数据映射到一个新的坐标系中，使得数据在新坐标系中的每个维度（称为主成分）彼此正交且按照方差递减的顺序排列。

应用场景

降维：在高维数据中减少特征的数量，同时保留数据的关键信息，有助于可视化和模型的效率提升。

去除噪声：由于PCA将数据投影到主成分上，可以通过忽略较小的主成分来减少数据中的噪声影响。

数据压缩：将数据压缩到较低维度，有助于在存储和计算方面节省成本。

降维要求

1）最大可分性：降维之后的数据点之间的距离最远。
2）最近重构性：降维之前的点距离投影线或投影面距离最近。

举例：如图，将样本投影到M上明显比投影到N上点与点之间的距离更远，并且投影点距离M的长度明显比N点的近，所以满足了最大可分性和最近重构性。

PCA的步骤

数据中心化

首先，对原始数据进行中心化处理，即将每个特征的均值减去所有样本对应特征的均值，使得数据的均值为零。
目的：消除数据中的平均值，使得数据的均值为零。这个过程通常在数据预处理阶段进行，在应用某些机器学习算法或统计分析之前进行。

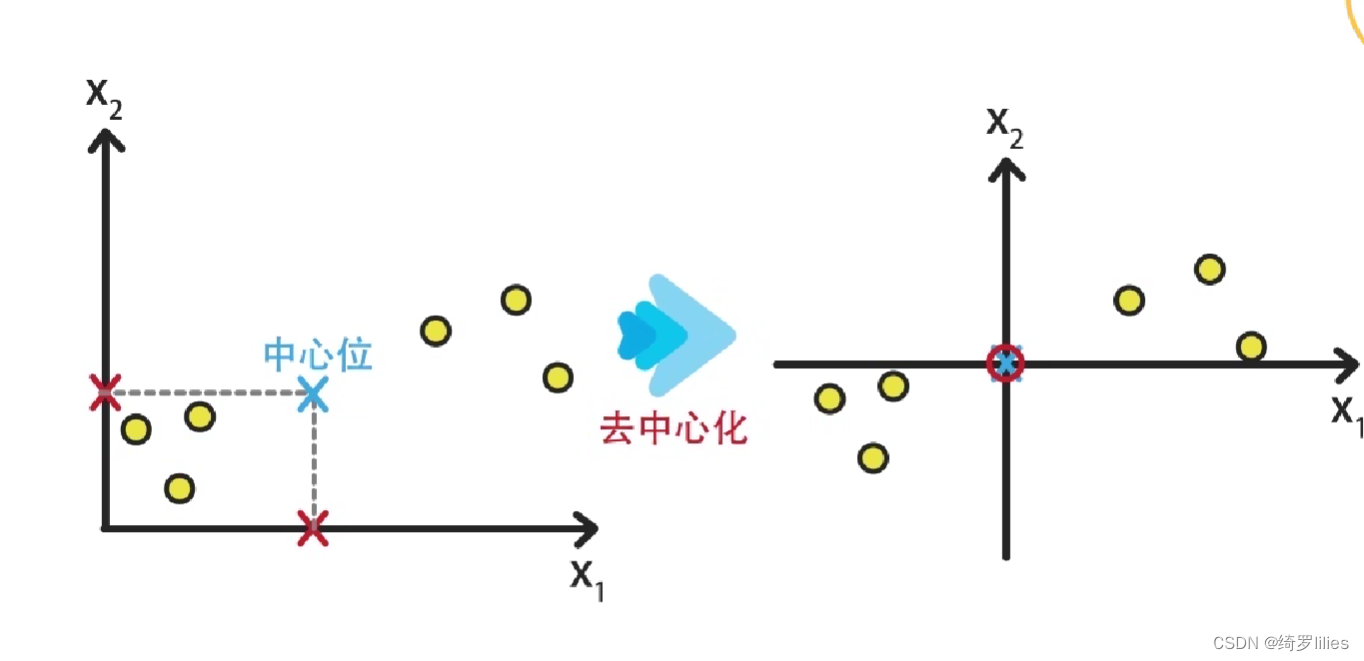
举例：在如图所示的六个点中，分别计算特征值X1和X2的均值，并且在图中标出即为蓝色叉子的点，之后将X轴和Y轴分别向蓝色点平移，将远点置于蓝色点的位置即为去中心化。去中心化并不会影响特征之间的关系，但是可以让之后的运算实现算法更加的方便。

计算协方差矩阵：

（1）协方差：在统计学中，协方差描述了两个随机变量之间的关系。如果两个变量的协方差为正值，表示它们具有正相关性；如果为负值，则表示它们之间存在负相关性。在主成分分析中，通过计算原始数据的协方差矩阵来确定数据之间的相关性，从而找到数据中的主成分。

（2）方差：方差表示一个随机变量与其均值之间的差异程度，是协方差的一种特殊形式，即两个变量相同时的协方差即为它们自身的方差。在主成分分析中，方差也被用来衡量数据中的变异性，方差越大，表示数据的变化范围越广。

（3）协方差矩阵：协方差矩阵是一个对称矩阵，其中对角线上的元素是各个变量的方差，非对角线上的元素是相应变量之间的协方差。在主成分分析中，协方差矩阵是一个重要的概念，通过对协方差矩阵进行特征分解，我们可以找到数据中的主成分方向，并且可以通过主成分的重要性（即方差）来选择最重要的主成分。

特征值分解

对协方差矩阵进行特征值分解（或奇异值分解），得到特征值和对应的特征向量。特征向量表示新坐标系的方向，特征值表示在该方向上的方差大小.对于一个给定的方阵A，它的特征向量（eigenvector，也译固有向量、本征向量）经过这个线性变换之后，得到的新向量仍然与原来的保持在同一条直线上，但其长度或方向也许会改变。即以下关系式：Av=λv.其中λ（特征值）为标量，即特征向量的长度在该线性变换下缩放的比例。如果特征值为正，则表示v在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回原点。

举个例子：

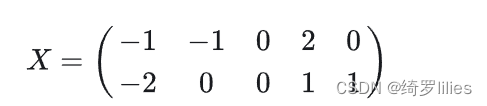
以X为例，我们用PCA方法将这两行数据降到一行。

1)因为X矩阵的每行已经是零均值，所以不需要去平均值。

2)求协方差矩阵：

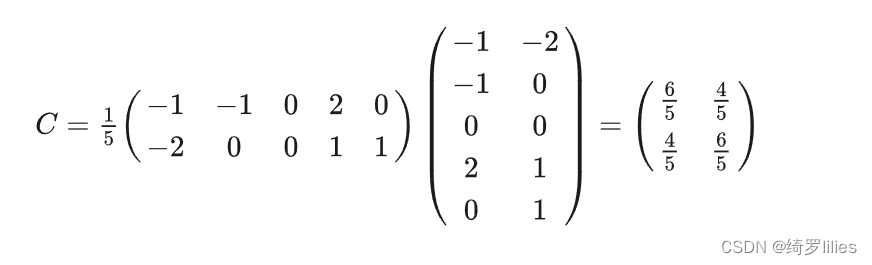
3)求协方差矩阵的特征值与特征向量。

求解后的特征值为：λ1 = 2，λ2 = 2/5，对应的特征向量为：

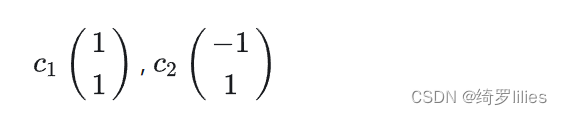
其中对应的特征向量分别是一个通解，c1和c2可以取任意实数。那么标准化后的特征向量为：

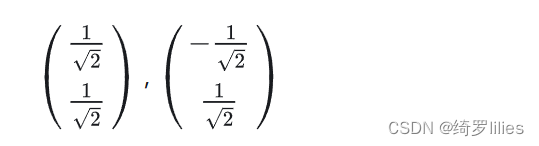
4)矩阵P为：

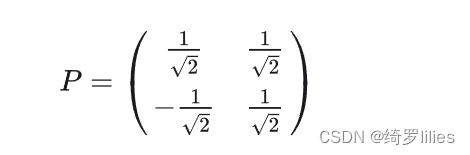
5)最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：

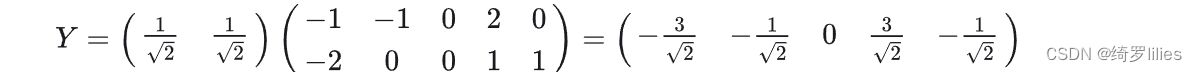
代码实现

import matplotlib.pyplot as plt
import sklearn.decomposition as dp
from sklearn.datasets import load_iris
 
x,y=load_iris(return_X_y=True) #加载数据，x表示数据集中的属性数据，y表示数据标签
pca=dp.PCA(n_components=2) #加载pca算法，设置降维后主成分数目为2
reduced_x=pca.fit_transform(x) #对原始数据进行降维，保存在reduced_x中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)): #按鸢尾花的类别将降维后的数据点保存在不同的表中
    if y[i]==0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
    elif y[i]==1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

结果：

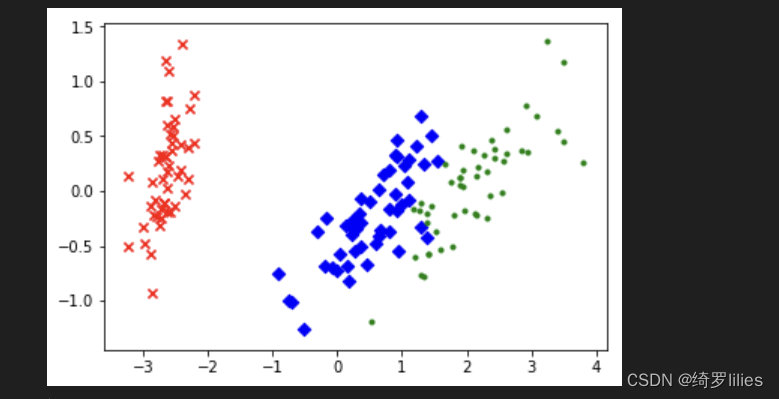
实验小结

PCA是一种使用最广泛的数据降维算法，主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。特征约减的目的是将高维特征向量映射到低维子空间中；无监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩去噪，因此应用很广泛。

优点：简单易实现；仅需要以方差衡量信息量，不受数据集以外的因素影响；各主成分之间正交，可消除原始数据成分间的相互影响的因素。

缺点：主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。