用Python排班休息

1.场景：

公司有A、B、C三位客服，需要每周安排三人轮流周五、周六、周日休息一天，已知3月有5个周末，每人尽量安排在周六日（客服更想周末休），尽量每人的休息间隔不要太久（太劳累）

2.要求：

1. 员工人数3人：A、B、C
2. 每周轮流休息一天：周五、周六、周日
3. 3月有5个周末
4. 每人尽量安排休息周六日
5. 每人尽量休息间隔太久

3.方案：

因3月有5个周末，所以一共休息日是5个周五、5个周六、5个周日。为公平起见，每人都尽量多安排周六日，少安排周五。因此，A、B、C通过抓阄选出自己的休息方案如下。
        

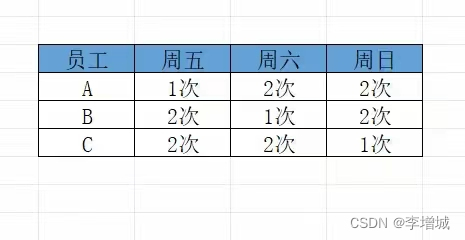
• A：1次周五、2次周六、2次周日
• B：2次周五、1次周六、2次周日
• C：2次周五、2次周六、2次周日

4.休息排序

每个人的休息日的排序组合：
5：周五、6：周六、7：周日

• 每个人有30种休息日组合方式
• 用程序分别组合A、B、C的休息组合，A的30种 X  B的30种  X  C的30种  = 27000种组合
• 27000种组合中，只有一部分是正确的（例如A休息周五时，其他人不能冲突）

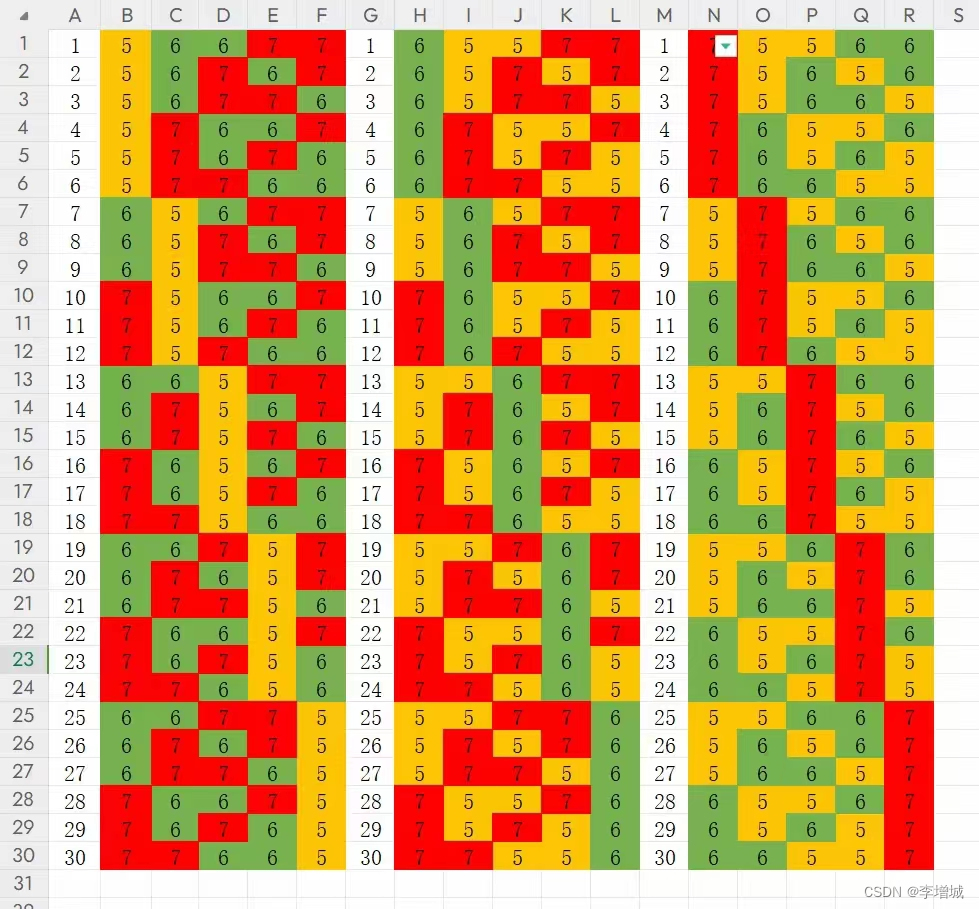
5.代码

        

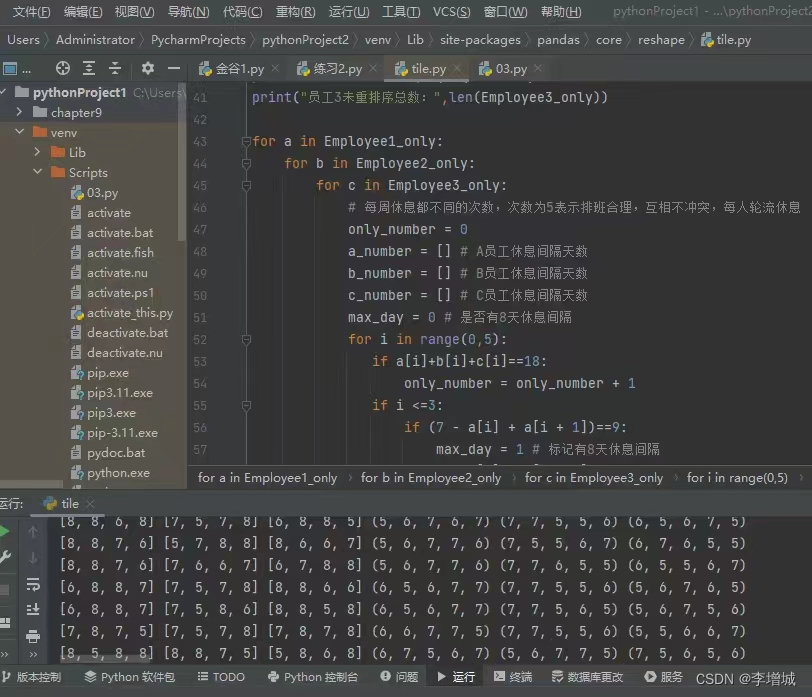
import itertools

# 用数字1-7代表周一到周日
a=[5,6,6,7,7]
result=itertools.permutations(a,5)
print(type(result))
Employee1=list(result)
print("员工A未去重排序：",Employee1)
print("员工A未去重排序总数：",len(Employee1))
Employee1_only = []
for i in Employee1:
    if i not in Employee1_only:
        Employee1_only.append(i)
print("员工A去重排序：",Employee1_only)
print("员工A未重排序总数：",len(Employee1_only))

解释：itertools库提供了多个函数，用于生成不同类型的组合迭代器，例如排列、组合、笛卡尔积等。这些函数包括 permutations、combinations、product 等。

以上代码实现员工A的休息日的排序组合

b=[5,5,6,7,7]
result=itertools.permutations(b,5)
print(type(result))
Employee2=list(result)
print("员工B未去重排序：",Employee2)
print("员工B未去重排序总数：",len(Employee2))
Employee2_only = []
for i in Employee2:
    if i not in Employee2_only:
        Employee2_only.append(i)
print("员工B去重排序：",Employee2_only)
print("员工B未重排序总数：",len(Employee2_only))

以上代码实现员工B的休息日的排序组合

c=[5,5,6,6,7]
result=itertools.permutations(c,5)
print(type(result))
Employee3=list(result)
print("员工C未去重排序：",Employee3)
print("员工C未去重排序总数：",len(Employee3))
Employee3_only = []
for i in Employee3:
    if i not in Employee3_only:
        Employee3_only.append(i)
print("员工C去重排序：",Employee3_only)
print("员工C未重排序总数：",len(Employee3_only))

以上代码实现员工C的休息日的排序组合

for a in Employee1_only:
    for b in Employee2_only:
        for c in Employee3_only:
            # 每周休息都不同的次数，次数为5表示排班合理，互相不冲突，每人轮流休息
            only_number = 0
            a_number = [] # A员工休息间隔天数
            b_number = [] # B员工休息间隔天数
            c_number = [] # C员工休息间隔天数
            max_day = 0 # 是否有8天休息间隔
            for i in range(0,5):
               if a[i]+b[i]+c[i]==18:  # 单周中A、B、C不冲突，周五（5）周六（6）周日（7）
                   only_number = only_number + 1
               if i <=3:
                   if (7 - a[i] + a[i + 1])==9:
                       max_day = 1 # 标记有8天休息间隔
                   if (7 - b[i] + b[i + 1])==9:
                       max_day = 1 # 标记有8天休息间隔
                   if (7 - c[i] + c[i + 1])==9:
                       max_day = 1 # 标记有8天休息间隔
                   a_number.append(7 - a[i] + a[i + 1])
                   b_number.append(7 - b[i] + b[i + 1])
                   c_number.append(7 - c[i] + c[i + 1])
            if (only_number == 5)&(max_day == 0):
                print(a_number,b_number,c_number,a,b,c)

解释：分别3次for循环获取A、B、C的组合之一，有27000种组合

• max_day：若A、B、C中的休息间隔有8天以上，排除不要
• only_number：单周中A、B、C休息不冲突，则only_number值加1，                          
• 若only_number最终值为5，表示5周都不冲突，排班正确，否则排班错误排除
• a_number：A的所有休息日之间的间隔天数
• b_number：B的所有休息日之间的间隔天数
• c_number：C的所有休息日之间的间隔天数

6.筛序最佳方案：

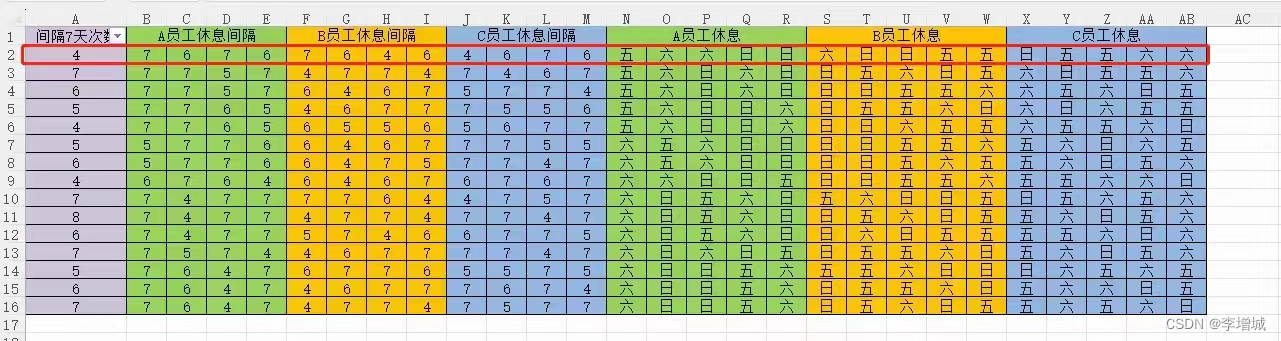
A 列计算每个组合A、B、C中间休7天共有多少个

尽量选择间休7天总数量少的，每个人间休7天次数也不能太多且尽量错开（不要连续间休7天）

从上表中看，间休7天总数6人次和7人次首先排除，整体员工工作时间长，过于劳累

最终选红框（第二行）：

•         1.间休7天总数最少，只有4人次
•         2.间休日差异小，人均6天左右
•         3.员工A只有一次周五，比别人少一次，所以A员工间休7天有2次，比其他人多一次，分              配更公平。