【木桶效应】

题目：

给定一个长度为n的整数数组height。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i])。 找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明：你不能倾斜容器。
示例 1：
输入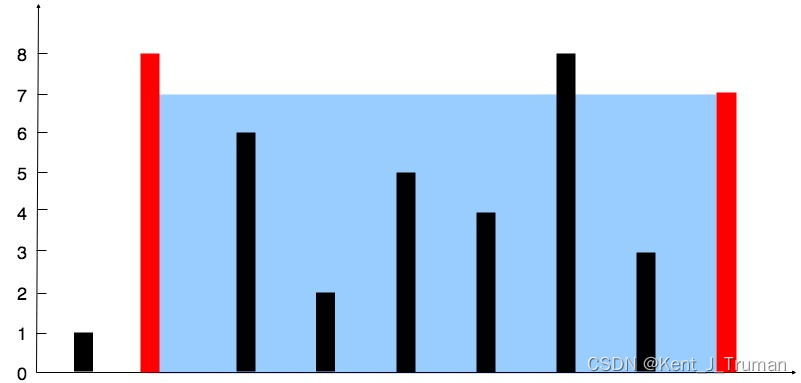：[输入：[1,8,6,2,5,4,8,3,7]输出：49解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
示例 2：输入：height = [1,1]输出：1。

思路：

1. 二重循环？O(n方)
2. 某种贪心策略？O(n)

1.代码：

#include<bits/stdc++.h>

using namespace std;

int axis[10010];

int main()
{
    int i = 0;
    char c;
    do{ cin >> axis[++i]; }
    while(c = getchar(), c != '\n');

    int biggest_area = 0;
    for(int m = 1; m <= i; m++)
    {
        for(int n = m+1; n <= i; n++)
        {
            int area;

            area = (n-m) * (axis[n] > axis[m] ? axis[m] : axis[n]);
            if(area > biggest_area) biggest_area = area;
        }
    }

    cout << biggest_area << endl;

    return 0;
}

2.代码：

public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                max(res, (j - i) * height[i++]): 
                max(res, (j - i) * height[j--]); 
        }
        return res;
    }

谈一谈对这个贪心策略的理解：

采用方法是双指针法。

策略是每次收缩高度较小的那个指针，如果高度相同则收缩j。

为什么会有效呢？

我认为首先初态是宽度最大的情况，如果收缩较大的指针，水的有效高度不会变大，反而宽度一定会变小；如果收缩较小的指针，有可能会使得新的有效高度变大（当然也可能不变，变小），从而有可能使得水更多（当然也可能宽度减小的影响更大，导致不变，变小）。于是，通过逐步选择可能带来更优情况的原子性的收缩操作（原子性的操作每个状态只有两种），该算法可以遍历每一个潜在更优的res，包含住可能存在于内层的指针状态。

最后总结一下：这个最优状态一定是通过若干个原子性操作得到的，而且不可能由某个状态通过一次绝对无法更优的选择得到，而必然是由某个状态通过一次可能更优的选择得到。