感知机及其python实现

分类模型；找到一个超平面$\vec{w}\vec{x}+b=0$ 大于0进行分类判断；感知机也可以看成一个单层神经网络

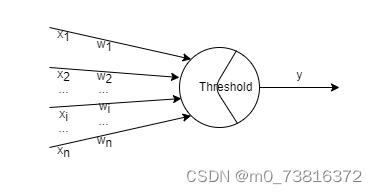
1. 模型

$$\begin{gathered} z=\vec{w}\cdot \vec{x}+b=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b \\ y=sign(z)=\{\begin{array}{l}1,z\ge 0\\ -1,z<0\end{array} \end{gathered}$$

2. 损失函数

$$J(w)=-\sum _{x_i\in M}{y}^{(i)}(\vec{w}\cdot {\vec{x}}^{(i)}+b)$$

其中M为错误分类的样本点集合，$\vec{w},{\vec{x}}^{(i)}$ 都是n维的向量，点表示内积运算

3. 损失函数的原理推导

损失函数的几何意义为所有错误分类样本点距离超平面$\vec{x}\vec{w}+b=0$ 的距离之和，接下来证明两点

• $\vec{w}$ 为超平面的法向量

  假设O为坐标原点，P1， P2为超平面上的任意两点，其坐标分别为为${\vec{x}}^{(1)}和{\vec{x}}^{(2)}$ ， 因此$\vec{w}和\overrightarrow{P1P2}$ 的內积为：
  $$\begin{gathered} \vec{w}\cdot \overrightarrow{P_1{P}_2}=\vec{w}\cdot (\overrightarrow{O{P}_2}-\overrightarrow{O{P}_1}) \\ =\vec{w}({\vec{x}}^{(1)}-{\vec{x}}^{(2)}) \\ =-b-(-b)=0 \end{gathered}$$
  因此得证$\vec{w}$ 为超平面的法向量

• 误分类点到超平面的距离公式为 $d=-y^{(i)}(\vec{w}\cdot {\vec{x}}^{(i)}+b)$

  设坐标原点为O， 误分类点为P，其在超平面的投影点为P’,其坐标分别为为$\vec{x}和\vec{x}’$ 因为$\overrightarrow{P^{\prime }P}$ 和$\vec{w}$ 平行，所以其內积的绝对值为两向量的模的乘积
  $$|\vec{w}\cdot \overrightarrow{P^{\prime }P}|=||\vec{w}|{|}_2\ast d$$
  又因为P’在超平面上， 因此有$\vec{w}\cdot {\vec{x}}^{\prime }+b=0$
  $$\begin{gathered} |\vec{w}\cdot \overrightarrow{P^{\prime }P}|=|\vec{w}\cdot (\overrightarrow{OP}-\overrightarrow{O{P}^{\prime }})| \\ =|\vec{w}\cdot (\vec{x}-{\vec{x}}^{\prime })| \\ =|\vec{w}\cdot \vec{x}+b| \end{gathered}$$
  最后，因为对于误分类点必定满足$y^{(i)}(\vec{w}\cdot {\vec{x}}^{(i)}+b)<0$ ， 因此得误分类点到超平面的距离公式为 $d=-y^{(i)}(\vec{w}\cdot {\vec{x}}^{(i)}+b)$

4. python实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

def model(X, theta):
    return X @ theta

def predict(x, theta):
    flags = model(x, theta)
    y = np.ones_like(flags)
    y[np.where(flags < 0)[0]] = -1
    return y

def computerCost(X, y, theta):
    y_pred = predict(X, theta)
    error_index = np.where(y_pred != y)[0]
    return np.squeeze(-y_pred[error_index].T @ y[error_index])


def gradientDescent(X, y, alpha, num_iters=1000):
    # m = X.shape[0]
    #X = np.hstack((np.ones((m, 1)), X))
    #y = y[:, np.newaxis]
    n = X.shape[1]
    theta = np.zeros((n, 1))
    J_history = []
    for i in range(num_iters):
        y_pred = predict(X, theta)
        error_index = np.where(y_pred != y)[0]
        theta = theta + alpha * X[error_index, :].T @ y[error_index]
        cur_cost = computerCost(X, y, theta)
        J_history.append(cur_cost)
        print('.', end='')
        if cur_cost == 0:
            print(f'Finished in advance in iteration {i+1}!')
            break
        
    return theta, J_history

一个实例

iris = datasets.load_iris()
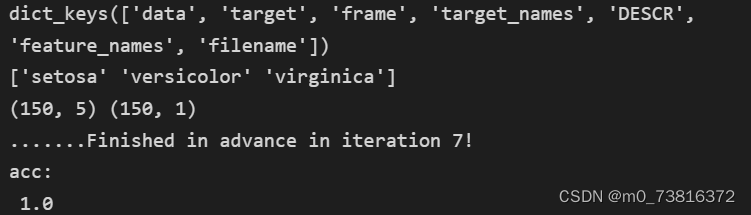
print(iris.keys())
print(iris.target_names)
X = iris.data
m = X.shape[0]
X = np.hstack((np.ones((m, 1)), X))
y = iris.target
y[np.where(y!=0)[0]] = -1
y[np.where(y==0)[0]] = 1
y = y.reshape((len(y), 1))
print(X.shape, y.shape)
theta, J_history = gradientDescent(X, y, 0.01, 1000)
y_pred = predict(X, theta)

acc = np.sum(y_pred == y)/len(y)
print('acc:\n', acc)

结果