C浮点型的比较方法

---

前言

本文说明浮点型为什么会有精度丢失，并且如果精度丢失需要用什么样的方法去比较两个浮点型

---

一、精度丢失

  为什么浮点型会存在精度丢失，这主要取决于浮点型在内存中的存储方式,精度丢失一般发生在小数，这是因为在表示某些特定的数值时，小数二进制无法完整的表达

$$(-1{)}^S\ast M\ast 2^E$$

根据以上公式，因为9.6为正数，所以S=0,M的整数部分为9，转换成二进制为1001，小数部分为0.6是表示不了的，这是为什么呢？如图

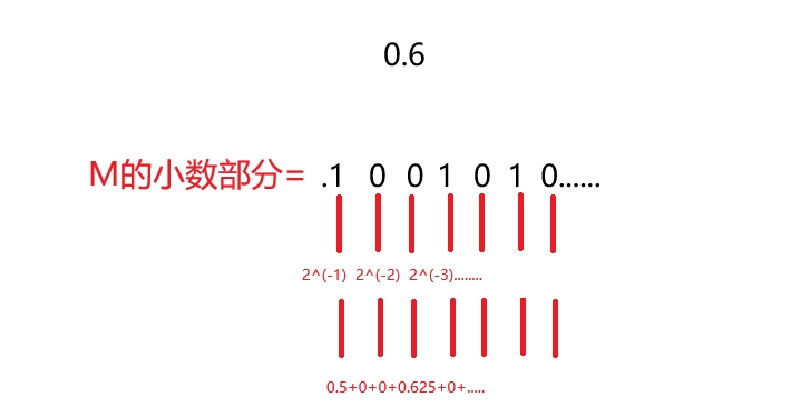
可以看到小数部分不管怎么样凑都凑不到0.6，double类型只有八个字节，把八个字节都使用完也凑不到0.6的时候，就会发生精度损失，这就是浮点型精度损失的原理

---

二、比较方法

2.1常规比较方法

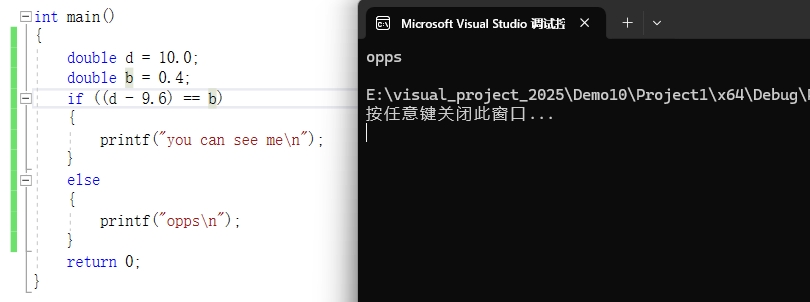
我们在使用两个数据比较的时候通常使用 " == " 来比较，由上面标题可知，浮点数是有精度丢失的，严格来说是不能使用 " == " 来比较的

2.2范围比较方法

2.2.1 精度宏介绍

在介绍比较方法前，先介绍C库自带的两个宏

• DBL_EPSILON：double类型的精度损失范围
• FLT_EPSILON：float类型的精度损失范围

由于浮点数是有精度损失的，那么我们是不是就可以理解为，我们比较的时候，两个值的大小差值在精度损失的范围内，就可以理解为这两个数是相等的，当然这个精度也可以我们自己定义，只不过自己定义不太准确，因此C库就提供了这两个宏给我们做浮点型比较的时候使用,有一点要注意，这两个宏只适用于1左右的数字的比较，因为范围太小，如果想比较两个较大的数字要自己定义更加合适的精度

2.2.2比较方法

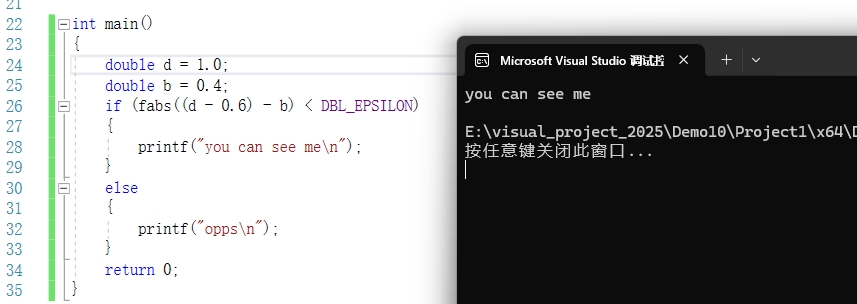
知道了原理我们可以使用以下的比较方式来比较两个浮点型是否相等，当然两个浮点数有大有小，所以计算出的结果需要使用fabs函数来求绝对值
$$fabs(x-y)<DBL\_EPSILON$$

#include <stdio.h>

#include <float.h> //精度宏的头文件
#include <math.h> //fabs函数的头文件

int main()
{
	double d = 1;
	double b = 0.4;
	if (fabs((d - 0.6)- b) < DBL_EPSILON)
	{
		printf("you can see me\n");
	}
	else
	{
		printf("opps\n");
	}
	return 0;
}

---

三、总结

浮点数精度损失是因为在内存中的存储方式导致的，无法改变，比较两个浮点数只能取对应的精度范围来比较，C标准库提供的两个精度宏只适用于数字1左右的比较，如果想比较更大的数字需要自己定义合适的精度范围