质因数的相关算法

积性函数

• 积性函数基本都可用线性筛（欧拉筛）求解。
  $$\begin{gathered} ①定义在所有正整数上的函数称为算术函数(或者数论函数) \\ ②如果算术函数f对任意两个互素的正整数p和q，均有f(pq)=f(p)f(q)，称为积性函数（乘性函数） \\ ③如果对任意两个正整数p和q均有f(pq)=f(p)f(q)，则为完全积性函数 \\ ④积性函数的和函数，也是积性函数。若f是积性函数，则F(n)={\Sigma }_{d|n}f(d)也为积性函数。d|n表示d是n的因子。 \end{gathered}$$
  • 常见算法问题：
    (1)算f的第n项$f(n)$
    (2)算f在1到n的所有项：$f(1),f(2),...,f(n)$
    (3)算f前n项的和${\Sigma }_{i=1}^{n}f(i)$，即前缀和

---

质因数

• 试除法求判定质数：

  • 即通过暴力算法求质数

  • 题目来源：Acwing 866：试除法判定质数

  • 时间复杂度$O(\sqrt{n})$

  • 优化原理（见代码注释处）：对于一个数x，若是合数，则必可以拆分为2个约数（一大一小），若在i <= sqrt(x) <--> i*i <= x范围内，找不到小约数，则表示该数x是质数。

  #include<iostream>
  #include<cmath>
  using namespace std;
  
  int a[110];
  
  int main()
  {
      ios::sync_with_stdio(0);
      cin.tie(0),cout.tie(0);
      int n;
      cin>>n;
      for(int i = 0; i < n; i++)
      {
          cin>>a[i];
          int flag = 1;
          if(a[i] < 2)
          {
              cout<<"No"<<endl; //1不是素数
              continue;
          }
          for(int j = 2; j<= a[i]/j; j++) //优化处，优化前为：j<=a[i]
          {
              if(a[i] % j == 0) 
              {
                  flag = 0;
                  cout<<"No"<<endl;
                  break;
              }
          }
          if(flag)
              cout<<"Yes"<<endl;
      }   
  }
  

• 试除法分解质因数

  • 将一个合数分解成质因数相乘的形式：$n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}...p_k^{{\alpha }_k}$
  • 分解质因数时，分解出的最后一个质因数可能大于$\sqrt{n}$，例如：10以内的质因数：$2和5，\sqrt{10}<5$ 所以5是未被循环代码算入，需特判。
  • 题目来源：Acwing 867：试除法判定质数

  #include<iostream>
  #include<cmath>
  using namespace std;
  
  int a[110];
  
  int main()
  {
      ios::sync_with_stdio(0);
      cin.tie(0),cout.tie(0);
  
      int n;
      cin>>n;
  
      for(int i = 0; i < n; i++)
      {
          cin>>a[i];
          int num = a[i];
          for(int j = 2; j <= sqrt(a[i]); j++) //不可能超过一半的数相乘的。有也就顶多只有1位
          {
              if(num % j == 0) //no a[i], is num, 会变的。
              {
                  int s = 0;
                  while(num % j == 0) num /= j, s++;
                  cout<<j <<" "<<s<<endl;
              }
          }
          if(num > 1) cout<<num <<" "<<1<<endl;//特判大于sqrt(a[i])的质因数
          cout<<endl;
      }
      return 0;
  }
  

• 朴素筛法（埃氏筛法）求素数

  • $时间复杂度：O(NloglogN)$
  • 题目来源：Acwing 868：筛质数

  #include <iostream>
  #include <algorithm>
  #include <cstring>
  #include <cmath>
  using namespace std;
  
  const int N = 1e6+10;
  int prime[N];//记录质数
  bool vis[N]; //筛去合数
  //埃氏筛
  void E_sieve(int n)
  {
      int num = 0; //记录素数个数
      memset(vis, false, sizeof vis);
      for(int i = 2; i <= sqrt(n); i++) //合数k一定可以被小于都等于sqrt(k)内的一个素数整除，eg:25:5*5，3*8=24,约数定理。约数成对出现
      {
          //素数都是false，未被true掉
          if(vis[i]) continue; //合数
          for(int j = i*i; j <= n; j += i) //+=i,因为每次都是倍数。而不是+1+1+1.。。
              vis[j] = true; //i*i，优化，因为前面的合数已被小的素数筛掉。
      }
      for(int i = 2; i <= n; i++)  //从2开始。小于=n，n也可能是素数。1不是素数，所以从2开始。
          if(!vis[i])
              prime[num++] = vis[i];
      cout<<num;
  }
  int main()
  {
      int n;
      cin>>n;
      E_sieve(n);
  }
  

• 欧拉筛法（线性筛)

  • 时间复杂度：$O(n)$
  • 欧拉筛法确保每个合数只被筛一遍，即只被其最小质因数筛掉。核心代码：if(i % prime[j] == 0) break;
  • 如图：
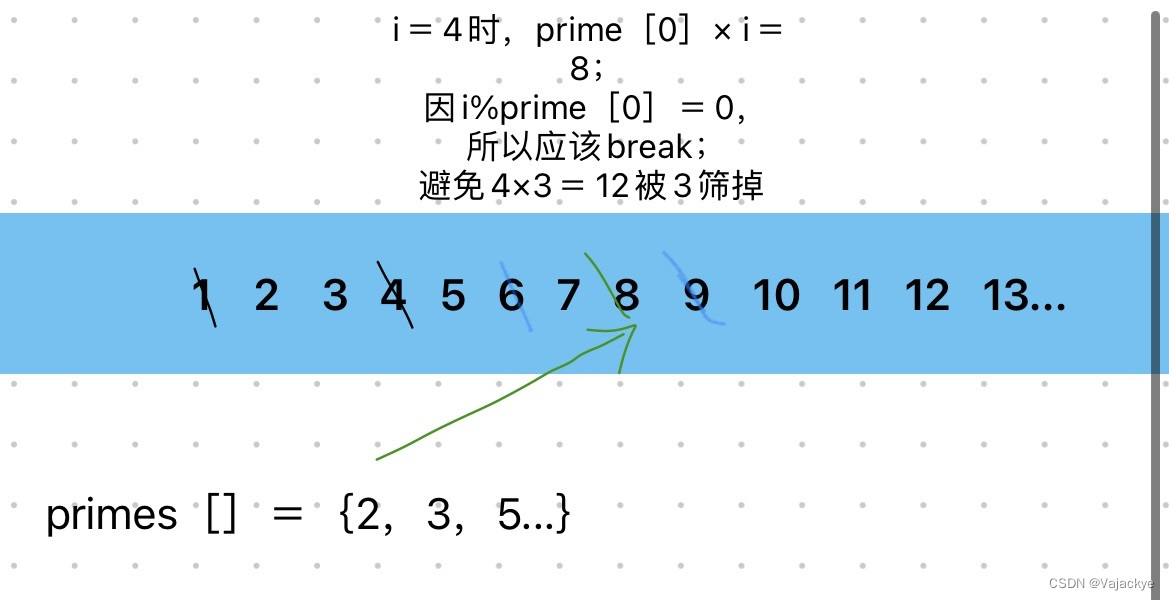
  • 详细内容见：Vajackye的github–数论

  #include <iostream>
  #include <algorithm>
  #include <cstring>
  #include <cmath>
  using namespace std;
  
  const int N = 1e6+10;
  int prime[N];//记录质数
  bool vis[N]; //筛去合数
  
  //欧拉筛,线性筛
  void Euler_sieve(int n)
  {
      int num = 0; //记录素数个数
      memset(vis, false, sizeof vis);
      memset(prime, 0, sizeof prime);
      for(int i = 2; i <= n; i++) //从2开始筛出所有素数
      {
          //素数，开头为2
          if(!vis[i]) prime[num++] = i;
          //筛prime素数组内的所有素数，筛最近的，避免重复筛，2->8,3->×(12，应该被2筛，被最小质数筛出)
          for(int j = 0; j < num; j++)//依次利用每个素数
          {
              if(i * prime[j] > n) break; //筛出在n范围内的素数（超出题目范围略）
              vis[prime[j] * i] = true; //按照i的倍数，依次筛出后面的素数。
              if(i % prime[j] == 0) break; //i是该素数的合数，则退出，因为，下一个素数*i 一定是本素数的合数，不满足：最小被素数除
          }
      }
      cout<<num;
  }
  
  int main()
  {
      int n;
      cin>>n;
      //E_sieve(n);
      Euler_sieve(n);
  }