介绍
决策树是一种直观的决策支持工具,广泛应用于机器学习和数据分析中。它通过树状结构来表示决策过程中的各种可能性及其可能的后果。决策树的每个内部节点代表一个属性(特征)的测试,每个分支代表一个测试结果,而每个叶节点代表最终的决策或结果。
类别
ID3算法——信息增益
ID3算法(Iterative Dichotomiser 3)是一种利用信息增益作为标准来构建决策树的算法。信息增益是通过比较特征分割前后的熵来计算的。熵值越低代表信息越纯,效果越好。熵计算公式如下:
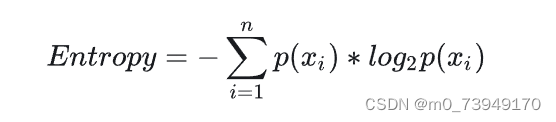
其中,𝑝𝑖pi是数据集中第i个类别的概率。
则可以计算出信息增益,公式如下
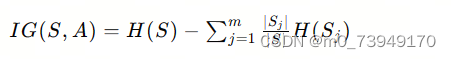
其中,S是数据集,A是特征,m是特征A的可能值的数量,Sj是数据集S在特征A的条件下,取第j个值的子集。
C4.5算法——信息增益比
C4.5算法是ID3算法的改进。C4.5使用信息增益比(Gain Ratio)而不是ID3算法中的信息增益来选择属性,这有助于减少过拟合的风险,并处理具有多个类别的属性。可以处理连续属性,它通过选择一个分割点将属性值分为两部分来处理连续属性。
信息增益比是信息增益除以属性的固有值:
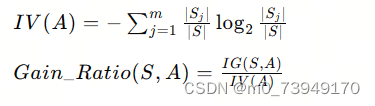
其中,S是数据集,A是特征,m是特征A的可能值的数量,Sj是数据集S在特征A的条件下,取第j个值的子集。
CART算法——基尼指数
CART生成的是二叉树,每个内部节点都有两个分支,这与ID3和C4.5算法不同,后两者可以生成多叉树。CART使用纯度损失(如基尼不纯度或交叉熵)来评估分裂的好坏。
基尼不纯度公式如下:
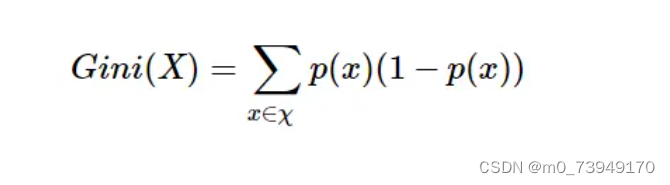
其中,X是数据集,px是数据集中第x个类别出现的概率。
算法介绍
本博客介绍ID3算法和CART算法
数据集
def createDataSet():
labels = ['Outlook', 'Temperature', 'Humidity', 'Wind', 'Play']
dataSet = [
['sunny', 'hot', 'high', 'false', 'no'],
['sunny', 'hot', 'high', 'true', 'no'],
['overcast', 'hot', 'high', 'false', 'yes'],
['rainy', 'mild', 'high', 'false', 'yes'],
['rainy', 'cool', 'normal', 'false', 'yes'],
['rainy', 'cool', 'normal', 'true', 'no'],
['overcast', 'cool', 'normal', 'true', 'yes'],
['sunny', 'mild', 'high', 'false', 'no'],
['sunny', 'cool', 'normal', 'false', 'yes'],
['rainy', 'mild', 'normal', 'false', 'yes'],
['sunny', 'mild', 'normal', 'true', 'yes'],
['overcast', 'mild', 'high', 'true', 'yes'],
['overcast', 'hot', 'normal', 'false', 'yes'],
['rainy','mild', 'high', 'true', 'no']
]
return dataSet,labelsID3代码
构造树
def createTree(dataset, labels, featlables):
classList = [example[-1] for example in dataset] #得到最后一个标签
if classList.count(classList[0]) == len(classList):
return classList[0] #标签全为一个类型时,即可结束
if len(dataset[0]) == 1:
return majoritycnt(classList) #只是最后一个数据集时,判断其中标签类型哪一个多即为哪一个
bestFeat = chooseBestFeatureToSplit(dataset) #得到最好的数据集的下标
bestFeatLabel = labels[bestFeat]
featlables.append(bestFeatLabel) #将其标签添加
myTree = {bestFeatLabel:{}} #构成树
del labels[bestFeat] #删除标签
featValue = [exampel[bestFeat] for exampel in dataset]
uniqueVals = set(featValue) #得到叶子结点
for value in uniqueVals: #用剩余数据集继续构建树
sublabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataset,bestFeat,value),sublabels,featlables)
return myTree当无法继续得到叶节点时候,有两种情况,一种为全为样本中的yes或者no则可以直接返回,另一种则既有yes也有no,则需要判断二者谁多
def majoritycnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] = classCount[vote] + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]信息增益计算
def chooseBestFeatureToSplit(dataset): #信息增益
numFeatures = len(dataset[0]) -1 #数据集除去标签后的数据特征个数
baseEntropy = calcShannonEnt(dataset) #初始熵值
bestInfoGain = 0
bestFeaturn = -1
for i in range(numFeatures):
featList = [example[i] for example in dataset]
uniqueVals = set(featList)
newEntropy = 0
for val in uniqueVals:
subDataSet = splitDataSet(dataset,i,val) #去除该列的数据集
prob = len(subDataSet)/float(len(dataset))
newEntropy += prob*calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeaturn = i
return bestFeaturn这里可以使用calcShannonEnt(dataset)计算初始熵值,也可以计算类别的熵值
def calcShannonEnt(dataset):
numExamples = len(dataset)
labelCounts = {}
for featVec in dataset:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 #计算标签的个数
shanNonEnt = 0
for key in labelCounts:
prop = float(labelCounts[key])/numExamples
shanNonEnt -= prop*math.log(prop,2)
return shanNonEntsplitDataSet(dataset,i,val)函数用于将计算完熵值的类别进行删除,即便于计算熵值,也可以用于选出最佳特征后,计算第二好特征
def splitDataSet(dataset,axis,val):
retDataSet = []
for featVec in dataset:
if featVec[axis] == val:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSetCART算法
与ID3代码区别即为calcShannonEnt(dataset)的区别,构造树的代码与分裂数据集代码一致
构造树
def createTreeGini(dataset, labels, featlables):
classList = [example[-1] for example in dataset] #得到最后一个标签
if classList.count(classList[0]) == len(classList):
return classList[0] #标签全为一个类型时,即可结束
if len(dataset[0]) == 1:
return majoritycnt(classList) #只是最后一个数据集时,判断其中标签类型哪一个多即为哪一个
bestFeat = chooseBestFeatureToSplitGini(dataset) #得到最好的数据集的下标
bestFeatLabel = labels[bestFeat]
featlables.append(bestFeatLabel) #将其标签添加
myTree = {bestFeatLabel:{}} #构成树
del labels[bestFeat] #删除标签
featValue = [exampel[bestFeat] for exampel in dataset]
uniqueVals = set(featValue) #得到叶子结点
for value in uniqueVals: #用剩余数据集继续构建树
sublabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataset,bestFeat,value),sublabels,featlables)
return myTree基尼指数计算
def getGini(dataset):
numData = len(dataset)
labelsCounts = {}
if numData == 0:
return 0
for featVec in dataset:
currentLable = featVec[-1]
if currentLable not in labelsCounts.keys():
labelsCounts[currentLable] = 0
labelsCounts[currentLable] += 1
gini = 0
for key in labelsCounts:
gini = gini+pow(labelsCounts[key],2)
gini = 1-float(gini)/pow(numData,2)
return gini
def chooseBestFeatureToSplitGini(dataset): #基尼指数
numFeatures = len(dataset[0]) -1 #数据集除去标签后的数据特征个数
baseEntropy = getGini(dataSet) #初始基尼指数
bestInfoGain = 0
bestFeaturn = -1
for i in range(numFeatures):
featList = [example[i] for example in dataset]
uniqueVals = set(featList)
newGini = 0
for val in uniqueVals:
subDataSet = splitDataSet(dataset,i,val) #去除该列的数据集
newGini = newGini + len(subDataSet)*getGini(subDataSet)/len(dataSet)
infoGain = baseEntropy - newGini
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeaturn = i
return bestFeaturn
对比优缺点
ID3算法
主要用于分类问题
优点
在每个节点计算所有特征的信息增益,可能具有较高的计算复杂度。
生成的决策树容易理解和解释。
缺点
ID3对数据的准备性非常敏感,数据中的小变化可能会导致生成完全不同的决策树。
ID3不适用于具有连续属性的数据集,因为连续属性需要事先进行离散化处理。
ID3算法没有内置的机制来防止过拟合,因此生成的决策树可能会对训练数据过拟合。
CART算法
既可以用于分类问题,也可以用于回归问题。
优点
对于分类问题,CART使用基尼不纯度或交叉熵;对于回归问题,使用方差减少或均方误差。
可以自然地处理连续属性,通过选择一个分割点将属性值分为两部分。
可以处理缺失值,为缺失值设计了特定的处理策略。
使用代价复杂度剪枝来控制树的复杂度,减少过拟合的风险。
缺点
由于CART生成的是二叉树,因此可能不如多叉树灵活。
对于大型数据集,CART算法的计算复杂度可能较高。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








