交换瓶子(暴力出奇迹，贪心+置换群）

有 NN 个瓶子，编号 1∼N1∼N，放在架子上。

比如有 55 个瓶子：

2 1 3 5 4

要求每次拿起 22 个瓶子，交换它们的位置。

经过若干次后，使得瓶子的序号为：

1 2 3 4 5
对于这么简单的情况，显然，至少需要交换 22 次就可以复位。

如果瓶子更多呢？你可以通过编程来解决。

输入格式
第一行包含一个整数 NN，表示瓶子数量。

第二行包含 NN 个整数，表示瓶子目前的排列状况。

输出格式
输出一个正整数，表示至少交换多少次，才能完成排序。

数据范围
1≤N≤100001≤N≤10000,

输入样例1：
5
3 1 2 5 4
输出样例1：
3
输入样例2：
5
5 4 3 2 1
输出样例2：
2

 暴力

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e4+10;
int a[N];
ll ans=0;
int main()
{
    int n;cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        int t=i;
        if(t!=a[i])
        {
            for(int j=1;j<=n;j++)
            {
                if(t==j) continue;
                if(t==a[j])
                {
                   swap(a[j],a[t]);
                   ans++;
                }
            }
        }
    }
    cout<<ans<<endl;
    return 0;
    
}

置换群

 

 

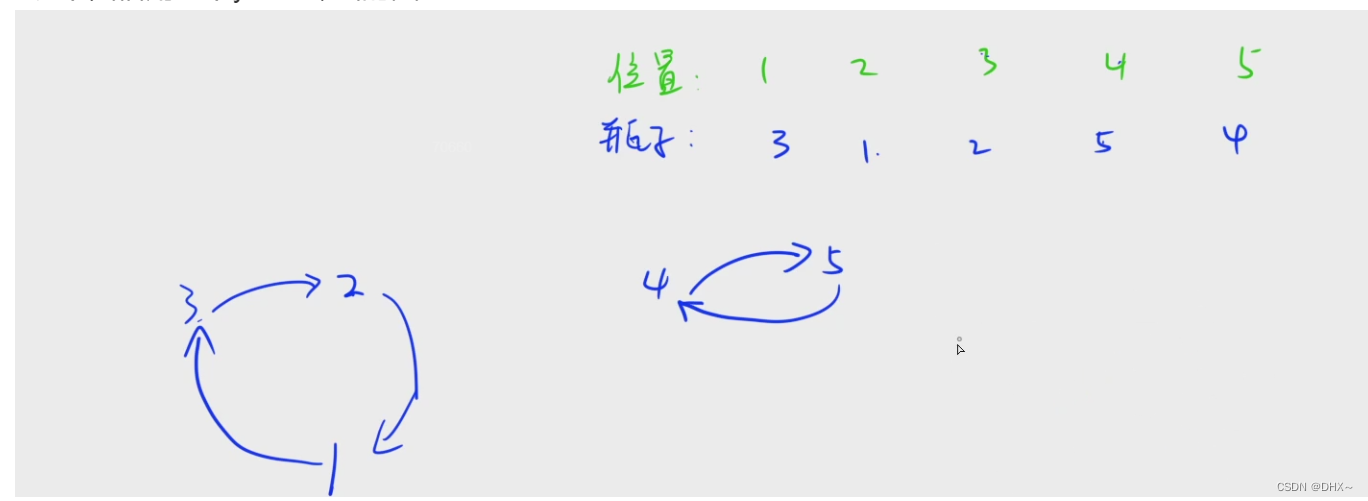
// 交换瓶子
// k个环--> n个环
/*
 情况:
    1. 一个环中的两个节点交换--> 分裂成两个
    2. 两个环中的两个节点交换--> 合成一个环

    k个环--> n个环 (自环)
    最少需要 n-k(只进行情况1)个操作, 所以答案就是n-k
 */
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e4+10;
bool st[N];
int a[N];
int main()
{
    int n;cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    ll ans=0;//环的数量
    for(int i=1;i<=n;i++)
    {
        if(!st[i])//如果没有被标记过，就说明这个点在一个新的环中
        {
            ans++;//环++
            for(int j=i;!st[j];j=a[j])
            {
                st[j]=true;//走完这个环 每次变更指向a[j] 即瓶子初始序号的第j个
             // 1 2 3 4 5
            // 3 1 2 5 4
            // 3指向2  j=a[3]=2
            // 2指向1  j=a[2]=1
            // 1指向3  j=a[1]=3;
            // 3指向2  j=a[3]=2 -->被标记过了
            // st[2]   st[3]
            // st[4] st[4]=true  4指向5 j=a[4]=5
            //       st[5]=true  5指向4 j=a[5]=4;
            // 一共两个环
            }
        }
    }
    cout<<n-ans<<endl;
    return 0;
}