汉诺塔问题

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

问题描述：有三根柱子，分别为 A、B、C，A 柱子上有 n 个盘子，盘子大小不一，大盘子在下，小盘子在上。现在需要将 A 柱子上的所有盘子移动到 C 柱子上，每次只能移动一个盘子，且大盘子不能放在小盘子上面。在移动过程中可以使用 B 柱子作为中转站。

 代码段

#include<iostream>
using namespace std;
 
void hanoi(int paraN, char paraSource, char paraDestination, char paraTransit) {
	if (paraN <= 0) {
		return;
	}
	else {
		hanoi(paraN - 1, paraSource, paraTransit, paraDestination);
		cout << paraSource << " -> " << paraDestination << endl;
		hanoi(paraN - 1, paraTransit, paraDestination, paraSource);
	}//of if
}//of hanoi
 
/*
* Test the hanoi.
*/
void hanoiTest() {
	cout << "---- addTOTest begins. ----" << endl;
 
	cout << "2 plates" << endl;
	hanoi(2, 'A', 'B', 'C');
 
	cout << "3 plates" << endl;
	hanoi(3, 'A', 'B', 'C');
 
	cout << "---- addToTest ends. ----" << endl;
}
 
/*
* The entrance
*/
void main() {
	hanoiTest();
}

运行结果

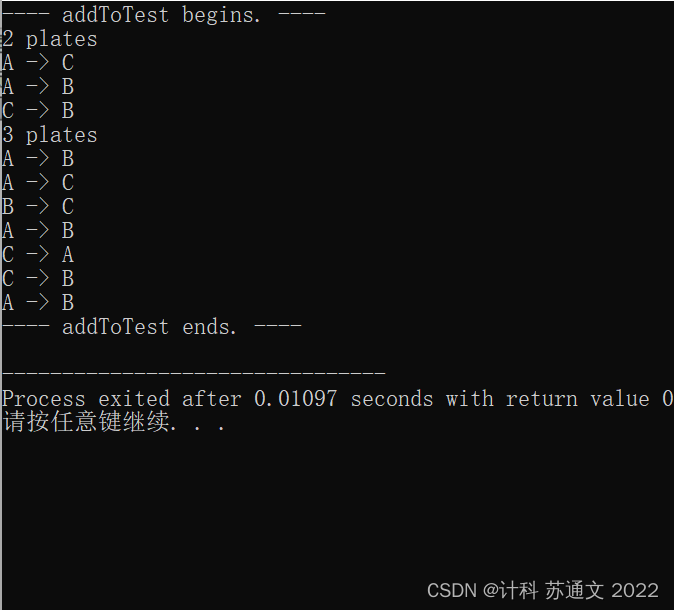
对于汉诺塔问题的分析：

自顶向下，逐渐求精：汉诺塔问题的解决方式是自顶向下逐渐求精。首先，我们需要将最上面的圆盘移动到第三个柱子上，然后将剩余的圆盘移动到第二个柱子上，最后将最上面的圆盘移动到第二个柱子上。因此，这个问题可以分解为三个子问题，即将 n-1 个圆盘从第一个柱子移动到第二个柱子，将第 n 个圆盘从第一个柱子移动到第三个柱子，再将 n-1 个圆盘从第二个柱子移动到第三个柱子。这三个子问题可以分别递归解决，最终得到整个问题的解。

函数调用、递归和分治：为了解决汉诺塔问题，我们需要使用函数调用、递归和分治。具体来说，我们可以编写一个函数 hanoi(n, a, b, c)，其中 n 表示要移动的圆盘数，a、b 和 c 分别表示三个柱子。该函数首先检查 n 的值，如果 n == 1，则直接将圆盘从柱子 a 移动到柱子 c；否则，该函数会将问题分解为三个子问题，并递归调用 hanoi() 函数来解决这些子问题。

形参与实参：在函数调用过程中，我们使用形参来表示函数的输入参数，而实参则是在函数调用时提供的具体数值。在汉诺塔问题中，形参 n、a、b 和 c 分别表示要移动的圆盘数和三个柱子。在函数调用时，我们需要提供实际的圆盘数和三个柱子的具体名称，如 hanoi(3, ‘A’, ‘B’, ‘C’)。

有意义、规范的标识符：在编写程序时，使用有意义、规范的标识符可以使代码更易于理解和维护。在汉诺塔问题中，我们可以使用有意义的变量名和函数名，如 n、a、b、c 和 hanoi()。这些标识符可以更好地表达程序的含义，并提高代码的可读性。

时间复杂度：汉诺塔问题的时间复杂度为 O(2^n)，其中 n 是圆盘的数量。这是因为在每次递归调用中，我们需要移动 2 个圆盘。此外，在解决汉诺塔问题的过程中，我们需要进行 n 次递归调用，每次递归调用需要进行 3 次移动操作。因此，总的移动次数为 3^(n - 1)，这是一个指数级别的复杂度。在实际应用中，当圆盘数量较大时，解决汉诺塔问题的时间复杂度会变得非常高。

递归栈：递归函数的调用过程需要使用递归栈来保存每个函数调用的状态。在汉诺塔问题中，每个递归调用会创建一个新的函数调用帧，并将其压入递归栈中。当递归调用返回时，对应的函数调用帧会被弹出，恢复到上一层调用的状态。因此，在解决汉诺塔问题的过程中，递归栈的深度等于递归调用的层数，即 n。

空间复杂度：汉诺塔问题的空间复杂度为 O(n)，其中 n 是圆盘的数量。这是因为在解决问题的过程中，我们需要使用一个递归栈来保存每个递归调用的状态。由于递归栈的深度等于递归调用的层数，因此空间复杂度为 O(n)。除了递归栈之外，我们还需要使用一些额外的变量来保存问题的状态，但这些变量的数量与圆盘的数量无关，因此不会影响空间复杂度。

总之，汉诺塔问题涉及到自顶向下的逐渐求精、函数调用、递归和分治。通过合理地使用形参和实参、有意义、规范的标识符和递归栈，我们可以解决这个问题，并计算出它的时间复杂度和空间复杂度。

递归法:解决该问题的思路需要用到一种比较重要的算法：递归算法(即函数自己调用自己本身)

当 n = 1 时，直接将盘子从 A 柱子上移到 C 柱子上即可。

当 n > 1 时，将问题分解为三个子问题：

将 A 柱子上的前 n-1 个盘子移到 B 柱子上；

将 A 柱子上的最后一个盘子移到 C 柱子上；

将 B 柱子上的 n-1 个盘子移到 C 柱子上。

对于子问题 1 和 3，可以采用同样的方法进行递归求解，直到 n=1 时停止递归。