最大流算法（FF,EK,Dinic）

网络模型的建立

可以把网络想象成一堆相互联通的水管，水能通过某个管道到达另一个管道，每个管道有容量限制，即每个管道只能通过一定流量的水，既然是水管网络，那么一定有进水口，和出水口。把进水口记作源点S，出水口记作汇点T，而最大流问题探究的就是从源点到汇点的最大流量.

将从点U流向点V的流（flow） 记作 F_u→v
将从点U连向点V的管道容量 记作 C_u→v

对于所有合法的流有 F_u→v <= C_u→v

引出残量网络 记 R_u→v = C_u→v – F_u→v

最大流问题

思考

对于求解该问题，我们先从使得从源点流入汇点的流量最大入手，对于给出的网络，我们进行可行边的找寻，这里的可行边指的是R（残量）大于0的边，如果存在一条从源点出发到达汇点的可行路径，就对该路径进行拓展，根据木桶原理，该路径流通的最大流量为该路径上最小的R

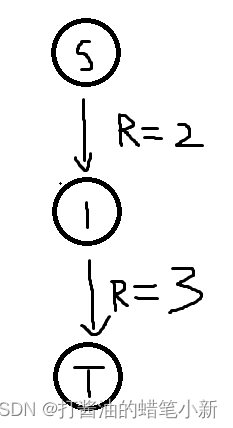
如图在该有效路径中，最小的R为2，所以该路径可以流通2的流量，在流通后应当对残量网络进行更新

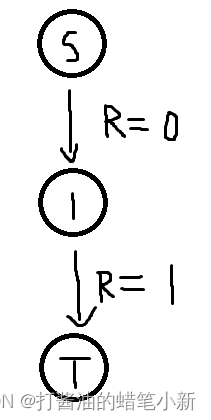
通过一直寻找可行路径，并对其进行拓展能增大总流量，当没有从s到t的可行路径时，结束寻找。

上面的方法是能直观想到增大总流量的朴素方法，但此方法求出的总流量真的是最大流吗？
考虑下述情况

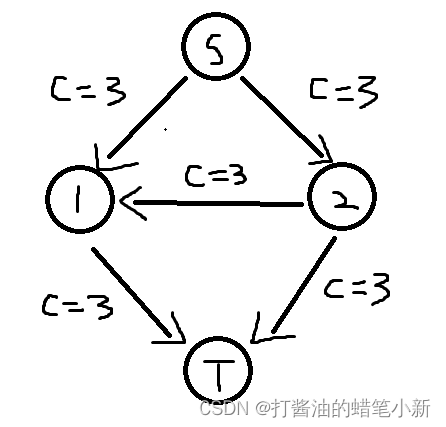
如果在寻找可行路径时，找到了 S→2→1→T的路径，可知其最大流量为3，更新残量网络

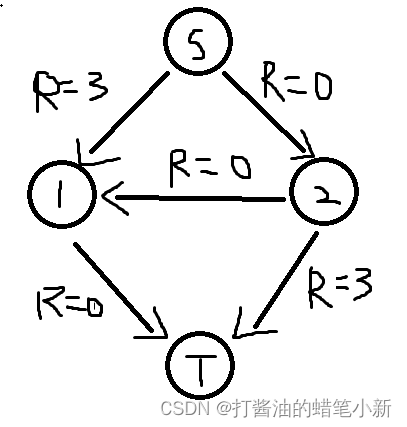
此时在进行拓展，发现没有从S到T的可行路径，结束寻找，此时总流量为3，而可以直接看出最大流应该为 6
于是我们知道拓展路径的顺序可能会对答案产生影响，那么有没有方法可以消除这种影响呢？

Ford-Fulkerson算法

算法思想

该算法（后文简称为FF算法）是基于上面的朴素方法的改进，在每次拓展时，对可行路径上的边添加了一条反边。
以上文中的例子为例，在更新残量网络时添加了反边

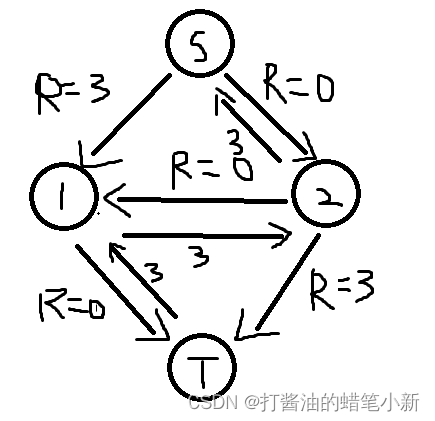
反边上的残量为正向边的流量 即：
R_v→u = F_u→v
于是在后续寻找可行路径时能够借助该反向边达到一种类似于反悔的退流效果。

退流操作并没有凭空产生新的流量，当需要用到退流操作时，一定有一条新的可行路径流入了退流操作同样大小的流量，相当于第二次拓展产生的流和第一次拓展产生的流相互抵消，这种反悔操作让我们无需担心上文提到的顺序问题

以上图为例，该图的下一次拓展有从 S→1→2→T的可行路径
更新残量网络后如图

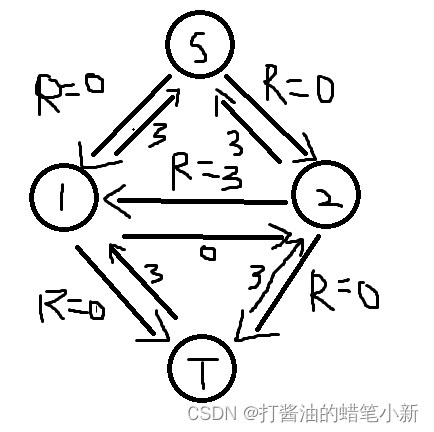
此时流出的总流量为6，并且在图中没有新的可行路径，最大流求解成功

关于时间复杂度

每次查找可行路径的时间复杂度为O（E），每轮更新总流量都会增加，设最大流为 F，总共更新的次数不超过F轮，所以总的时间复杂度为O（FE）

Edmond—Karp 算法

EK算法是基于FF算法的改进，EK算法要求FF算法在进行找寻可行边操作时使用bfs操作。

时间复杂度

EK算法的时间复杂度为O（VE²）关于证明请参考 oiwiki

代码实现

#include <stdio.h>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
int head[N],nex[N],to[N],pre[N],vis[N],cnt=1,n,m,s,t;
// cnt初始化为1，保证正反边cnt异或值为1
ll val[N],dis[N],ans;
int bfs(){
	queue<int>q;
	for(int i=1;i<=n;++i) vis[i]=0;
	q.push(s);//将源点加入队列
	dis[s]=0x3f3f3f3f3f3f3f3f;
	vis[s]=1;
	while(q.size()){
		int x=q.front();
		q.pop();
		if(x==t) return 1;//如果x==t说明找到可行路径了
		for(int i=head[x];i;i=nex[i]){
			int k=to[i];
			if(vis[k]||val[i]==0) continue;//如果遍历过或者该边权值为0了就无法进行增广了
			pre[k]=i;//记录每个点的前一条边，方便修改答案
			dis[k]=min(dis[x],val[i]);//记录每条路径上的最小容量
			vis[k]=1;
			q.push(k);
		}
	}
	return 0;
}
void add(int x,int y,ll k){
	nex[++cnt]=head[x];
	to[cnt]=y;
	val[cnt]=k;
	head[x]=cnt;
}
void update(){
	int x=t;
	while(x!=s){
		int i=pre[x];
		val[i]-=dis[t];//正向边权值减去流量
		val[i^1]+=dis[t];//反向边权值加上流量
		x=to[i^1];
	}
	ans+=dis[t];//更新答案
}
int main(){
	cin>>n>>m>>s>>t;//输入n点数，m边数，s源点，t汇点
	for(int i=1;i<=m;++i){
		int x,y;
		ll k;
		cin>>x>>y>>k;
		add(x,y,k);//添加正向边
		add(y,x,0);//使用链式前向星建反边
		//正反边的cnt异或为1，方便对正反边权值进行修改
	}
	while(bfs()){//当有可行路径时继续增广
		update();//对每条可行路径的权值进行更新，更新答案
	}
	cout<<ans;
	return 0;
}

Dinic算法

算法思想

EK和FF算法每次只能增广一条可行路，能不能一次增广多条可行路呢？
Dinic算法就是对此的改进，通过将原图分层的方法，它可以支持一次bfs增广多条可行路径

时间复杂度

Dinic算法的时间复杂度为O（V²E） 证明请参考oiwiki

代码实现

#include <stdio.h>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f3f3f3f3f;
int head[N],to[N],nex[N],cnt=1,n,m,now[N],dis[N];
ll val[N],ans,num;
void add(int u,int v,ll k){
	nex[++cnt]=head[u];
	to[cnt]=v;
	val[cnt]=k;
	head[u]=cnt;
}
int bfs(){
	for(int i=1;i<=n;++i) dis[i]=0;
	dis[1]=1;
	queue<int>q;
	q.push(1);
	while(q.size()){
		int x=q.front();
		q.pop();
		now[x]=head[x];//当前弧优化
		if(x==n) return 1;
		for(int i=head[x];i;i=nex[i]){
			int k=to[i];
			if(dis[k]||val[i]==0) continue;//如果该点已经分层，或该边权值已经为0了就跳过
			dis[k]=dis[x]+1;//该点的层级为上一节点层级＋1
			q.push(k);
		}
	}
	return 0;
}
ll dfs(int x,ll sum){//sum维护一条路径上的最小容量
	if(x==n) return sum;//如果x==t 返回该路径上的最小容量
	ll k,res=0;//res为该点的总流出量
	for(int i=now[x];i;i=nex[i]){
		now[x]=i;//当前弧优化，如果一条边在其他路径上已经使用过并且以无法增广时在下次遍历该点时应当跳过这些边
		int v=to[i];
		if(dis[v]!=dis[x]+1||val[i]==0) continue;
		k=dfs(v,min(sum,val[i]));// k是这条路径上的最小容量
		if(k==0) dis[k]=inf;//如果k==0可知k点已经无法向汇点进行增广了，此时应将k点从分层图中踢出
		val[i]-=k;//正向边减去流量
		val[i^1]+=k;//反向边加上流量
		res+=k;//该点的总流量加上k
		sum-=k;//该点之前的最小容量减去k
	}
	return res;//返回该点总流量，代表上一个点能通过该点流出的总流量
}
int main(){
	cin>>m>>n;
	for(int i=1;i<=m;++i){
		int u,v;
		ll k;
		cin>>u>>v>>k;
		add(u,v,k);
		add(v,u,0);
	}
	while(bfs()){//将图进行分层
		ans+=dfs(1,inf);
	}
	cout<<ans;
	return 0;
}