数据结构面试高频题

1、数据结构是什么？数据结构的三要素是什么？

数据结构是计算机中存储、组织数据的方式，它定义了数据元素之间的关系以及操作这些数据的方法。

数据结构的三要素是：逻辑结构、存储结构和数据的运算。逻辑结构指的是数据元素之间的逻辑关系，分为线性结构（线性表、栈、队列、串、数组）和非线性结构（集合、树、图）。存储结构指的是数据在计算机中的具体存储方式，分为顺序存储、链式存储、索引存储、哈希存储。数据的运算，指对数据结构上进行的基本操作，如插入、删除、查找、遍历等。

2、时间复杂度和空间复杂度是什么？怎么计算？

时间复杂度表示算法执行所需的基本操作次数，空间复杂度表示算法运行过程中所需的额外存储空间大小。

时间复杂度计算：统计基本操作的执行次数（通常是循环的最深层），去除低阶项和常系数，保留最高阶，采用大O表示法。

空间复杂度计算：分析算法中定义的变量、数组、递归栈等所占空间，取最主要部分，使用大O表示。

3、顺序存储和链式存储的区别

顺序存储（如顺序表）将元素保存在一块连续的内存空间中，支持随机访问，但插入和删除的效率较低。

链式存储（如链表）通过指针将元素连接在一起，内存使用灵活，插入和删除操作的效率高（但注意不一定是O(1)，因为还需要进行元素查找），但只能顺序访问，需要从头逐结点遍历。

4、头指针和头结点的区别？引入头结点的优点？

不管是否有头结点，头指针始终指向链表的第一个结点；而头结点是带头结点的链表中的第一个结点，结点中通常不存储数据，头结点的指针域指向链表的第一个元素结点。

优点：由于第一个数据结点的位置被存放在头结点的指针域中，因此在链表的第一个位置上的操作和在表的其他位置上的操作保持一致，不需要进行特殊处理。
此外，无论链表是否为空，其头指针都是指向头结点的非空指针，因此空表和非空表的处理也得到了统一。

5、如何判断链表是否有环？

设置两个指针，快指针每次走两步，满指针每次走一步。如果链表无环，快指针最终会走到NULL；如果链表有环，快慢指针最终会在环内相遇。

6、栈和队列的区别

栈和队列都是操作受限的线性表。

栈是先进后出的数据结构，只能在一端进行插入和删除，称为栈顶，常用于表达式求值、括号匹配等场景。

队列是先进先出的数据结构，插入操作在队尾，删除操作在队头，常用于缓冲处理、广度优先搜索等场景。

7、简要介绍共享栈

共享栈是一种节省空间的栈结构，它在一块连续的内存空间中同时存放两个栈，一个栈从低地址向上增长，一个栈从高地址向下增长，当两个栈的栈顶指针相遇时表示栈满。共享栈能有效提高内存利用率，适合两个栈交替使用、空间需求动态变化的场景。

8、如何区分循环队列是队空还是队满？

方法一（最常用）：预留一个空的存储单元：当front == rear时，表示队列为空；当(rear+1)%maxSize==front时，表示队列为满。

方法二：增设表示元素个数的size。当有元素入队时，size++；当有元素出队时，size–。这样，队空的条件为size=0；队满的条件是size=maxSize。

方法三：增设tag，用来表示当前操作是入队还是出队，tag=false表示出队，tag=true表示入队。当front == rear，且tag=false时，表示队空；当front == rear，且tag==true时，表示队满。

9、介绍一下栈在括号匹配中的应用

遇到左括号就入栈；遇到右括号则判断栈顶是否为匹配的左括号，若匹配则出栈，否则匹配失败；遍历结束后，若栈为空，则括号匹配成功，否则失败。

10、简要介绍一下栈在中缀表达式转后缀表达式中的应用

遇到操作数直接输出；遇到运算符则与栈顶比较优先级，若优先级不高于栈顶则弹出栈顶运算符并输出，直到遇到优先级低的、左括号、栈空，然后再入栈当前运算符；遇到左括号直接入栈，遇到右括号则弹出直到遇到左括号为止；最终将栈中剩余的运算符依次输出即可得到后缀表达式。

11、介绍栈在后缀表达式求值的应用

从左到右依次扫描后缀表达式，遇到操作数，将其压入栈中；遇到操作符，从栈中弹出两个操作数，进行运算，并将结果重新入栈；表达式遍历完成后，栈顶元素即为表达式的最终结果。

12、简要介绍一下KMP算法

KMP算法是一种高效的字符串匹配算法，用于在一个主文本串中快速查找一个模式串的所有出现位置。

它的核心思想是当出现字符不匹配时，利用已经匹配成功的部分信息，避免将模式串从头开始重新匹配，而是通过一个预先计算好的“部分匹配表”（也称为next数组）将模式串向后滑动尽可能远的距离，从而将时间复杂度从暴力算法的O(m*n)优化到O(m+n)，极大地提高了匹配效率。

next数组的核心是模式串的自我匹配。它存储的是模式串中每个位置之前的子串中，其最长相等前后缀的长度。

具体求解时，可以用两个指针（或下标）i 和 j 来动态规划：
i 指向当前需要计算next值的位置（后缀的末尾）。
j 指向前缀的末尾，同时也代表当前 i 之前子串的最长相等前后缀的长度。

算法的过程是：初始化后，通过比较 i 和 j 位置的字符，来不断调整 j 的位置（回退），直到匹配成功或 j 回到开头，从而确定 next[i] 的值。这个过程确保了高效的计算。

13、满二叉树和完全二叉树的区别是什么？

满二叉树是指一棵二叉树中，除叶子结点之外的每个结点都有两个子结点，并且所有叶子结点都在同一层，其结构最饱满、对称，结点总数一定是2^h-1。

完全二叉树则要求除了最后一层外，其余各层的结点数都必须达到最大值，并且最后一层的结点必须是从左到右连续排列的，但可以缺少部分右侧结点。满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

14、什么是线索二叉树？

线索二叉树是一种对二叉树进行改造的存储结构。在普通二叉树中，很多结点的左右指针是空的，这些空指针并没有被利用。线索二叉树就是利用空指针加上线索标志，将二叉树结点在遍历序列中的前驱和后继信息存储起来的二叉树。能够提高二叉树遍历的效率，减少空指针的浪费。

15、简述哈夫曼树和哈夫曼编码

哈夫曼树是一种带权路径长度最短的二叉树，常用于数据压缩领域，比如哈夫曼编码。

哈夫曼树的构造过程：将所有权值看作是一棵棵单结点树，放入优先队列；取出权值最小的两棵树作为左右子树，合并成一棵新的树，权值为两者之和；将新树插入到优先队列；；重复上面的操作，知道队列中只剩下一棵树，即为哈夫曼树。

哈夫曼编码是一种基于哈夫曼树的无损数据压缩的编码方法，它利用字符出现的频率来设计编码，使得出现频率高的编码短，出现频率低的编码长，从而达到整体长度最短的效果。

哈夫曼编码的编码过程：根据字符的权重构建哈夫曼树；从根节点到每个叶子结点的路径上，规定向左走编码为"0"，向右走编码为"1"；每个字符对应路径上的"0"和"1"组成它的哈夫曼编码。

16、简要介绍一下图的几种存储方式

邻接矩阵：用二维数组表示，适合稠密图，判断两点是否相连快

邻接表：每个顶点有一个链表存相邻结点，适合稀疏图

邻接多重表（无向图）：边作为结点，每条边记录两个顶点基于这两个顶点相邻的下一条边的指针

十字链表（有向图）：边结点同时连接两个顶点的相关链表，方便删除或者查找边，结构较复杂

17、简要介绍一下BFS和DFS

BFS：按层次遍历，从起始点开始，先访问相邻顶点，再依次访问更远的顶点；通常用队列实现，适合求无权图最短路径和层次结构。

DFS：尽可能深入访问未访问的顶点，直到无路可走再回溯；通常用递归或栈实现。适合求连通分量、拓扑排序等。

18、最小生成树是什么？有哪些算法？

在一个连通加权无向图中，包含所有顶点，边数为n-1，并且总权值最小的生成树为最小生成树。

Prim算法：
思想：属于贪心算法。从一个任意顶点开始，逐步“长大”生成树。在每一步，总是选择一条连接当前生成树与树外顶点的权重最小的边，并将该顶点和边加入生成树。
适用场景：更适合于边稠密的图。

Kruskal算法：
思想：也属于贪心算法。它不考虑树的结构，而是将所有边按权重从小到大排序，然后依次考察每条边。如果加入当前边不会与已选择的边形成环，就将其加入生成树，否则跳过。
实现关键：通常使用并查集数据结构来高效判断是否形成环。
适用场景：更适合于边稀疏的图。

19、最短路径算法有哪些？

Dijkstra算法：解决单源最短路径问题（从一个源点到其他所有顶点的最短路径）。

要求：图中边的权重不能为负数。
思想：贪心算法。它按路径长度递增的顺序逐步确定最短路径。
具体操作：略

Floyd（弗洛伊德）算法：解决多源最短路径问题（图中任意两点之间的最短路径）。
特点：是一个动态规划算法，思想直接，通过三重循环不断松弛更新任意两点间的距离。
具体操作：略

20、简要介绍二叉排序树和二叉平衡树

二叉排序树（BST，也叫二叉搜索树）：它是一棵二叉树，并且满足以下性质：对于树中任意节点，其左子树上所有节点的值都小于该节点的值；其右子树上所有节点的值都大于该节点的值。
目的：为了实现数据的快速查找、插入和删除（平均时间复杂度为O(log n)）。

二叉平衡树（AVL树）：它首先是一棵二叉排序树，并且附加了一个严格的平衡条件：任意节点的左子树和右子树的高度差（平衡因子）的绝对值不超过1。
目的：为了解决二叉排序树在极端情况下（如插入有序序列）会退化成链表，导致性能下降为O(n)的问题。通过旋转操作（左旋、右旋）来维持平衡，保证了查询、插入、删除操作的最坏时间复杂度也是O(log n)。

21、说说红黑树与平衡二叉树有什么区别？

红黑树是一种自平衡的二叉搜索树，通过给节点着色并满足特定性质，保证书的高度近似平衡，从而支持O(logn)的查找、插入和删除操作。满足"左根右，根叶黑，不红红，黑路同"。

与平衡二叉树相比：
平衡要求：平衡二叉树更严格，要求左右子树高度差最多为1；红黑树平衡条件较松，从根节点到叶节点的最长路径不大于最短路径的二倍即可。
调整成本：平衡二叉树插入和删除后可能需要多次旋转调整；红黑树调整相对较少，插入删除更快。
查找效率：平衡二叉树通常查找更快；红黑树更适合频繁插入删除的场景。

简单来说，平衡二叉树追求更严格的平衡，红黑树在保持平衡的同时更注重操作效率。

22、简单介绍一下B树和B+树，说说二者的区别

（1）B树：
引入原因：由于传统二叉树的结点较小，频繁访问导致大量磁盘IO，效率低下。B树通过增加每个结点的容量，减少树的高度和访问次数，从而大幅降低磁盘读写，提高查找和更新频率。

介绍：B树是一种多路平衡搜索树，广泛用于数据库和文件系统中，适合存储大量数据。它的每个结点可以有多个子结点，结点中存储多个关键字，保证所有叶子结点在同一层，树的高度较低，支持高效的查找、插入和删除操作，时间复杂度为O(logn)。

（2）B+树：
引入原因：由于B树每个节点存放数据，而数据相比关键字占用的空间较大，会导致每个磁盘块存放的索引项的记录会变少。B+树的非叶子节点不存放数据，只存放指针和关键字，这样每个磁盘块就可以存放更多的记录。这样深度会减小很多，加快了IO速度。

介绍：B+树是B树的变种，所有数据都存储在叶子节点，非叶子节点只存储索引键。叶子节点通过指针形成链表，方便范围查询和顺序遍历。仍保持多路平衡，树高低，查找效率高。

应用：在文件系统中，B+树通常用于管理磁盘上的文件块和索引节点。在数据库中，B+树常被用作索引结构，用于快速查找和排序大量数据，入主键索引、唯一索引、辅助索引等。

（3）B树和B+树的区别：

数据存储位置：B树的关键字和数据都存储在内部节点和叶子节点；B+树的数据只存储在叶子节点，内部节点仅存储索引键。

叶子结点结构：B树的叶子节点没有指针连接；B+树的叶子节点通过链表相连，方便范围查询和顺序访问。

查询效率：B树的范围查询效率较低；B+树因为所有数据都在叶子节点，且叶子链表支持顺序遍历，范围查询更高效。

树的高度：在相同数据量下，B+树的内部节点只存索引，通常能存储更多索引键，树高更低，查找更快。

分叉个数：B树分叉个数等于关键字个数+1，B+树分叉个数等于关键字个数。

23、介绍一下哈希表，如何构造哈希函数，如何解决哈希冲突

（1）哈希表（散列表）是一种通过键值（Key） 直接进行访问的数据结构。它通过一个哈希函数将Key映射到表中的一个位置来访问记录，从而实现平均情况下接近O(1)时间复杂度的查找、插入和删除。

（2）构造哈希函数的方法：目标是让key均匀分布到地址空间。

直接定址法：Hash(Key) = a * Key + b。简单、均匀，但需要事先知道key的分布。
除留余数法：最常用。Hash(Key) = Key % p（p通常取一个素数或不被小于20的质数整除的数，以减少冲突）。
数字分析法：抽取key中的部分数字作为地址，适用于key位数较多且已知分布。
平方取中法：将key平方后，取中间的几位作为地址。

（3）解决哈希冲突的方法：

当不同的key被映射到同一个地址时，就发生了冲突。解决方法主要分为两类：

开放定址法：如果发生冲突，就寻找下一个空的哈希地址。包括：线性探测：顺序地往后查找空位；二次探测：以二次方为间隔进行探测。

链地址法（拉链法）：最常用。将哈希到同一地址的所有元素都放在一个链表中。HashMap就采用这种方法。这样，哈希表的主体是一个数组，而每个数组元素是一个链表的头指针。

24、介绍三种插入排序的基本思路

直接插入排序：这是最基础的形式。它从数组的第二个元素开始，将其与前方已排序的元素从后向前逐个比较，找到合适的位置后，将其插入。这个过程需要逐个后移元素来空出插入位。

折半插入排序：在直接插入排序的基础上，采用二分查找在已排序的序列中找到插入位置，减少比较次数。

希尔排序（最小增量排序）：将整个数组分成若干子序列，分别进行直接插入排序，逐步缩小序列间隔，最后整体排序。通过初期大跨度排序，使得数组局部有序，提高整体效率。

25、介绍两种交换排序的基本思路

冒泡排序：核心思路是重复地遍历序列，依次比较相邻的两个元素。如果它们的顺序错误（例如，前一个比后一个大），就交换它们。这样，每一轮完整的遍历都会将当前未排序部分中的最大（或最小）元素“浮”到其最终的正确位置，就像气泡从水底冒到水面一样。这个过程重复进行，直到整个序列有序。

快速排序：选取一个基准元素，通过划分操作将数组分为两部分，左边部分都比基准小，右边部分都比基准大；然后，递归地对基准元素前后两个子序列重复上述过程。

26、介绍两种选择排序的基本思路

简单选择排序：每次从未排序的部分中选出最大或最小的元素，放到已排序部分的末尾；重复此过程，直到整个数组有序。

堆排序：利用堆这种数据结构，现将数组建成一个最大堆或最小堆；然后将堆顶元素与末尾元素交换，缩小堆的大小，重新调整堆，保证堆性质；重复此过程，最终得到有序序列。

27、介绍一下归并排序

归并排序是一种典型的分治算法，基本思路是将数组不断递归地分成两半，分别排序后再合并成一个有序序列。
分解：将待排序序列分成两个长度大致相等的子序列；
递归排序：对这两个子序列分别递归调用归并排序；
合并：将两个已排序的序列合并成一个有序序列。

28、介绍一下基数排序

基数排序是一种非比较型的整数排序算法，按数字的位数逐位排序，常用于对整数或固定长度字符串的排序。
将所有待排序的元素按最低为进行排序，保证排序稳定；依次对更高位进行排序，直到最高位完成排序；每一轮排序都是有稳定的排序方法，确保前一位的顺序不被破坏。
适合数据位数不多且范围确定的场景。

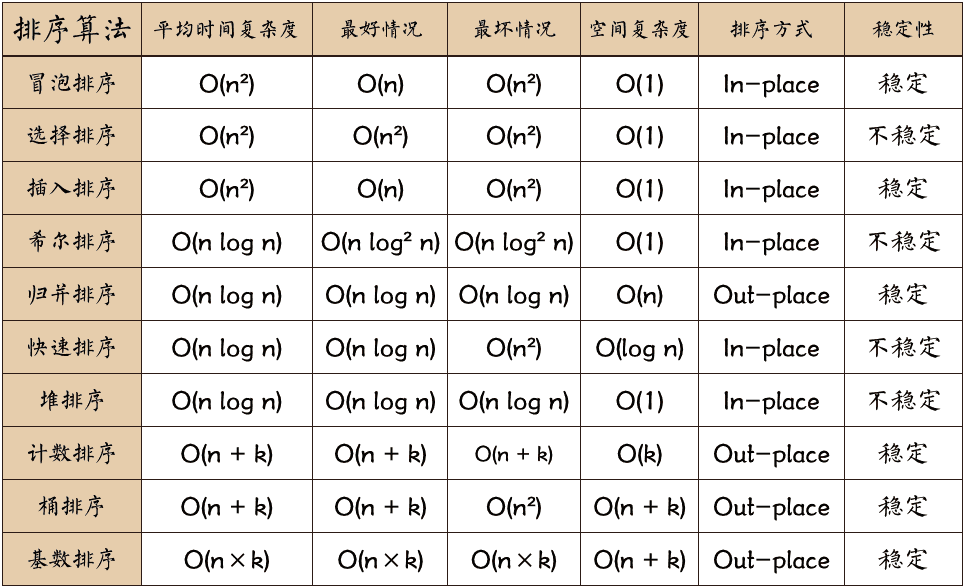
29、各种排序算法的性能、稳定性、时间复杂度、空间复杂度