主成分分析（PCA）原理详解

相关背景
在许多领域的研究和实际应用中，为了深入理解事物的本质和寻找潜在规律，研究者们经常需要对多个变量进行大量的观测和数据收集。这些多变量大样本的数据集虽然为分析提供了丰富的信息基础，但同时也带来了数据采集的高工作量和数据处理的复杂性。特别是当这些变量之间存在一定程度的相关性时，问题分析的难度会显著增加，因为单独分析每个指标往往难以提供全面而综合的见解。
 因此需要找到一个合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系，因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析与因子分析就属于这类降维的方法。

PCA降维实例
假设我们有一个包含四个二维数据点的数据集，数据点如下：

A(1, 2)
B(2, 3)
C(3, 1)
D(4, 2)
这些点分布在二维平面上，但我们的目标是使用PCA降维方法将它们映射到一条直线上，从而实现从二维到一维的降维。

以下是PCA降维的详细步骤：

1.数据预处理：
首先，我们需要将原始数据按列组成矩阵X。在本例中，矩阵X为：
1 2  
2 3  
3 1  
4 2
接着，对X矩阵的每一行进行零均值化，即减去该行的均值。计算得到每行的均值分别为2、2.25、2、2.5，零均值化后的数据为：
-1       0  
-0.25  0.75  
1         -1  
1.5      -0.5
2.求协方差矩阵及其特征值和特征向量：
计算零均值化后的数据的协方差矩阵C。在本例中，C为：
0.6875  0.3125  
0.3125  0.6875
接着，求解协方差矩阵C的特征值和特征向量。特征值λ1和λ2分别为1和0.375，对应的特征向量v1和v2分别为[0.707, 0.707]和[-0.707, 0.707]（已归一化）。
3.选择主成分并构建新的坐标系：
选择特征值较大的特征向量作为新的坐标系的基向量。在本例中，我们选择λ1对应的特征向量v1作为新的坐标系的基向量。
数据降维：
将原始数据投影到新的坐标系上，即计算原始数据与基向量的点积，得到降维后的数据。在本例中，降维后的数据为原始数据矩阵与v1的点积，即：
[-1 * 0.707 + 0 * 0.707, ...] = [-0.707, ...]  
[-0.25 * 0.707 + 0.75 * 0.707, ...] = [0.4607, ...]  
[1 * 0.707 + (-1) * 0.707, ...] = [0, ...]  
[1.5 * 0.707 + (-0.5) * 0.707, ...] = [0.707, ...]
由此，我们得到了降维后的一维数据：[-0.707, 0.4607, 0, 0.707]。
结果解释：
通过PCA降维，我们将原始二维数据成功降维到一维，同时尽可能地保留了数据中的主要信息。在这个例子中，新的一维数据可以看作是原始数据在最大方差方向（即主成分）上的投影。
通过上述实例，我们可以清晰地看到PCA降维的过程和效果，以及它在简化数据表示、降低计算复杂性方面的作用。

PCA推导
首先，我们考虑一个二维的场景，这里仅涉及两个变量，它们分别由横坐标和纵坐标来代表。因此，每个观测值都在这两个坐标轴上具有相应的坐标值。如果这些数据在二维平面上形成了一个椭圆形状的点阵，这个椭圆具有一个长轴和一个短轴。

观察椭圆形状的点阵，我们可以看到在短轴方向上，数据的变化幅度非常小。如果短轴退化到几乎成为一个点，那么只有长轴方向上的变化才能显著地解释这些点的变动情况。在这种情况下，从二维降到一维的降维过程就变得非常自然和直观了。

具体来说，当我们考虑这个椭圆时，PC1代表了主成分方向，它是长轴的方向。而在二维空间中，与PC1方向正交的方向就是PC2的方向，即短轴的方向。如果我们沿着PC1轴（也就是主成分方向）观察这些数据，会发现数据在这个方向上的离散程度最大，也就是说方差最大。这意味着数据在PC1轴上的投影包含了原始数据的绝大部分信息，即使我们忽略了PC2轴（短轴）上的信息，也不会损失太多有用的信息。

此外，PC1和PC2这两个方向是不相关的，它们正交于彼此。因此，当我们只考虑PC1方向时，实际上就是将二维数据降维到了一维。这种降维方法特别适用于椭圆的长短轴相差较大的情况，因为此时大部分信息都集中在长轴上，而短轴上的信息相对较少，因此降维的合理性更高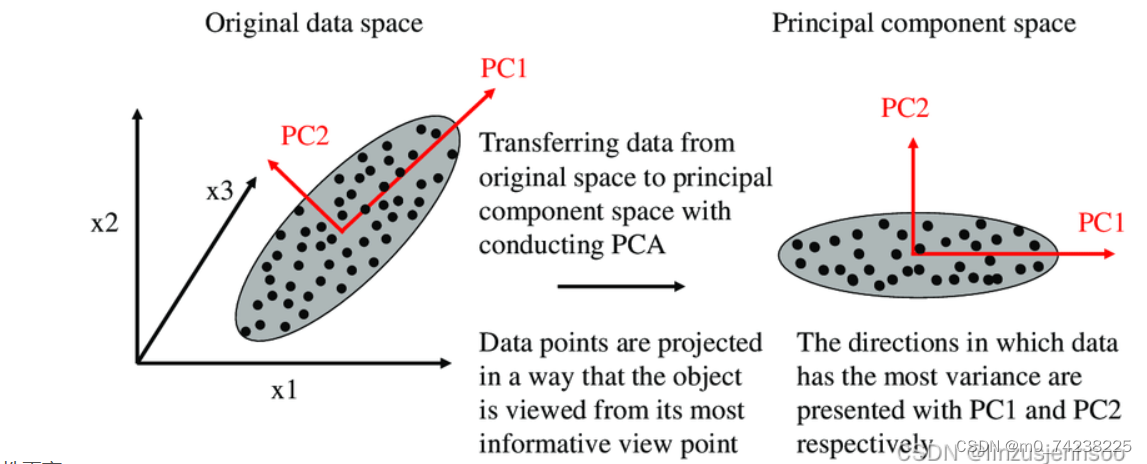


 

1. 最大方差理论
在信号处理中，我们通常认为信号本身具有较大的方差，而噪声则具有较小的方差。信噪比（SNR）是一个重要的度量，它表示信号与噪声的方差之比，并且这个比值越大，说明信号的质量越好，噪声的影响越小。

当我们考虑将n维样本点转换为k维特征时，我们希望转换后的每一维特征都能尽可能多地保留原始信号的信息，同时减少噪声的影响。根据方差最大化理论，一个好的k维特征空间应该使得样本点在这些维度上的投影具有较大的方差。

假设我们有若干个样本点，并且我们想要将它们投影到一条过原点的直线上（假设数据已经进行了中心化处理）。这里，直线可以看作是一个方向向量u，并且u是一个单位向量。投影的过程实际上是将每个样本点x与方向向量u进行点积运算，得到的结果就是该样本点在u方向上的投影长度，即<x, u>（也表示为xT * u或uT * x）。

现在，如果我们选择两条不同的直线（即两个不同的方向向量u1和u2）进行投影，我们想要确定哪一条直线更好。根据方差最大化理论，我们应该选择使得投影后样本点之间方差最大的直线。在图中，左边的投影明显比右边的投影具有更大的方差（即投影点更分散），因此左边的投影是更好的选择。这是因为较大的方差意味着投影后的数据保留了更多的原始信号信息，而较小的方差则可能意味着更多的噪声被包含在内。

综上所述，当我们将n维样本点转换为k维特征时，我们希望找到一组方向向量（即k个主成分），使得样本点在这些方向上的投影具有尽可能大的方差，从而最大限度地保留原始信号的信息并减少噪声的影响。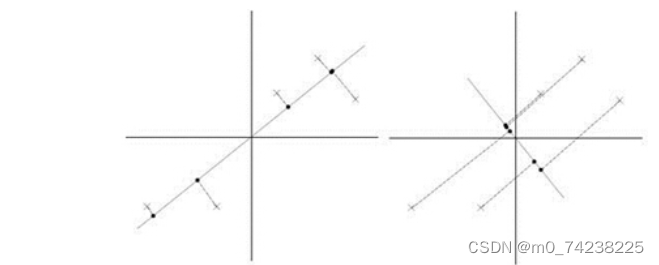


 

2. 最小二乘法
要证明特征向量的方向就是PCA中主成分的方向，我们需要从PCA的目标函数出发，并展示它如何与特征值和特征向量相关联。

首先，PCA的目标是最小化投影误差的平方和，这等价于最大化投影后的数据方差。假设我们有一个中心化后的数据集X，其形状为(n, d)，其中n是样本数量，d是特征数量。

PCA寻找一个单位向量u（即||u|| = 1），使得数据在u方向上的投影的方差最大。投影的方差可以表示为：

 Var(X⋅u)=1n∑ni=1(Xi⋅u)2=1n||Xu||2
 

由于u是单位向量，最大化投影方差等价于最大化||Xu||2
 

现在，我们考虑协方差矩阵Σ = X^T X / n。PCA的目标可以重写为最大化u^T Σ u，因为||Xu||^2 = u^T X^T X u = n u^T Σ u。

这是一个关于u的二次型，并且由于Σ是对称矩阵，它可以通过特征值分解表示为：

其中U是特征向量组成的正交矩阵，Λ是对角矩阵，对角线上的元素是Σ的特征值。

现在，考虑u^T Σ u：

由于u是单位向量，U^T u也是单位向量（因为U是正交矩阵）。设v = U^T u，则v^T v = 1。

现在，u^T Σ u可以表示为v^T Λ v，其中v是一个单位向量。由于Λ是对角矩阵，其对角线上的元素是特征值，因此v^T Λ v实际上是v中每个元素与对应特征值的乘积之和。由于v是单位向量，其元素平方和等于1，因此v^T Λ v的最大值出现在v与最大特征值对应的特征向量对齐时，即v是最大特征值对应的特征向量。

由于u = Uv，我们可以得出u是最大特征值对应的特征向量。因此，特征向量的方向就是第一主成分u1的方向。类似地，第二大特征值对应的特征向量的方向就是第二主成分的方向，以此类推。

注意：以上推导假设了数据已经中心化，即均值为0。如果数据没有中心化，需要先进行中心化操作。此外，PCA通常还涉及对特征向量进行排序和选择，以保留最重要的主成分。

用途与意义
PCA（主成分分析）是一种广泛使用的数据降维方法，它能够将原始的高维数据集转化为低维的表示，同时尽量保持原始数据的重要结构和特征。PCA降维的意义和用途主要体现在以下几个方面：

1. 数据压缩
PCA通过提取数据中的主要变化方向（即主成分），能够去除数据中的冗余和噪声，实现数据的有效压缩。在数据存储和传输方面，PCA能够显著减少所需的空间和时间，提高处理效率。
2. 可视化
对于高维数据，人类很难直接进行可视化和理解。通过PCA降维，可以将高维数据投影到二维或三维空间，使得数据点的分布和模式能够更直观地展示。这有助于我们更好地理解数据的内在结构和规律。
3. 特征提取
PCA能够提取出数据中的关键特征，这些特征通常能够代表数据的本质信息。在机器学习和数据挖掘中，这些特征可以作为输入特征用于训练模型，从而提高模型的预测性能和泛化能力。
4. 去除相关性
PCA通过正交变换，能够消除原始数据中的相关性。在回归分析、聚类分析等任务中，去除相关性能够简化模型，提高模型的稳定性和准确性。
5. 异常检测
由于PCA能够捕获数据的主体变化，因此可以识别出那些远离主体分布的异常点。这些异常点可能代表着特殊的数据或噪声，对于进一步的数据分析和处理具有重要的指导意义。
6. 预处理步骤
PCA常常作为其他机器学习算法的预处理步骤。例如，在分类或聚类任务中，PCA可以用于降低输入数据的维度，减少计算成本，并可能提高分类或聚类的效果。
7. 加速计算
对于高维数据，许多机器学习算法的计算复杂度会随着维度的增加而显著增加。通过PCA降维，可以显著减少这些算法的计算成本，加速模型的训练和推理过程。

实例及代码展示
以对人脸进行降维为例子：

1. 导入所需的库和模块

import os  
from PIL import Image  
import numpy as np  
from sklearn.decomposition import PCA  
import matplotlib.pyplot as plt

import os  
from PIL import Image  
import numpy as np  
from sklearn.decomposition import PCA  
import matplotlib.pyplot as plt

2. 设置图像目录并加载图像
 

image_dir = 'E:\\图片\\Camera Roll\\新建文件夹\\'  # 替换为您的图像目录  
images = []  
for filename in os.listdir(image_dir):  
    if filename.endswith('.jpg'):  # 假设你的图像是jpg格式的    
        img_path = os.path.join(image_dir, filename)  
        img = Image.open(img_path).convert('L').resize((32, 32))  # 转换为灰度并调整大小    
        images.append(np.array(img).flatten())  
  
X = np.array(images)

image_dir: 设置图像的目录路径。
images: 初始化一个空列表，用于存储图像的扁平化数组。
循环遍历目录中的每个文件，如果文件是.jpg格式，则加载它、转换为灰度图像、调整大小为32x32，然后将其扁平化并添加到images列表中。
X: 将images列表转换为NumPy数组，方便后续操作。

3. 选择要重建的图像

image_index = 0
这里选择索引为0的图像进行重建，即目录中的第一个图像。

4. 应用PCA并转换图像
 

pca = PCA(n_components=4, svd_solver='randomized', whiten=True)  
X_transformed = pca.fit_transform(X)

初始化一个PCA对象，设置主成分数量为4，使用randomized的SVD求解器（适用于大数据集），并设置whiten=True进行白化（使得每个特征的方差为1）。
使用fit_transform方法拟合PCA模型，并将所有图像样本转换到新的主成分空间。

5. 重建选定的图像

reconstructed_image = pca.inverse_transform(X_transformed[image_index:image_index + 1]).reshape(32, 32)
使用PCA的inverse_transform方法将选定的主成分表示转换回原始图像空间。
因为inverse_transform的输入是一个二维数组，所以我们使用切片X_transformed[image_index:image_index + 1]来获取单个图像的表示。
使用reshape(32, 32)将扁平化的数组重新整形为32x32的图像。

6. 绘制重建的图像
 

plt.imshow(reconstructed_image, cmap='gray')  
plt.title('Reconstructed Image with 4 Components')  
plt.axis('off')  
plt.show()

使用matplotlib.pyplot的imshow方法绘制重建的图像。
设置颜色映射为灰度（cmap='gray'）。
添加标题说明这是使用4个主成分重建的图像。
关闭坐标轴（axis('off'）。
显示图像。
原图与降维后的图：

 

分析总结
这段代码的主要目的是从给定目录加载一系列JPEG图像，将它们转换为灰度并调整大小，然后使用PCA进行降维，并重建其中一个图像以查看降维的效果。通过选择4个主成分，代码展示了如何使用PCA在保持图像大部分信息的同时减少数据的维度。

优缺点分析
优点：
数据降维：PCA能够通过识别数据中的主成分来降低数据的维度，这使得数据更容易理解和可视化，同时也减少了计算复杂性和存储空间需求。
特征提取：PCA提取的主成分通常反映了数据中的最重要信息，这些成分可以被视为原始数据的特征，用于后续的机器学习或统计分析。
减少噪声和冗余：由于PCA只保留数据中的主成分，因此可以消除一些噪声和冗余信息，从而提高数据的信噪比。
无参数限制：PCA是一种无参数方法，它不需要用户指定要保留的成分数量，而是通过方差解释比例等标准自动确定。
易于实现：PCA的实现相对简单，并且有很多现成的库和工具可以使用，例如scikit-learn等。

缺点：
对异常值敏感：PCA对数据的异常值非常敏感，因为它们会显著影响数据的均值和协方差矩阵，从而影响主成分的计算。
解释性不强：PCA提取的主成分通常是原始特征的线性组合，这些组合可能难以解释其实际意义，尤其是当原始特征数量较多或相关性较高时。
非线性关系无法捕捉：PCA只能捕捉数据中的线性关系，如果数据中存在非线性关系，PCA可能无法有效地提取这些关系。
信息损失：PCA在降维过程中会丢失一些原始信息，因为它只保留了数据中的主成分。如果保留的成分数量过少，可能会导致信息损失过多，影响后续分析的效果。
对参数敏感：虽然PCA本身不需要用户指定参数，但在实际应用中，用户通常需要决定保留多少主成分。这个决定对PCA的效果有很大影响，但很难确定一个最优的数值。
不适用于高维小样本数据：当样本数量小于特征数量时，PCA的效果可能不理想，因为协方差矩阵可能不是满秩的，导致无法计算主成分。