二叉树的定义
二叉树是另一种树形结构,其特点是每个节点至多只并且二叉树的子树有左右之分,其次序不能任意颠倒。有两棵子树(即二叉树中不存在度大于2的节点),与树相似,二叉树也以递归的形式定义。二叉树是n (n≥0)个节点的有限集合:
要么为空二叉树,即n=0;要么由一个根节点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
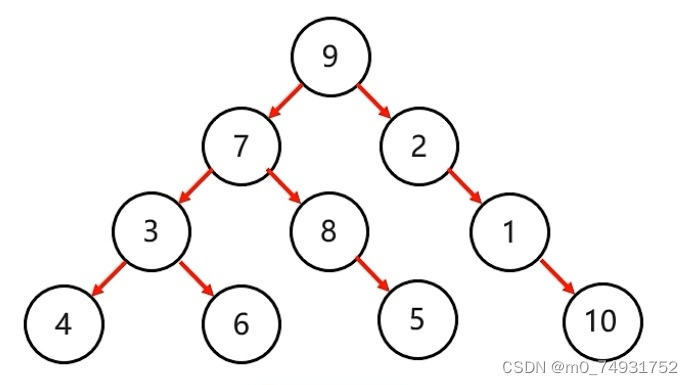
二叉树是有序树,若将其左、右子树颠倒,则成为另一棵不同的二叉树。即使树中节点只有一棵子树,也要区分它是左子树还是右子树。以下是普通二叉树示例图:
二叉查找树的定义
二叉查找树(Binary Search Tree,又称二叉排序树或二叉搜索树)是一种特殊的二叉树数据结构,具有以下定义:
节点键值特性: 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值。
若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值。它的左、右子树也分别为二叉查找树。
递归结构:二叉查找树是一种递归数据结构,即每个非空子树也都是一个二叉查找树。
等价定义:若以中序遍历二叉查找树,则会产生一个所有节点关键字值的递增序列。
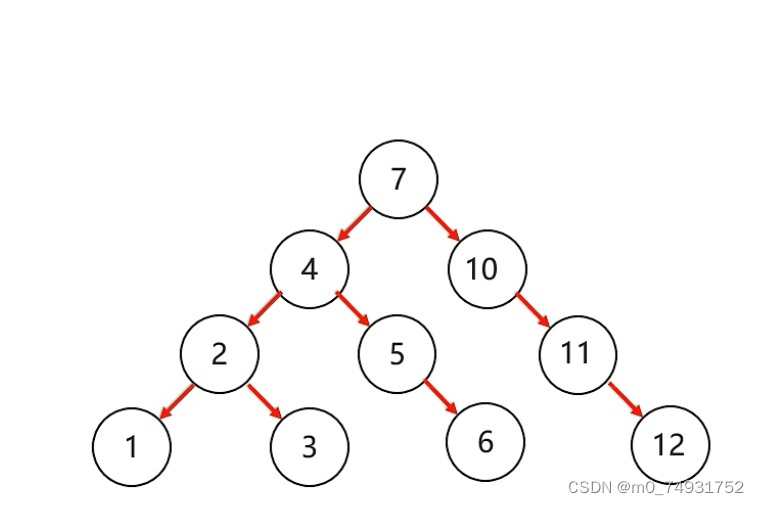
二叉查找树的优势在于它的有序性,这使得在二叉查找树上进行搜索、插入、删除等操作的时间复杂度与树的高度成正比。对于一棵含有n个结点的完全二叉树,这些操作的时间复杂度O(log2n)。但是,如果树是含有n个结点的线性链,则这些操作的最坏情况下的运行时间为O(n)。以下是二叉查找树示例图:
前序、中序、后序、层序遍历讲解
1前序遍历(Preorder Traversal):
遍历顺序:首先访问根节点,然后遍历左子树,最后遍历右子树。
特性:根节点在左右子树之前被访问。
示例:对于二叉树A(B(D,E),C(F,G)),前序遍历结果是A B D E C F G。
2中序遍历(Inorder Traversal):
遍历顺序:首先遍历左子树,然后访问根节点,最后遍历右子树。
特性:根节点在左右子树之间被访问,常用于二叉查找树的排序操作。
示例:对于二叉树A(B(D,E),C(F,G)),中序遍历结果是D B E A F C G。
3后序遍历(Postorder Traversal):
遍历顺序:首先遍历左子树,然后遍历右子树,最后访问根节点。
特性:根节点在左右子树之后被访问。
示例:对于二叉树A(B(D,E),C(F,G)),后序遍历结果是D E B F G C A。
4层序遍历(Level-order Traversal):
遍历顺序:按照树的层级从上到下、从左到右进行遍历。
特性:逐层访问节点,常用于完全二叉树或需要层次信息的场景。
示例:对于二叉树A(B(D,),C(E,F)),层序遍历结果是A B C D E F(注意:这里假设B的右子树为空,且C的左子树为E,右子树为F,以符合层序遍历的常规展示)。
 平衡二叉树
平衡二叉树
定义:平衡二叉树(Balanced Binary Tree),又称AVL树,是一种特殊的二叉排序树。它要求树中任意节点的左子树和右子树的高度之差的绝对值不超过1,并且左右两个子树都是平衡二叉树。
性质:高度平衡:通过保持树的平衡,确保树的高度尽可能低,从而提高搜索、插入和删除操作的效率。
二叉排序树特性:满足二叉排序树的所有性质,即左子树上所有节点的值都小于根节点的值,右子树上所有节点的值都大于根节点的值。
平衡因子:为了衡量一个节点的平衡状态,引入了平衡因子(Balance Factor)的概念。平衡因子定义为该节点左子树的高度减去右子树的高度。在平衡二叉树中,所有节点的平衡因子只能是-1、0或1。
调整机制:当对平衡二叉树进行插入或删除操作后,可能会导致树的不平衡。为了恢复平衡,需要进行旋转操作,包括单旋转(左左旋转、右右旋转)和双旋转(左右旋转、右左旋转)。
如图示展现: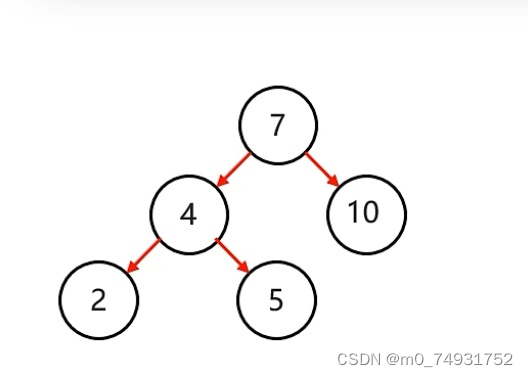
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








