理解int转float为何会可能精度丢失的问题

         在看Java核心技术卷I的时候，看到个基础类型转换，图片就不附上了，上面写到int转float有可能会精度丢失，看到此处的时候我一直在疑惑，明明float能够表示的数比int要大得多，怎么可能int转到float的时候会精度丢失呢？？？原谅我是个小菜鸟。

         第二天回到公司与同事几乎研究了一早上，最后发现主要实际上是int和float的存储结构是不同的。

         曾在百度上搜到一个很形象的答复，就是int是准确值，而float是精确值，准确转精确当然会精度丢失。

         Int是4字节32位来表示的，而float虽然也是4字节32位，但是float的存储结构是很不一样的

   

 

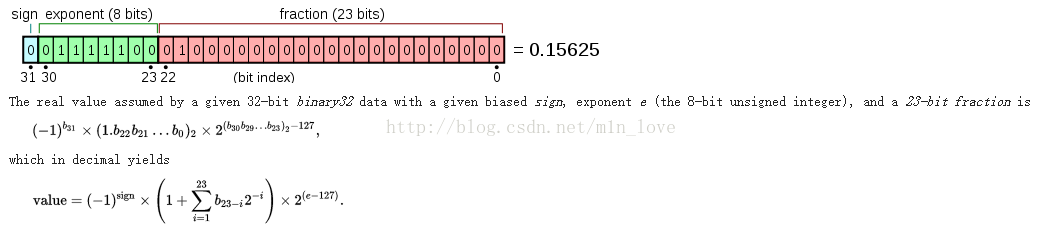
         以这一例子来说明，由图可知，float的存储结构是1个符号位，8个指数位，23个尾数。

 

符号位，表述浮点数的正或者负，0代表正，1代表负。

 

指数位，实际也是有正负的，但是没有单独的符号位，在计算机的世界里，进位都是二进制的，指数表示的也是2的N次幂，8位指数表达的范围是0到255，而对应的实际的指数是－127到128。也就是说实际的指数等于指数位表示的数值减127。这里特殊说明，－127和＋128这两个指数数值在IEEE当中是保留的用作多种用途的，这里就不多做介绍了，有兴趣的可以查阅其他资料。

 

尾数位，只代表了二进制的小数点后的部分，小数点前的那位被省略了，当指数位全部为0时省略的是0否则省略的是1。

 

由此我们可以明白，实际上尾数确定了浮点数的精度，而数的大小主要是靠指数位，尾数只有23位，加上省略的那一位便是24位，所以如果int类型的值在2^24以内，float是可以精确表示的，但是当超过这个数的时候就不一定能精确表示了。这里最重要的一点便是要理解确定精度的有效位数，不管是什么基本类型转换实际上都要明白这一点。就如我此博文讲的int与float，都是32位，但是内存结构既存储结构是不一样的，float只能有24位来确定精度，而int是32位。其他类型也如此进行理解即可。

 

接下来讲解一下上面的公式理解：：：

在讲这公式之前讲一下我在理解过程中遇到的难题，就是尾数的23位值为什么是介于1.0和2.0之间，当时看到一直想不明白，后来才了解到这23位是用来表示小数位的，而省略的那一位是1，因为0是没有意义的（因为如果是0，一个小数的不管乘以多少都是小数）。再次强调这里的尾数23位是表示小数位的。

 

再次贴一下图片。。

就以图的例子来讲。

符号位我想不用我讲了

指数位就跟我们算十进制一样的方法，可以算出指数位是124（算法我就不在这里说了，网上自己查一下），套入以上的表达式的最后一个，既是2^(124-127) = 2^(-3)

然后尾数部分，看它的公式就可以看出来，b23-i就是尾数部分的哪一位数，i取1的时候就b22，既最左边的部分，然后再乘以2的负i次方。从上面这一公式也可以看出，尾数部分是介于1.0和2.0之间。

 

最后3个部分相乘就得出正确的结果了。

 

 

PS：第一次写博客，可能写的不太好，希望大家见谅，上面的内容部分是转载的，也有可能有地方出错了，欢迎大家指出，谢谢。