M2M寻径算法

基于粒计算思想的M2M寻径算法

摘要

宏观微观（M2M）模型是一种源于粒计算思想并扩展了许多有价值的特性的算法设计模型。本文我们介绍了一个基于M2M模型的分层寻径算法。该算法花费O(n)时间预处理建成M2M数据结构，这样的层次结构占有O(n)位存储空间并且可在O(1)估计时间内被更新处理各种变化。虽然找到的路径不总是最短的路径，但是它可以通过一个调整一个参数—范围值在精确度与时间开销之间作权衡，以满足各种应用。最后，我们将讨论M2M寻径算法的优点和说明M2M模型的学术和应用前景。

1. 引言

寻径对很多领域来说是至关重要的，例如多智能体系统，即时战略游戏，因特网路由系统，汽车导航系统。现代硬件增加的处理能力和内存帮助寻径迈出了一大步。然而，下一代环境增加的复杂性造成我们飞跃倒退。动态障碍，变化的环境，3D场景和大规模智能体的导航任务使到运算能力后退了几代。

在大地图上的寻径任务，特别是在三维地图上，对寻径算法的效率有很高的要求。此外，不断变化的局部地图, 包括弧线和顶点的变化，需要寻径算法具有更好的动态性。

本文我们介绍了一个基于M2M模型的分层寻径算法。该算法花费O(n)时间预处理建成占有O(n)位存储空间的M2M数据结构，然后它能够快速查询图中两个节点的路径。这种数据结构有一个理想的特性那就是能在O(1)估计时间内被更新来处理原始图的一个弧线或顶点的变化。虽然找到的路径不总是最短的路径，但其解决方案的质量非常接近于最优。而且, 它可以通过一个调整一个参数—范围值在精确度与时间开销之间作权衡，以满足各种应用。

粒计算的基本思想在很多领域被探究，例如人工智能，区间分析（interval analysis），量化（quantization ），粗糙集理论（rough set theory），分而治之（divide and conquer），聚类分析（cluster analysis），机器学习等[1]， M2M模型是一个具体的模型，它提供了关于如何设计和实现粒计算思想如多视角和逐步细化（multiple views and step-wise refinement）的指引和法则。

另外，M2M模型延伸了粒计算思想并强调许多额外的非常有价值的特性。这些特性与人类的行为相一致，但很少在其它计算模型中被提到。 这些有价值的特性是共享预处理、鲁棒性与容错性、动态性等。

M2M模型生成的数据结构被有效地用于解决基于点集（point-set-based）的问题，如最近邻查询问题[4]和凸包问题[5]等。

2.相关工作

Dijkstra是最经典的单源最短路径算法，但它在缩小搜索空间方面是有弱点的。后来，A* [6]因为其启发式方法变成使用最广泛的寻径算法。IDA* [7] 是一种A*的改进。，A* 和IDA*在静态环境中已彻底探讨关于寻找最佳路径。（have been explored thoroughly with regard to finding optimal paths in a well-known and stationary environment. ）如果环境改变，D*-Lite [8]可以做有限的重新规划，但它不能处理运动目标所造成的的变化。

近年来，对地图建立抽象和分层对寻径问题无疑是一个有效的办法。Holte [9]在问题空间的图示中用抽象和逐步细化的方法来减少时间开销。 抽象和逐步细化能够被用于为非抽象空间[10]建立启发式功能（heuristic functions）。代替从图示中直接抽象，(HPA*) [2]用大sectors 覆盖地图并且计算入口与出口到sectors的有限集的最优路径。虽然过程平滑，但最优路径可以得到。 (PRA*) [3] 使用自动状态空间抽象以改进传统的寻径算法。 它采用图抽象的层次并且用该层次计算抽象的路径。

基于这样的假设，某一道路网络没有经常的变更。许多文献介绍使用相当大的内存和时间开销来预处理一些节点之间的最短路径的方法以提高后来寻径的速度。大多数这些算法保证了准确的最短路径，但是他们动态性很差，因为任何弧线或顶点的变化都将可能引起预处理最短路径无效。

3.术语解释

层: 图G=(V,E) 的分层数据结构包括不同粒度的各层。一个粗粒度的层代表在宏观视图的抽象的数据分类。一个细粒度的层代表在微观视图的详细的数据分类。

分块: 分块被定义为跟粒计算中颗粒（grain）概念相似的数据点的子集。在第k层，图G=(V,E) 被分为同样尺寸的正方形区域。小正方形中的所有数据点都属于该分块。

4.M2M数据结构范式

 

     

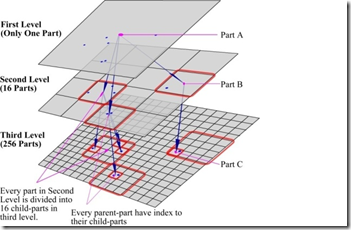
图1显示的是M2M数据结构的一个例子。M2M模型的具体实现视乎不同的情况而不同。但有一些基本的条件必需满足粒计算思想和M2M模型的要求。

1. 已知数据点，用O（1）的时间能检索出该点在指定的层所属的分块。这个属性确保数据结构可以容易地改变粒度容易。(粒计算条件)

2. 能够用O（1）的时间来把该数据点插入到在M2M数据结构中插入或删除一个数据点。这个属性确保它是一个动态的结构。（M2M条件）

3. 已知某分块的索引，用O（n）的时间能遍历该分块的所有子分块，n为该分块的子分块数。这个属性确保可用性和逐步细化过程的速度。（粒计算条件）

4. 预处理时间复杂度为O（n）。同时支持并行处理。 (M2M条件)

5.寻径的M2M数据结构

M2M寻径的数据结构是基于一般的M2M数据结构的，并且它增加了不同粒度的所有层中分块的连通信息。因此我们可以遵循粗粒度层的连通关系处理细粒度层。

6.M2M寻径算法

正如其它M2M算法的一般过程，M2M寻径算法主要包括两个步骤：预处理与查询。预处理仅运行一次来创建用于路径搜索的M2M数据结构。如果之后地图发生细微变更，可以对M2M数据结构进行更新操作。预处理之后，一旦搜索任务被确定，查询的程序就可以在很短的时间内被执行。

7.M2M寻径的预处理过程

预处理分析每个分块的连接部分（components）并从细粒度层次到粗粒度层次构造一个分层的数据结构。

在第k层，图G=(V,E)被分为面积相同的正方形分块：Part₁(k), Part₂(k), …, Part_n(k). 每一个分块对应于下一个子图 并且 。之后每个