目录
前言
在数据结构的知识体系里,二叉树是承载递归思维与分层遍历的核心结构,而堆作为完全二叉树的典型应用,更是将 “优先级筛选” 的能力发挥到了极致。在面试与工程实战中,TopK 问题(找前 K 大、前 K 高频元素等)一直是高频考点,暴力排序的思路往往因时间复杂度过高被淘汰,而堆结构正是解决这类问题的最优解之一。本文将从二叉树的底层逻辑出发,拆解堆的构建与调整过程,再结合经典 TopK 例题,带你吃透从原理到代码的完整链路。
(本文中log都是以2为底的log,如果标注了的没事,看到logn,希望大家可以知道什么意思)
树
我们先看一下官方的说法什么是树
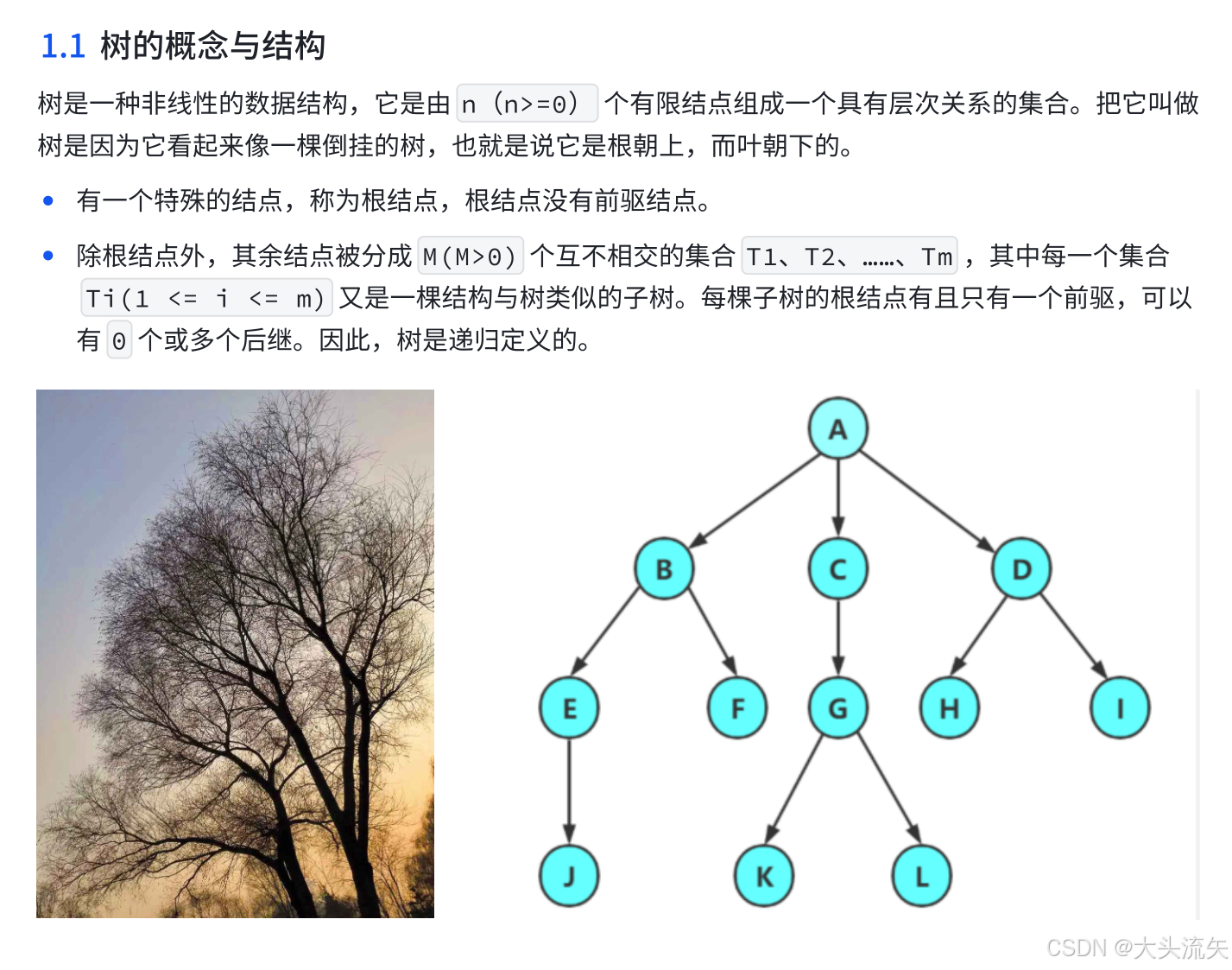
看不懂没事我来给大家用通俗的话说一遍
假设
A为爷爷辈
B、C、D为爸爸辈
E、F、G、H、I为我这辈
J、K、L为我孩子这辈
-------------------------------------------------------------------------------------------------------------------------
那么树的概念就是
- 爷爷辈的结点可以链接爸爸辈的结点,爸爸辈结点可以链接我这辈的结点。
- 爷爷辈结点、爸爸辈结点又可以通过我找到我孩子这辈结点,但是爷爷辈结点和爸爸辈结点不能直接越过中间结点直接连接我的孩子结点
- 上一辈的可以连接多个下一辈的结点,
- 下一辈的结点只能有一个上一辈的结点连接,
- 同辈的结点不能互连,
- 而且上一辈的结点不能连接同一个下一辈结点
(就和我们的血缘关系一样,我们的直系亲属只能是我们的父母,总不能大伯也是我们的直属亲戚叭,他只是爸爸的兄弟,但是和我们没有直接关系,只是通过爸爸产生了间接关系,因为他和爸爸是兄弟)
非树
先看非树的结构
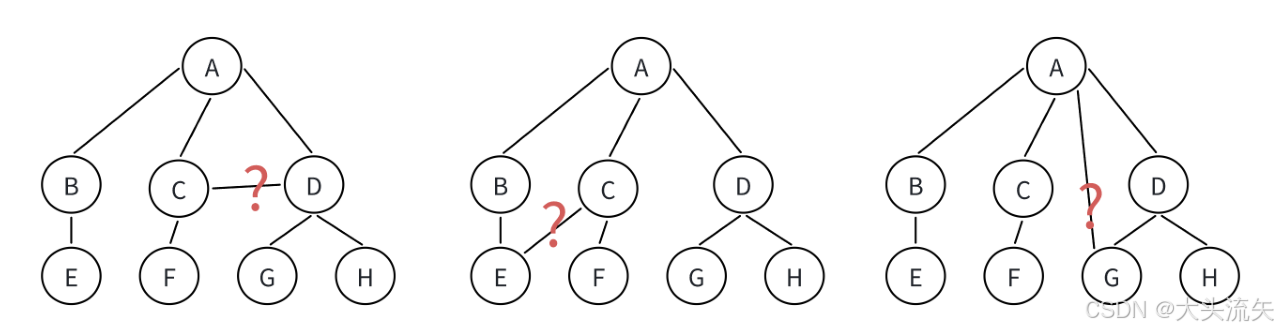
大家可以对照我刚刚上面说的树的结构来对比一下,为什么他是非树结构
- 同辈结点相连
- 同辈结点连接到同一个下一辈结点
- 上一辈的结点只能连接到下一辈的结点,不能直接略过下一辈的节点,直接连接
树的相关术语
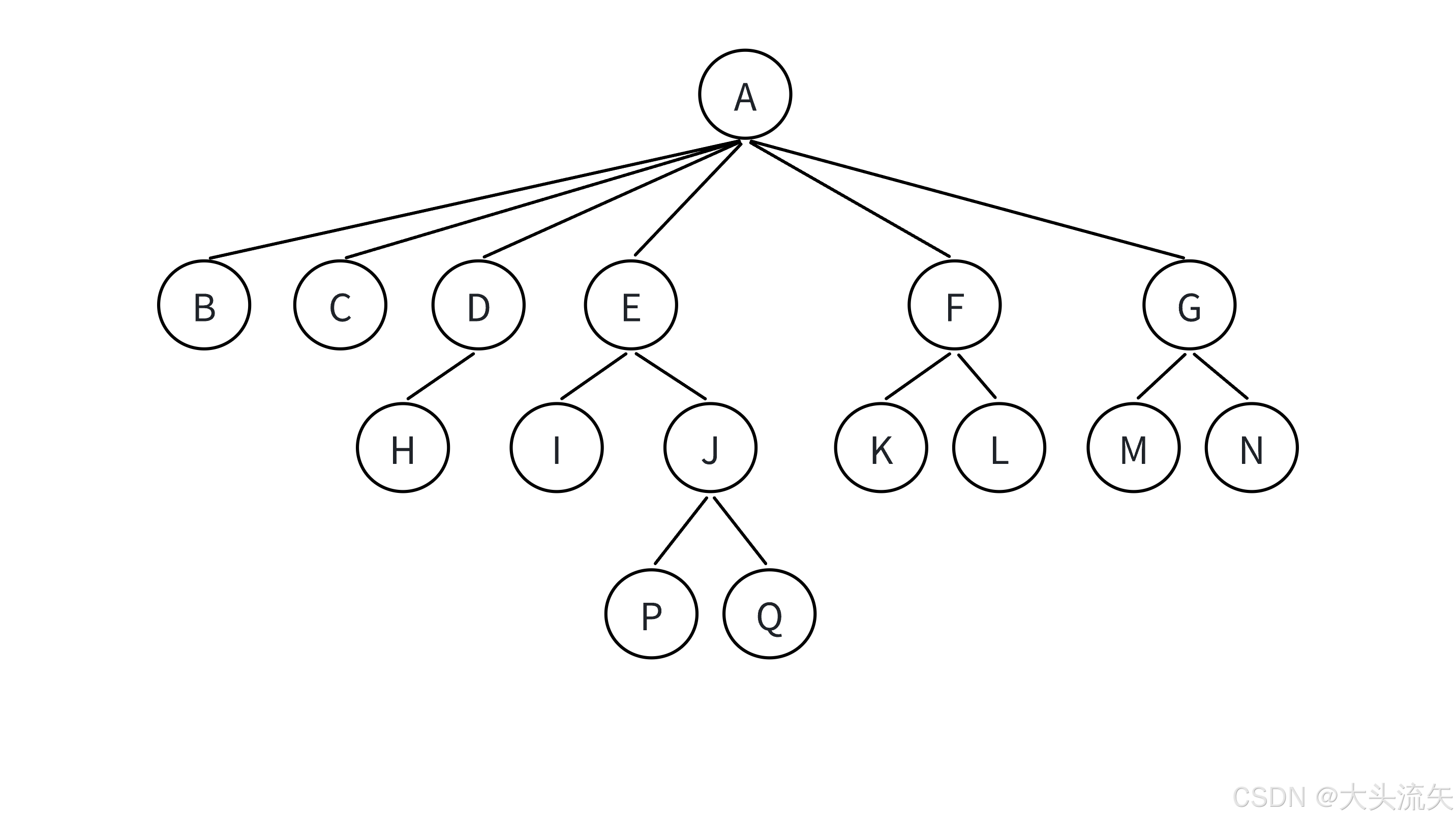
| 概念名称 | 定义 | 示例(对应题干中的树) |
|---|---|---|
| 父结点 / 双亲结点 | 若一个结点含有子结点,则这个结点称为其子结点的父结点。 | A 是 B 的父结点,E 是 J 的父结点,J 是 Q 的父结点。 |
| 子结点 / 孩子结点 | 一个结点含有的子树的根结点称为该结点的子结点。 | B 是 A 的孩子结点,J 是 E 的孩子结点,Q 是 J 的孩子结点。 |
| 结点的度 | 一个结点拥有的子结点的数量(即有几个孩子,度就是多少)。 | A 的度为 6,F 的度为 2,K 的度为 0,E 的度为 1,D 的度为 1。 |
| 树的度 | 一棵树上所有结点中,最大的结点度数即为树的度。 | 树的度为 6(因 A 结点的度最大,为 6)。 |
| 叶子结点 / 终端结点 | 度为 0 的结点(没有任何子结点的结点)。 | B、C、H、I、K、L、M、N、O、P、Q 等结点(均无子女)。 |
| 分支结点 / 非终端结点 | 度不为 0 的结点(至少有一个子结点的结点)。 | A、D、E、F、G、J 等结点(均有子女)。 |
| 兄弟结点 | 具有相同父结点的结点互称为兄弟结点(亲兄弟)。 | B 和 C 是兄弟结点(父结点均为 A);K 和 L 是兄弟结点(父结点均为 F)。 |
| 结点的层次 | 从根结点开始定义,根为第 1 层,根的子结点为第 2 层,依次递增。 | A 是第 1 层;B、C、D、E、F、G 是第 2 层;H、J、K、L、M、N 是第 3 层;Q 是第 4 层。 |
| 树的高度 / 深度 | 树中所有结点的最大层次(即最深结点的层次)。 | 树的高度为 4(最深结点 Q 处于第 4 层)。 |
| 结点的祖先 | 从根结点到该结点所经过分支上的所有结点(包括根和父结点)。 | A 是所有结点的祖先;A、E、J 是 Q 的祖先;A、D 是 H 的祖先。 |
| 路径 | 从树中任意一个结点出发,沿 “父结点→子结点” 的连接,到达另一个任意结点的序列(路径上的结点不重复)。 | A 到 Q 的路径:A→E→J→Q;H 到 Q 的路径:H→D→A→E→J→Q;F 到 L 的路径:F→L。 |
| 子孙 | 以某结点为根的子树中,所有的结点都称为该结点的子孙(包括直接子结点和间接子结点)。 | 所有结点都是 A 的子孙;J、Q 是 E 的子孙;K、L 是 F 的子孙。 |
| 森林 | 由 m(m>0)棵互不相交的树组成的集合(多棵独立的树放在一起即为森林)。 | 若将题干中的树拆分为 3 棵互不相交的小树(如:以 B 为根的树、以 C 为根的树、以 D 为根的树),这 3 棵树组成的集合就是森林。 |

- 原先我们说的:
- 上一辈结点就是父节点
- 同辈节点就是兄弟结点
- 下一辈结点就是子结点
二叉树
在树形结构中,我们最常⽤的就是⼆叉树,⼀棵⼆叉树是结点的⼀个有限集合,该集合由⼀个根结点
加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。
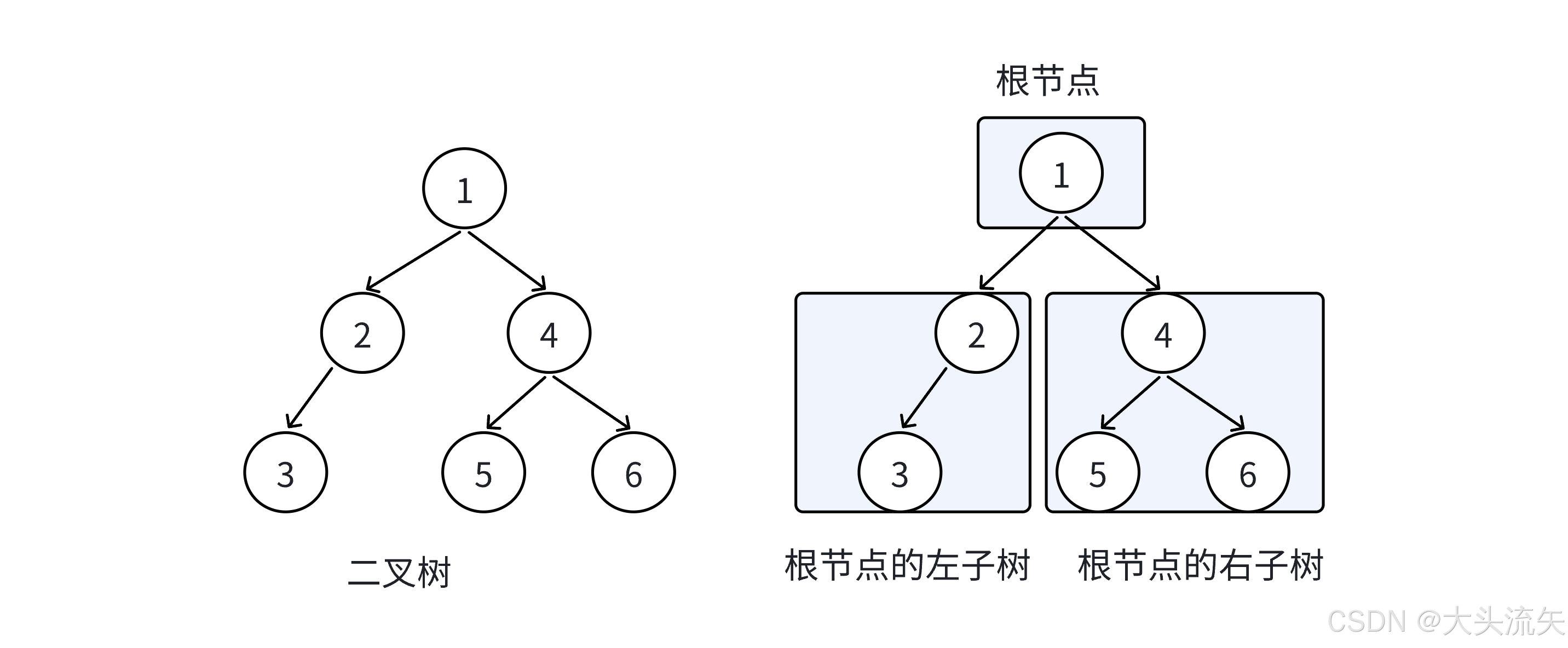
从上图可以看出⼆叉树具备以下特点:
1. ⼆叉树不存在度⼤于 2 的结点
2. ⼆叉树的⼦树有左右之分,次序不能颠倒,因此⼆叉树是有序树
注意:对于任意的⼆叉树都是由以下⼏种情况复合⽽成的
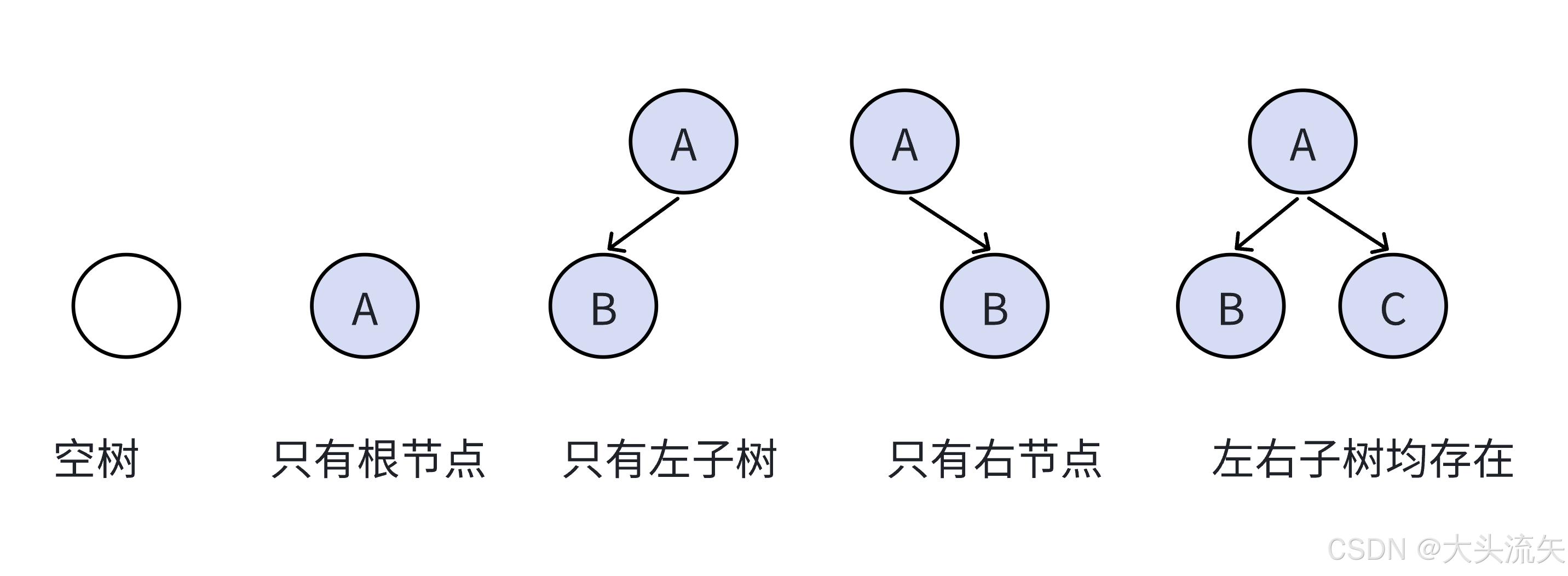
二叉树的分类
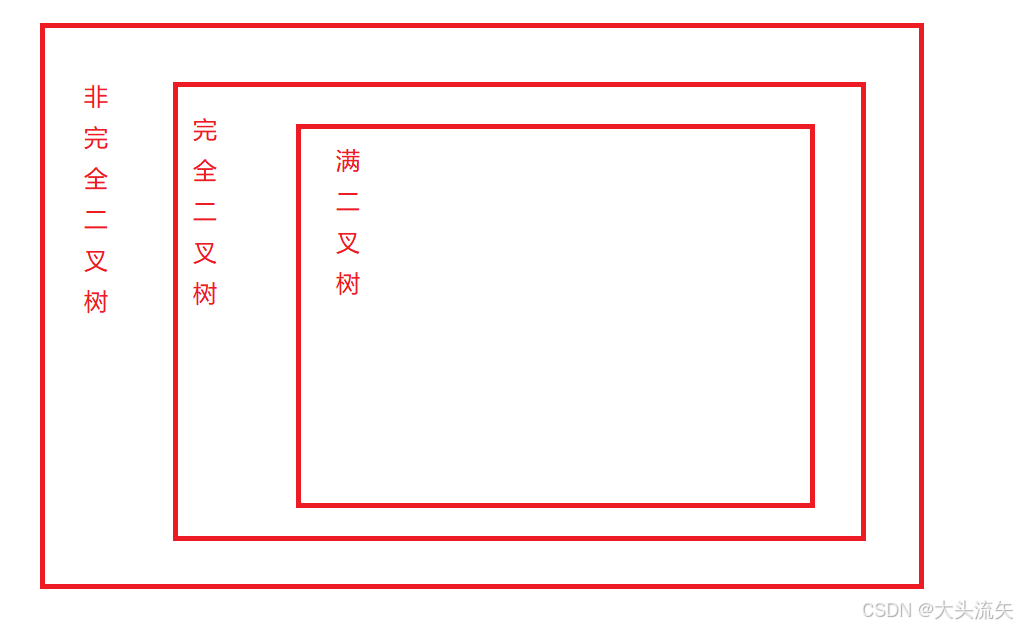
树有三种:非完全二叉树、完全二叉树、满二叉树
三者的关系:前者包含后者
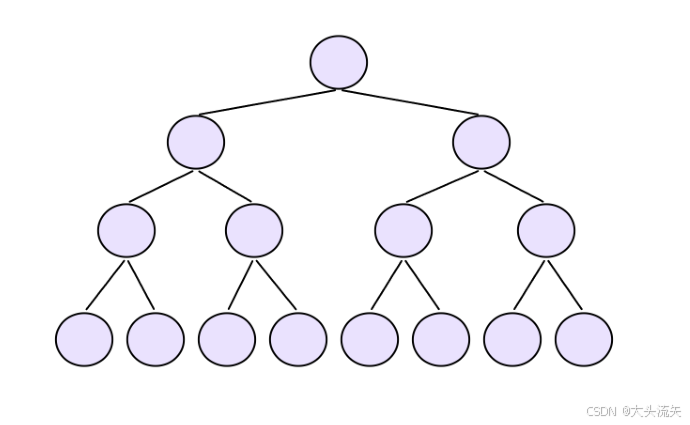
完全二叉树
所有的子结点都是连续的,这种结构也是我们二叉树经常用到的逻辑结构,因为这种结构用顺序表来存储空间的利用率高
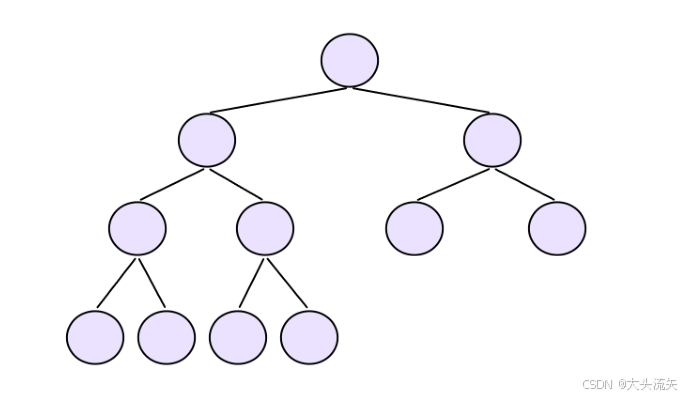
非完全二叉树
在子结点里你发现,第3层的结点里有一个没有子节点,但是他右边的兄弟结点却都有子结点,所以他是不连续的是非完全二叉树
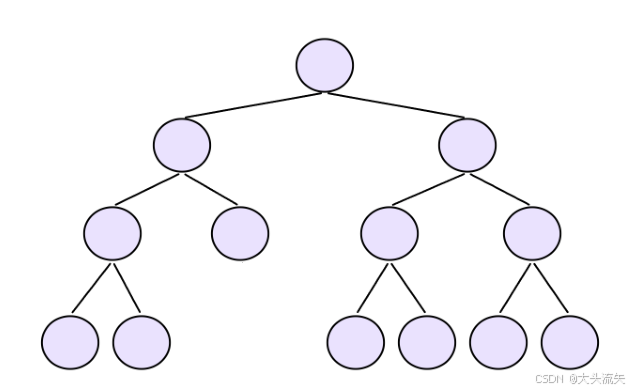
满二叉树
这种是二叉树的理想结构,除最后一层结点每一个父节点都有俩个孩子
计算完全二叉树和满二叉树的高度和结点数
满二叉树:
高度:h
总结点数:N
根据满二叉树的特点可以得出公式:
F(N) = 2^0 + 2^1 + 2^2 + 2^3 + ... + 2^(h-2) + 2^(h-1)
2F(N) = 2^1 +2^2 +2^3 + 2^4 + ... + 2^(h-2) + 2^h
2F(N)-F(N) =F(N)=2^h - 1
F(h) = log (N+1)----(log以2为底的(N+1))
(2)
高度公式:h = log (N+1)----(log以2为底的(N+1))
(2)
总结点公式:N = 2^h - 1
第h层的结点数:n = 2^(h - 1)
完全二叉树:
高度:h
总结点数:N
完全二叉树不同于满二叉树,它的最后一层结点不是满的,但是他的h-1层一定是满的,所以我们可以先利用满二叉树的公式取一个值范围
N的取值范围:2^(h-1) <= N <= 2^h - 1
我来解释这个公式,因为完全二叉树的h层必须最少有1个叶子结点
按照这个逻辑来说,那么前(h-1)层的总结点数是不就为2^(h-1) - 1个结点嘛,但是这是前(h-1)层的,第h层最少还有1个叶子结点,所以加起来不就等于2^(h-1)嘛
完全二叉树的最大情况就是满二叉树的情况,所以就是2^h - 1
h最小高度公式:log (N)<= h <=log (N+1)
(2) (2)
我们取:log (N+1)
(2)
二叉树的存储结构
二叉树我们一般分为2种存储结构:顺序表的连续存储、链表的链式存储
顺序结构
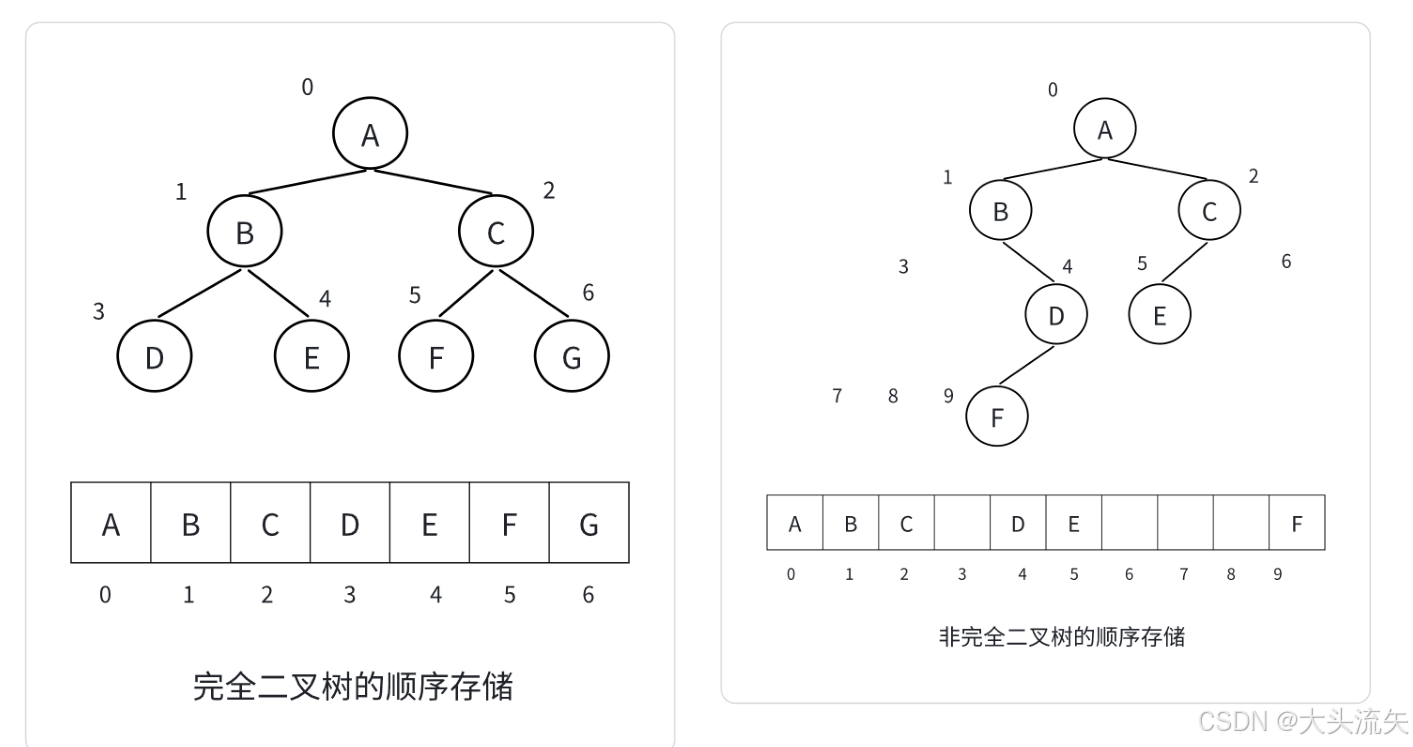
其实我们之前也讲了完全二叉树的逻辑结构上所有的子结点都是相邻的,而这种相邻的结构就非常适合用顺序表数组来存储,反观非完全二叉树,因为子结点存在不相邻的情况,所有在顺表数组中存储就会导致空间的浪费
当我们只是把左图的数据从逻辑结构的数,存储到物理结构的数组里的时候,那么恭喜你解锁了,在二叉树的逻辑结构和物理结构之间转换的能力
链式结构
二叉树的链式存储结构是通过链表来表示二叉树,利用指针来体现节点间的逻辑关系。
在具体实现中,每个链表节点包含三个部分:数据域存储节点值,左右指针域分别指向该节点的左孩子和右孩子的存储地址。根据指针数量不同,链式结构可分为二叉链(含左右两个指针)和三叉链,在今天我们主要使用二叉链结构。
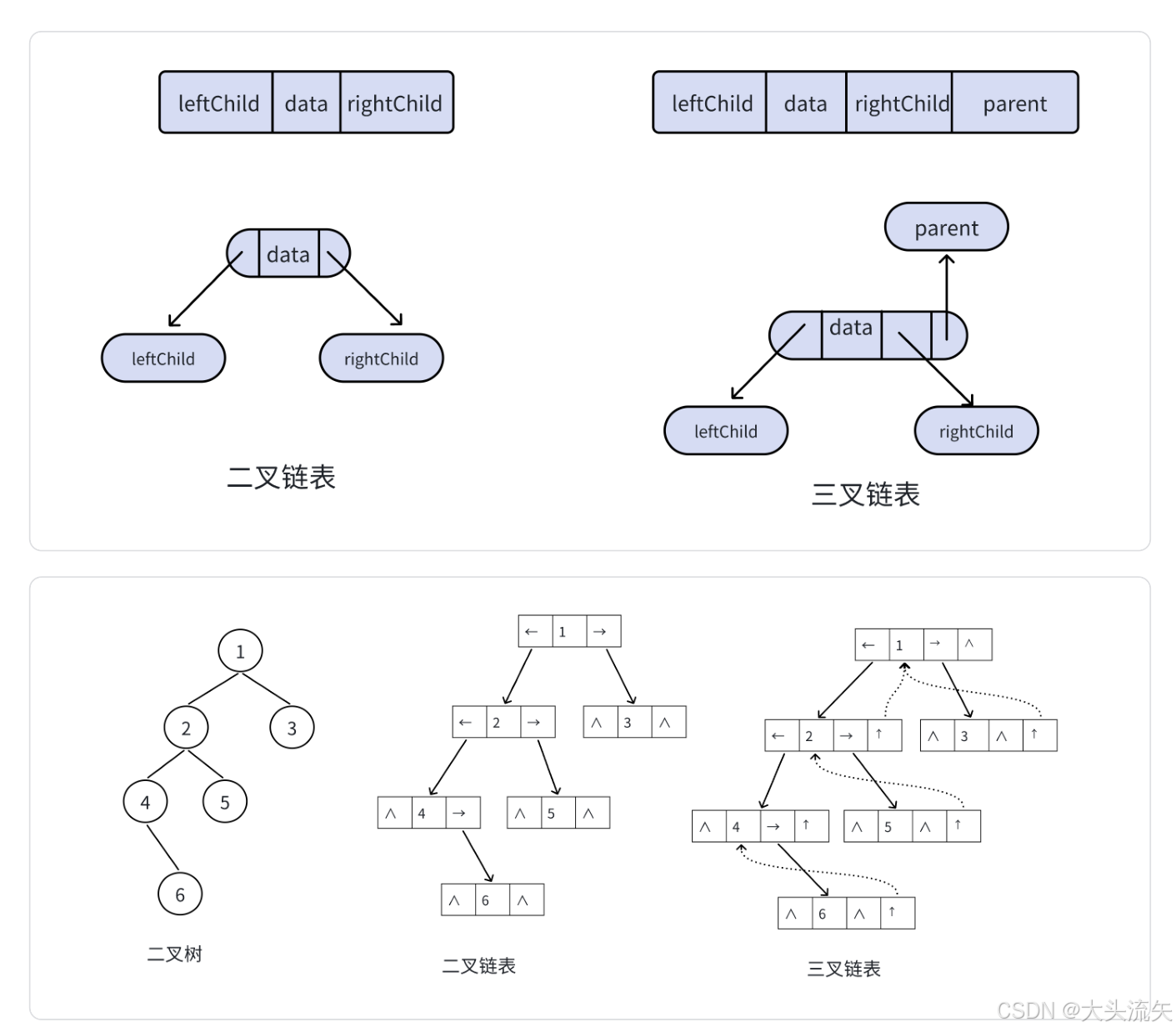
这种链式存储就非常的适合存储非完全二叉树,很好的解决了父节点左右子树为空的情况,更大程度上减少了空间的浪费
实现顺序结构二叉树
当我们的思维可以把完全二叉树的逻辑结构转化为物理结构的时候,那么我就可以想想怎么去实现这个顺序结构的二叉树了,实现顺序结构的二叉树必须要知道堆
堆的概念与结构
这个堆和内存里面的对可不一样,内存的堆是物理器件上的一部分,而我们说的这个堆是一种存储方式
堆分为:
- 大堆
- 小堆
大堆就是每个父结点都大于自己的子结点
小堆就是每个父结点都小于自己的子结点
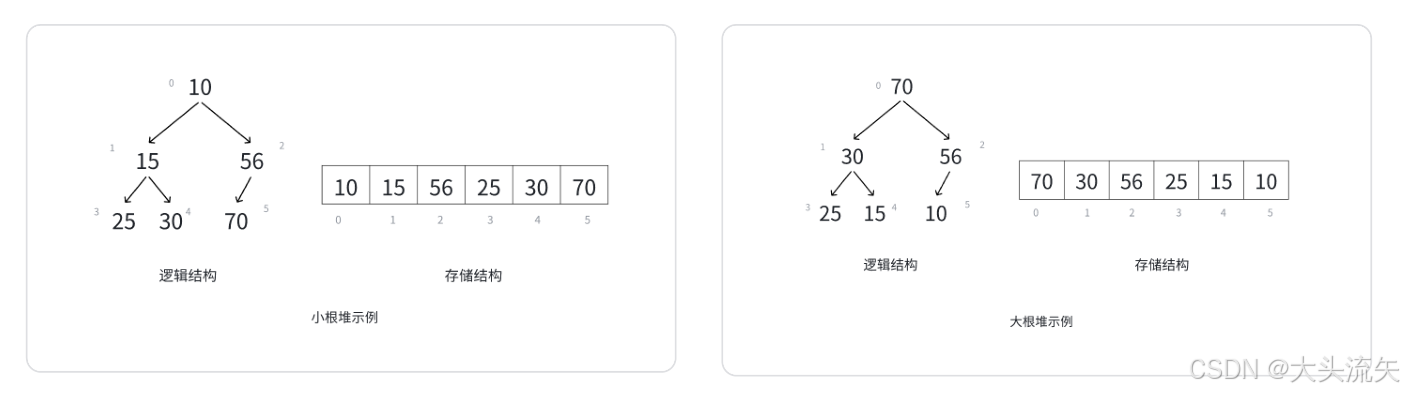
存储的方式大家也可以参考这俩张图里的,无论大堆还是小堆,都是从根结点开始存储
接下来再和大家说一下堆的性质

堆的实现
先看一下实现堆的整体代码板块
typedef int HPDataType;
typedef struct Heap
{
//堆的首元素地址
HPDataType* a;
//堆当前存储的元素个数
int size;
//堆可存储的最大个数
int capacity;
}HP;
//堆排序
void HeapSort(int* a, int n);
//交换
void Swap(HPDataType* a, HPDataType* b);
//堆的初始化
void HeapInit(Heap* php, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
//堆的向上调整
void HeapJustUp(HPDataType* a, int n);
//堆的向下调整
void HeapJustDown(HPDataType* a,int n);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
老样子我们还是在VS2022的环境下执行,分别创建三个文件Heap.h(函数声明)、heap.c(函数实现)、test.c(代码测试)
堆的初始化
//参数(Heap结构体的地址,一个数组地址,数组的元素个数)
void HeapInit(Heap* php, HPDataType* a,int n)
{
assert(php);
assert(a);
php->a = NULL;
php->capacity = 0;
php->size = 0;
//后续会用HeapPush函数直接在初始化这一步就把堆建好
for (int i = 0; i < n; i++)
{
HeapPush(php, a[i]);
}
}堆的值交换
//交换,后续会用到很多的的交换部分,所有就单独拿出来
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType swap = *a;
*a = *b;
*b = swap;
}获取堆顶元素、堆的数据个数、堆的判空、堆的销毁
因为这几个比较简单,所有我就拿出来放一起了
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
if (hp->size == 0)
{
return 0;
}
else
{
return hp->size;
}
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->capacity = 0;
hp->size = 0;
}*建堆
首先先介绍一下向上调整法和向下调整法
向上调整法
从后往前依次比较自己的父结点,看谁大谁小,符合条件就交换
使用前提:父结点及以上为堆(大堆小堆都可以)

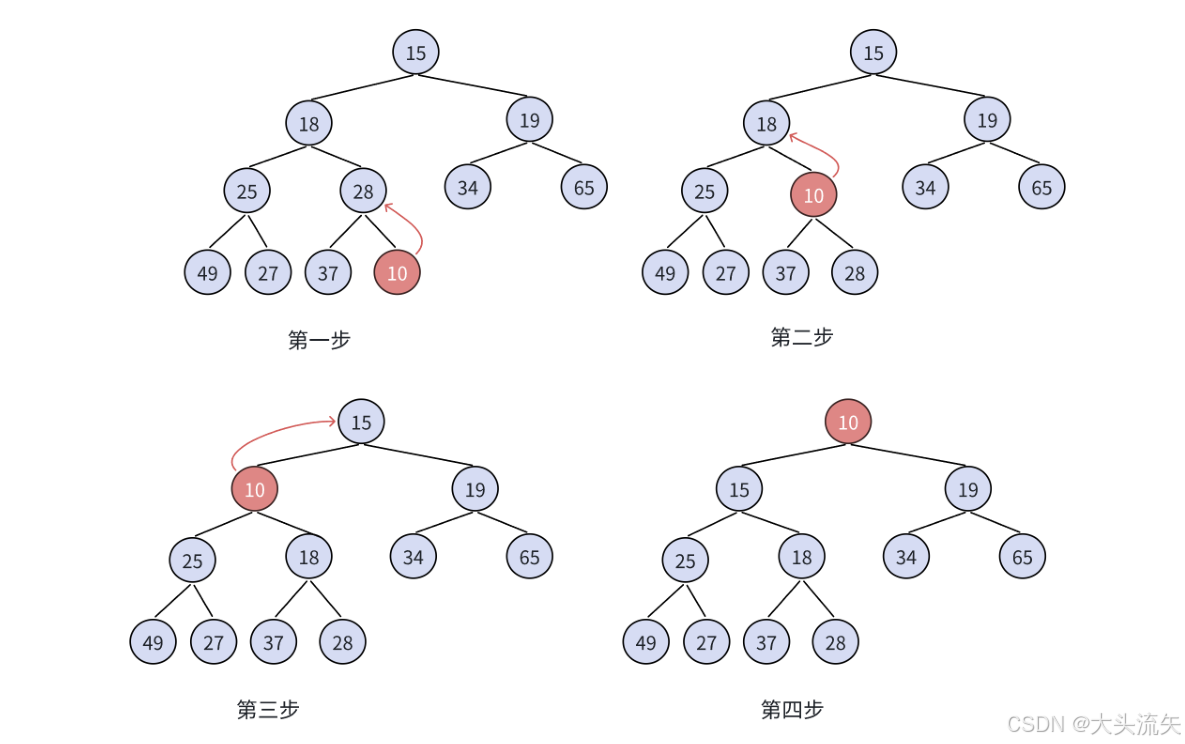
这就是一个利用向上调整法的插入建堆,当数组里面为空时,我们插入的第一个元素就是堆,因为只有一个元素
//向上调整
//参数(数组首元素地址、数组元素个数、要插入堆的位置)
void HeapJustUp(HPDataType* a, int size, int sub)
{
int child = sub;
int parent = (child - 1) / 2;
while (child > 0)
{
//大于 == 大堆
//小于 == 小堆
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}sub尾元素的下标,child就指向了尾元素,parent指向了child的父结点,child为什么小于等于0就接受呢?因为当尾部元素反复与自己的父结点比较交换以后,最后如果到达了根结点,那么就说明该元素此时是堆里最大的元素了,就可以结束循环了
如果在到达根节点之前child就小于parent那么就退出循环,说明此时child已经达到了可以维持堆性质的位置(本来再堆尾拆入一个数,就破坏了堆的性质,要维护堆的性质,就必须让这个新元素来到适合的位置,比如在说在根的左右树的任意一边中比新元素小的就变成新元素的子结点)
大堆小堆(父结点大于子结点/父结点小于子结点)
重点:
- 被插入的数组必须得是堆
- 每次对比交换就是向上走的,所以你要对比交换的父结点必须是堆,子结点可以不是
向上调整建堆代码
//向上调整:建堆
void HeapUpPileup(HPDataType* a, int size, int sub)
{
//为什么要放在一个循环里面?
//因为你每调用一次HeapUp就只会插入一个元素
for (int i = sub; i < size; i++)
{
HeapUp(a, size, i);
}
}我知道可能很多人在看那个向上调整法的时候,里面那个sub还能理解到了这里就有点理解不了了,没事我画一张图你就理解了

向上调整法的时间复杂度
分析:
第1层, 2^0 个结点,需要向上移动0层
第2层, 2^1 个结点,需要向上移动1层
第3层, 2^2 个结点,需要向上移动2层
第4层, 2^3 个结点,需要向上移动3层
......
第h层, 2^(h−1) 个结点,需要向上移动h-1层

向下调整法
接下来思考一下,删除根节点怎么删除?
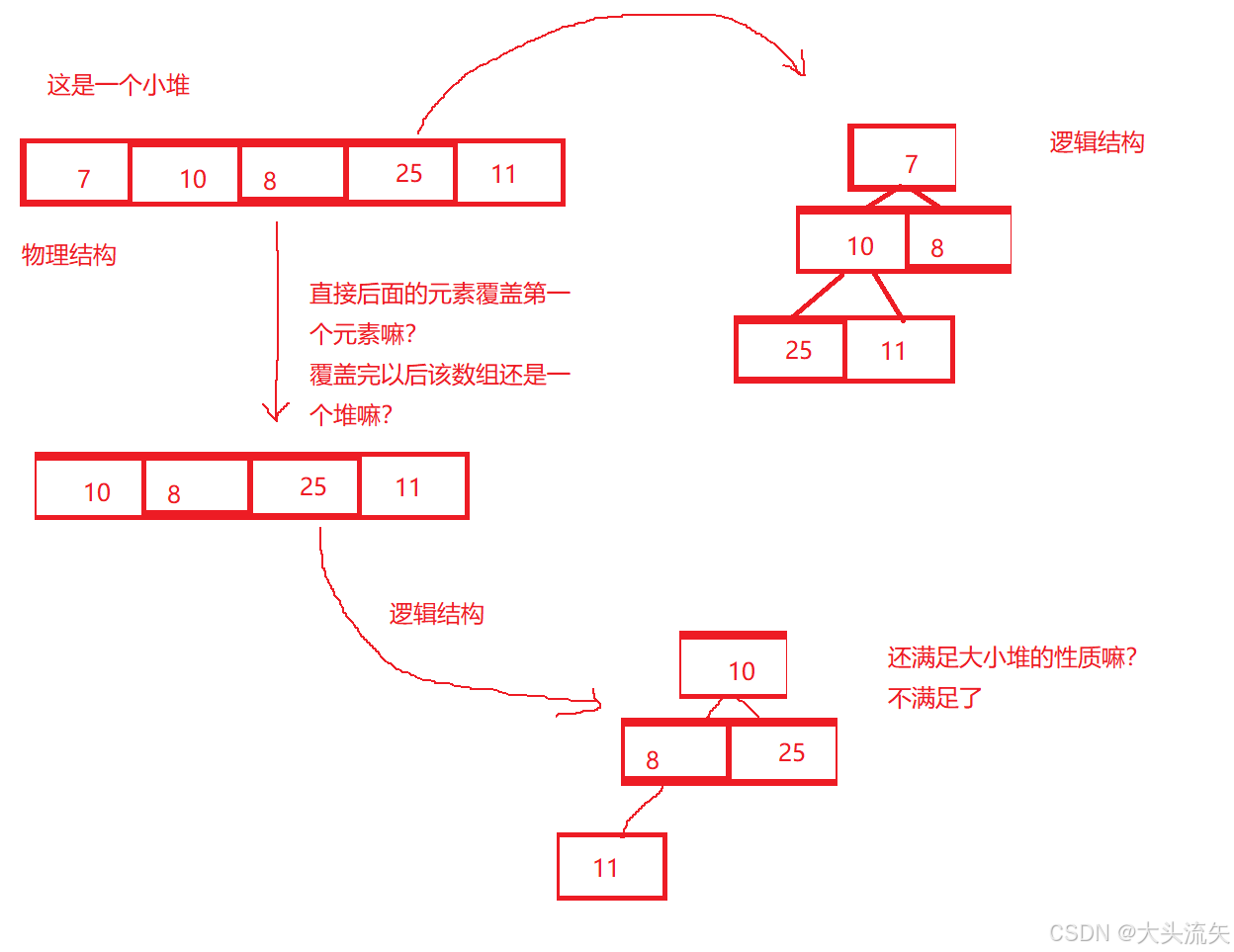
这个时候聪明的小牛肯定会说,我们刚刚不是学了向上调整法嘛,我们重新插入一边就好了,确实这个方法确实可行,但是既然我们现在学了数据结构,那么不是所有可执行可达到目的的代码就是好代码了,我们计算一下刚刚说的那种时间的复杂度:
删除根的元素,后面元素往前移,n个数据移动n-1次
每一移动一次,用向上调整建堆,而它的时间复杂度是
,俩者相乘就是
O(n^2 log n),是不是一下子感觉这个方法很挫了!我直接向后遍历也就O(n^2),所以这个办法是行不通的
办法呢还是有的,看一张图你就悟了
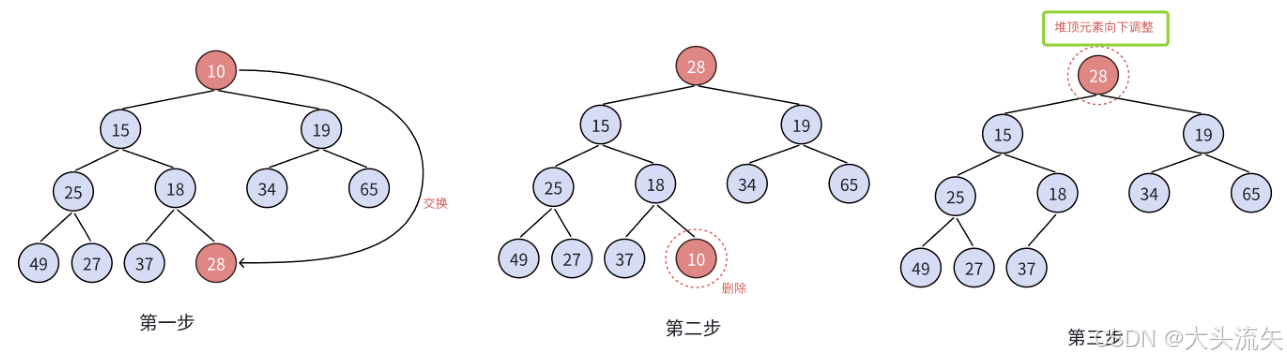
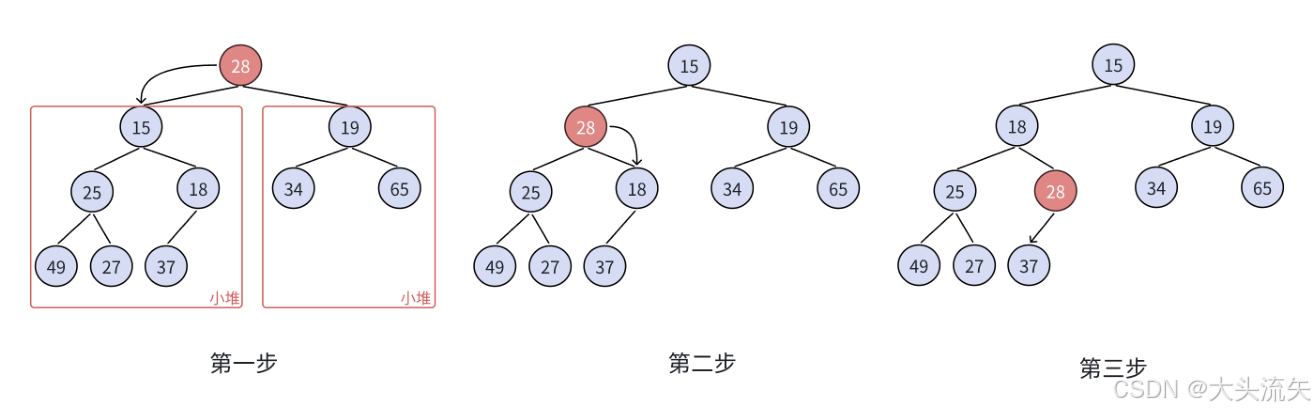
这个流程就是向下调整法,每次都要将首尾元素交换,然后删除尾部即可
重点:
向下调整算法有⼀个前提:左右子树必须是⼀个堆,才能调整。
将堆顶元素与堆中最后⼀个元素进行交换
删除堆中最后⼀个元素
将堆顶元素向下调整到满足堆特性为止
我主要实现的就是第二张图里的步骤,往下对比交换的过程,先讲一下思路:
首尾交换元素这一步可以在外部完成不需要放在HeapDown函数中,我们写的函数应该只处理接收到的下标数据,然后从接收到的下标数据依次往下比较,满足条件就交换,比较完就退出,还要再处理就在调用该函数,其实就是父结点在俩个子结点里对比,这个和向上调整相反,它是子结点和父结点对比
接下来看代码:
//向下调整
//参数(数组首元素地址、数组元素个数、要向下调整的父结点的下标)
void HeapJustDown(int* a, int size, int parent)
{
//先假设左节点是最大的/小
int child = parent * 2 + 1;
while (child < size)
{
//预防非法访问 && 在俩个子结点里选出最大的
if (child + 1 < size && a[child] < a[child + 1])
{
child++;
}
//大于 == 大堆
//小于 == 小堆
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
}
//以上条件都不满足的话,说明已经符合(大/小)堆
else
{
break;
}
parent = child;
child = parent * 2 + 1;
}
}为什么会有一个child + 1 < size 这个条件就是为了防止,非法访问,如果该完全二叉树最后一个叶子节点是左节点呢?你直接a[child] < a[child+1]不就非法访问了
while的结束条件,也是因为该方法是向下调整的,所以child的值>=元素个数的时候,说明child已经比较完了
向下调整法建堆
接下来再讲一下向下调整法建堆,首先,我们先理一下向下建堆的前提是什么:
- 左右树为堆
对这是很重要的一点,那么我们拿到一个数组,怎么把它里的数据整理成堆呢?
我们想象一下只有一个结点的时候既可以是大堆也可是是小堆,那么如果是最后这一层的叶子结点呢?我们是不是也可以将最后一层看作一个堆呢,因为我们用向下调整只要保证左右子树是堆就可以了,这样子的话,我们就可以将最后一个元素的下标传过去,然后让他的父结点和俩个子节点对比,符合条件的就交换,接下来我就画一个流程图
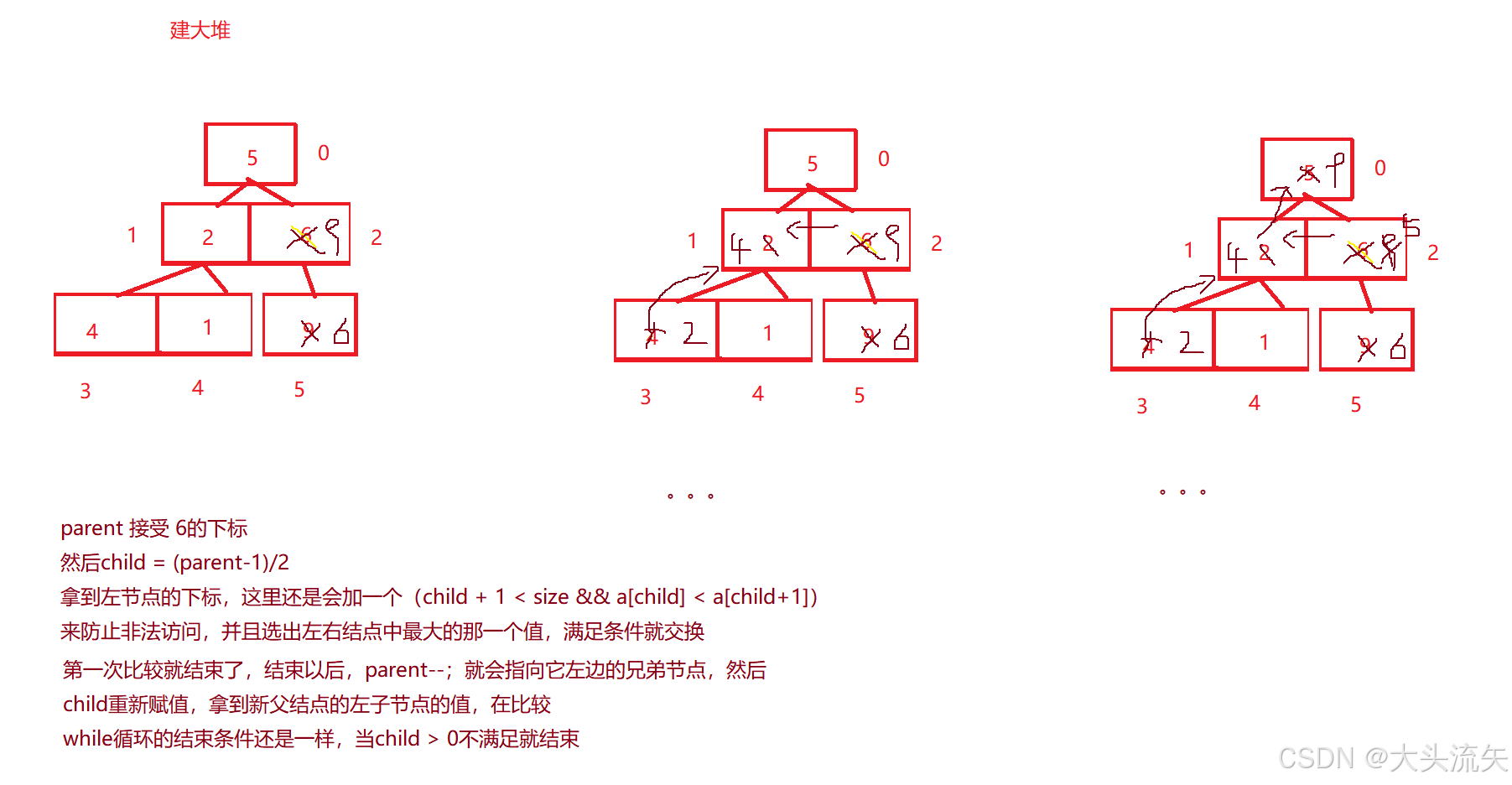
所以我们这里如果用向下调整建堆的话,还是会用到for循环
//向下调整:建堆
void HeapDownPileup(int* a,int size)
{
//每次传入的都是子节点的父节点(size为元素个数)
//为什么是size-1-1呢,size-1是定位到最后一个元素的下标
//在-1除2就是为了拿到该下标元素的父结点下标
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{
HeapDown(a, size, i);
}
}向下调整建堆的时间复杂度
分析:
第1层, 20 个结点,需要向下移动h-1层
第2层, 21 个结点,需要向下移动h-2层
第3层, 22 个结点,需要向下移动h-3层
第4层, 23 个结点,需要向下移动h-4层
......
第h-1层, 2h−2 个结点,需要向下移动1层

当n非常非常大的时候,logn是可以忽略不计的,不信可以计算看一下~
堆插入
有了以上的基础在来写堆插入就很简单了
// 堆的插入(向上调整建堆)
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
//判断此时的capacity是否初始化过
if (hp->capacity == hp->size)
{
int new_capacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * new_capacity);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
hp->capacity = new_capacity;
hp->a = tmp;
}
//赋值
hp->a[hp->size] = x;
hp->size++;
HeapJustUp(hp->a, hp->size);
}这里用的就是向上调整法的插入思维,可以做到边存变建堆
如果是向下调整法建堆的话,就得等所有的数据都已经入到数组以后,你在用一个for循环来建堆
堆删除
堆删除的话主要就是用向下调整的方法来实现:
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
HeapJustDown(hp->a, hp->size,hp->capacity);
hp->size--;
}堆排序
其实有了前面那些理解堆排序也是很简单的,就是利用了堆删除的思想,但是要注意的是
必须有现成的堆
升序 --- 建大堆
降序 --- 建小堆
我们想想堆删除的思想是什么?把根和尾结点交换对吧,然后再利用向下调整法把次大的元素弄到根的位置,然后我们在交换,但是注意这次的交换就不是和尾结点交换了,而是尾结点-1的位置交换,然后在向下调整,直到根和要交换的位置重叠,就可以退出循环了(这里的循环指的是for大循环,不是HespJustDown中的while),但是我们每次传入的数组元素个数也要减1,不然你往后放的最大值都会被调整上去,导致整个堆的性质丢失
void HeapSort(int* a, int size, int parent)
{
assert(a);
for (int i = size - 1; i >= 0; i--)
{
parent = 0;
Swap(&a[0], &a[i]);
int child = parent * 2 + 1;
while (child < i)
{
//预防非法访问 && 在俩个子结点里选出最大的
if (child + 1 < i && a[child] < a[child + 1])
{
child++;
}
//大于 == 大堆
//小于 == 小堆
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
}
//以上条件都不满足的话,说明已经符合(大/小)堆
else
{
break;
}
parent = child;
child = parent * 2 + 1;
}
}
}Top K 问题
有了以上基础,Top K问题对我们来说就是小case
TOP-K问题:即求数据结合中前K个最⼤的元素或者最⼩的元素,⼀般情况下数据量都⽐较⼤。
⽐如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的⽅式就是排序,但是:如果数据量⾮常⼤,排序就不太可取了
(可能数据都不能⼀下⼦全部加载到内存中)。最佳的⽅式就是⽤堆来解决,基本思路如下:
1)⽤数据集合中前K个元素来建堆
前k个最⼤的元素,则建⼩堆(因为要堆内最小的元素,先替换出,然后再把次小的放在堆顶)
前k个最⼩的元素,则建⼤堆
2)⽤剩余的N-K个元素依次与堆顶元素来⽐较,不满⾜则替换堆顶元素
将剩余N-K个元素依次与堆顶元素⽐完之后,堆中剩余的K个元素就是所求的前K个最⼩或者最⼤的元素
总体的思想就是,先从文档中按顺序拿取k个数据,然后用向下调整法建小堆(当然这个看你取k个是最大值还是最小值),最后接着拿文档内剩余的数据和堆顶比较,符合条件的就入堆

void CreateNDate()
{
//先创建一个存有1000000个随机数据的文档
int n = 1000000;
FILE* file = fopen("data.txt", "w");
if (file == NULL)
{
perror("file fail");
exit(-1);
}
srand((unsigned)time(NULL));
for (int i = 0; i < n; i++)
{
// 生成-50000到49999的随机数
int x = (rand() % 100000) - 50000+i;
fprintf(file, "%d\n", x);
}
fclose(file);
file = NULL;
}void PrintTopK(const char* file, int k)
{
//先建立k个元素的堆
FILE* f = fopen(file, "r");
if (f == NULL)
{
perror("f fail");
exit(-1);
}
//建立一个k大小的数组
int* arr = (int*)malloc(sizeof(int) * k);
if (arr == NULL)
{
perror("malloc fail");
exit(-1);
}
//先将文档中的k个数值存入数组中
for (int i = 0; i < k; i++)
{
fscanf(f, "%d", &arr[i]);
}
//将数组中的数据用向下调整的方法整理成小堆(因为我们这里Top k 求的是最大值)
HeapDownPileup(arr, k);
//将文档中剩余的第k+1个与小堆的堆顶去比较,大于就入堆顶
for (int i = 0; i < 1000000 - k; i++)
{
int tmp = 0;
fscanf(f, "%d", &tmp);
if (tmp > arr[0])
{
arr[0] = tmp;
HeapDown(arr, k, 0);
}
}
//将堆里的数据整理成降序的
HeapSort(arr, k, 0);
//打印前k个值
for (int i = 0; i < k; i++)
{
printf("%d ", arr[i]);
}
fclose(f);
free(arr);
}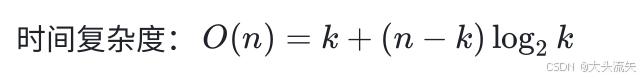
其实你了解了思路以后再去看代码,真的是非常好的一种学习方式
总结
向上调整法:
- 适用场景:边存边建堆(动态插入,如优先级队列、数据流 TopK)。
- 调整方向:自下而上,新元素和父节点比较交换。
- 核心前提:父结点所在子树满足堆性质。
- 操作特点:针对单一元素调整,多元素需外层循环;构建堆时间复杂度
向下调整法:
- 适用场景:已存完数据的静态数组建堆(如堆排序初始堆、批量数据建堆)。
- 调整方向:自上而下,当前节点和左右子节点比较交换。
- 核心前提:左右子树均满足堆性质。
- 操作特点:针对单一元素调整,多元素需从最后一个非叶子节点往前循环;构建堆时间复杂度 O(n),效率更优。




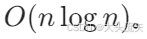
















 1312
1312

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








