Nakagami-m 分布——基础知识

12345balabala

已于 2022-11-02 20:56:21 修改

阅读量1.8w

点赞数 12

分类专栏：常用数学笔记文章标签：人工智能

于 2020-04-10 16:38:56 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/ma123rui/article/details/105436076

版权

常用数学笔记专栏收录该内容

15 篇文章

订阅专栏

1、定义

It has two parameters: a shape parameter and a second parameter controlling spread $\Omega >0$ .

2、参数估计

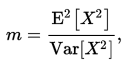
3、 Nakagami-m 分布与 gamma distribution 的关系

（1）论文中记录的

is a Nakagami-m distribution with fading parameter . 有

于是，得到：

也就是说，一个随机变量是服从Nakagami-m分布的，那么它的模值的平方服从伽马分布。

$\begin{array}{l} {h_{AE}} \sim Nakagami\left( {{m_E},1} \right),m = {m_E},\Omega = 1\\ {\left| {{h_{AE}}} \right|^2} \sim Gamma\left( {k = {m_E},\theta = \frac{1}{{{m_E}}}} \right)\;or\;Gamma\left( {\alpha = {m_E},\beta = {m_E}} \right)\\ {{\bar \gamma }_E}{\left| {{h_{AE}}} \right|^2} \sim Gamma\left( {k = {m_E},\theta = \frac{{{{\bar \gamma }_E}}}{{{m_E}}}} \right)\;or\;Gamma\left( {\alpha = {m_E},\beta = \frac{{{m_E}}}{{{{\bar \gamma }_E}}}} \right) \end{array}$

其中，

例如：

All channels are characterized by Nakagami-m fading.

《When NOMA Multiplexing Meets Symbiotic Ambient Backscatter Communication- Outage Analysis》

(2) 维基百科说法

评论 3

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。