算法基础（三）（共有20道例题）

七、数学知识

（一）质数

1. 质数（素数） 的定义：
   
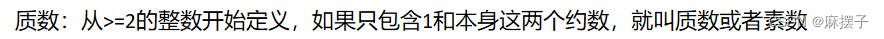
2. 互质的定义：除了1以外，两个没有其他共同质因子的正整数称为互质，比如3和7互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。
3. 约数（因数） 的定义：约数又称为因数。整数a除以整数b (b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。 a称为b的倍数，b称为a的约数。
4. 合数的定义：合数是指在>=2的整数中除了能被1和本身整除外，还能被其他正整数（0除外）整除的数。 与之相对的是质数，而1既不属于质数也不属于合数 。最小的合数是4。
5. 质因数的定义：质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。
   （1）只有一个质因数的正整数为质数。
   举例：5只有1个质因数，5本身。（5是质数）
   （2）质因数就是一个数的约数，并且是质数。
   举例：8=2×2×2，2就是8的质因数，2既是质数又是约数；12=2×2×3，2和3就是12的质因数，2和3既是质数又是约数；
   （3）1没有质因数。
   2、4、8、16等只有1个质因子：2。（2是质数，4 =2²，8 = 2³，如此类推）
6. 定理1：一个合数n分解而成的质因数最多只包含一个大于$\sqrt{n}$的质因数。
   举例：$n=99=11\times 3^2$，其中11大于$\sqrt{99}$。
   反证法：若n可以被分解成两个大于$\sqrt{n}$的质因数,则这两个质因数相乘的结果大于n,与事实矛盾
7. 定理2：算术基本定理（唯一分解定理）：正整数的因数分解可将正整数表示为一连串的质因数相乘，任何一个大于 1 数都能分解为素数幂次方乘积的形式, 即每一个数n都能分解成
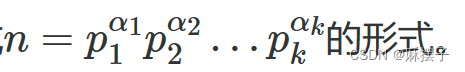
   质因数如重复可以用指数表示。根据算术基本定理，任何正整数皆有独一无二的质因数分解式。
   证明：证明: 若一个数是素数。定理显然成立。那么, 若一个数n是合数, 意味着它有因子, 即可以得到n=n1n2, 其中n1和n2都严格小于n。若n1和n2都不是素数。那按照同样的方式。n1和n2也可以各自分解为一些因子的乘积, 且因子都严格小于它们。那么, 由于n是有限的。到最后n只会分解成为$p{1}^{\alpha 1}$$p{2}^{\alpha 2}$…$p{k}^{\alpha }k$的形式。且p1
   , p2, … , pk都为素数(不全为素数的话就继续往下分)。(证毕)

例题1：试除法判定质数

题目 难度：简单
方法一：暴力，时间复杂度$O(n)$

bool isPrime(int x) 
{
   
  if (x < 2) return false;
  for (int i = 2; i < x; ++i)
  {
   
     if (a % i == 0) return false;
   }
  return true;
}

方法二：试除法
暴力做法其实已经很简单了，但是如果 x 是 a 的约数，那么 $\frac{a}{x}$也是 a 的约数。
所以对于每一对 $(x,\frac{a}{x})$，只需要检验其中的一个就好了。为了方便起见，我们之考察每一对里面小的那个数。不难发现，所有这些较小数就是$[1,\sqrt{a}]$ 这个区间里的数。因从时间复杂度从暴力法的$O(n)$，降到$O(\sqrt{n})$

#include<iostream>
using namespace std;

bool is_prime(int x)
{
   
    if(x<2) return false;
    for(int i=2;i<= x/i;i++)
    {
   
        if(x%i==0) return false;
    }
    return true;
}

int main()
{
   
    int n;
    cin>>n;
    while(n--)
    {
   
        int x;
        cin>>x;
            
        if(is_prime(x))
        cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

例题2：分解质因数。给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数

题目 难度：简单
试除法：时间复杂度$O(\sqrt{n})$

#include <iostream>
#include <algorithm>

using namespace std;

void divide(int x)
{
   
    for (int i = 2; i <= x / i; i ++ )
    {
   
        if (x % i == 0)//说明i是x的因数。一个数除了1之外，他最小因数一定是质数，所以这里遇到的第一个能整除x的i一定是质数。
        {
   
            int s = 0;//指数
            while (x % i == 0) x /= i, s ++ ;//求i的指数s，比如x=10，i=2，s=1；x=10/2=5
            cout << i << ' ' << s << endl;
        }
    }
    if (x > 1) cout << x << ' ' << 1 << endl;
    //把这个最小质因数i1除干净了之后得到一个新的数x2
    //这个新的数x2的最小质因数i2肯定比之前的最小质因数i1大，因为比之前小的都被除干净了，同理新的数x2的最小因数又是质因数。
    //比如100=2*2*5*5，第一个最小质因数i1=2，除干净后得到新的数x2=25，这时i就从3开始for循环,得到新的数的最小质因数i2=5
    cout << endl;
}

int main()
{
   
    int n;
    cin >> n;
    while (n -- )
    {
   
        int x;
        cin >> x;
        divide(x);
    }
    return 0;
}

例题3：筛质数。给定一个正整数 n，请你求出 1∼n 中质数的个数。

题目 难度：简单

朴素筛法

1.做法：为了找出1~n中的质数，把 2 ~ (n-1)中的所有的数的倍数都标记上，最后没有被标记的数就是质数。
2.原理：假定有一个数p未被 2 ~ (p-1)中的数标记过，那么说明，不存在 2~(p-1)中的任何一个数的倍数是p，也就是说p不是 2 ~ (p-1)中的任何数的倍数，也就是说2 ~ (p-1)中不存在p的约数，因此，根据质数的定义可知：p是质数。
3.时间复杂度：当i=2时，循环了n/2次，当i=3时，循环了n/3次……当i=n时，循环了1次。所以
$n/2+n/3+n/4\dots \dots n/n=n(1/2+1/3+1/4\dots \dots +1/n)=n（lnn+c）$
调和级数:当n趋近于正无穷的时候，$1/2+1/3+1/4+1/5+\dots +1/n=lnn+c$
底数越大,log数越小，所以$nlog{e}^n<nlog{2}^n$
最后得到时间复杂度约为$O(nlogn)$。

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
bool tag[N];//用来打标记，默认是false
int prime[N];
int cnt=0;

void get_prime(int n)
{
   
    for(int i=2;i<=n;i++)
    {
   
        if (tag[i]==true) continue;//如果标记为true，直接进行下一次for循环
        prime[cnt++] = i;;//2，3，5，7，11……是质数，计入
        for(int j=i+i;j<=n;j+=i) tag[j]=true;//给j的倍数（2的倍数：4，6，8，12……。3的倍数：6，9，12，15……。）打上标签true，代表j的倍数是合数
    }
}

int main()
{
   
    cin>>n;    
    get_prime(n);
    
    cout<<cnt;
    return 0;
}

埃氏筛法

1.做法：为了找出 1 ~ n 中的质数，把 2 ~ (n-1) 中的所有素数的倍数都标记上，最后没有被标记的数就是1 ~ n 中的质数。
2.原理：在朴素筛法的过程中只用质数项去筛。
埃氏筛法的时间复杂度的简化来源于只需把素数的倍数删掉。这样的话就可以少筛很大一部分数。因为每个合数都是素数的倍数，比如$4=2\ast 2，6=2\ast 3，8=2\ast 4，9=3\ast 3$。
3.时间复杂度：是 $O(n$