数据安全之散列函数（三）- MD4 算法原理详解

MD5 是 Message-Digest Algorithm 信息摘要算法的简写，是一种无密钥的迭代 hash 算法。OpenJDK 中 MD5 的实现类 org.bouncycastle.crypto.digests.MD5Digest，《Handbook of Applied Cryptography》 这本书的第 346 - 347 对 MD5 算法进行了详细的描述。

Chapter 9 - Hash Functions and Data Integrity

MD4 算法详解

在介绍 MD5 之前我们首先来介绍下 MD4算法，虽然 MD4 算法已经不再安全，但是 MD4 算法是大部分 hash 算法的基础，MD5 也是在 MD4 算法的基础上做了一些优化而来的。
MD4 算法输入是任意长度的数据，得到的结果是 128bit 的哈希值。算法处理流程如下：

“2.预处理”部分我们在上一篇文章中已经讲了。数据安全之散列函数（二）- 数据分组与数据填充。
MD4 每个分块分块大小为 512bit ，经过预处理后，会得到一组 512bit 长度的数据块$x_1,x_2...x_n$。
“3.迭代处理”部分的，就是循环将 $x_n$ 和上一轮的结果进行计算得到新的结果。

初始向量（IV）

我们在第一轮计算的时候还没有上一轮的数据怎么办？这时候就要定义一组初始的数据，用于第一轮计算。这组数据就叫做初始向量（IV）。MD4 中定义如下，每个数据 32bit 总共 128bit：
$h_1=0x67452301$,
$h_2=0xefcdab89$,
$h_3=0x98badcfe$,
$h_4=0x10325476$

数据分块

首先我们来看第一块 512bit 数据的操作。每一块数据被切分成 16 个 32bit 的小块。这 16 个 32bit 的数据我们定义为 $X$, 如$X[0]$就代表下面第 0 块的数据。

定义常量

再来定义 3 组常量，后面计算中会用到：

1. 定义 32-bit 附加值常量 $y$：

$y[j]=0,0\le j\le 15$;
$y[j]=0x5a827999,16\le j\le 31;(2的平方根前32-bit)$;
$y[j]=0x6ed9eba1,32\le j\le 47;(3的平方根前32-bit)$;

2. 定义原始输入值访问顺序常量 $z$:

$z[\mathrm{0..15}]=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]$;
$z[\mathrm{16..31}]=[0,4,8,12,1,5,9,13,2,6,10,14,3,7,11,15]$;
$z[\mathrm{32..47}]=[0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15]$.

3. 最后定义每一个位置循环左移的位数常量 $s$:

$s[\mathrm{0..15}]=[3,7,11,19,3,7,11,19,3,7,11,19,3,7,11,19],$
$s[\mathrm{16..31}]=[3,5,9,13,3,5,9,13,3,5,9,13,3,5,9,13],$
$s[\mathrm{32..47}]=[3,9,11,15,3,9,11,15,3,9,11,15,3,9,11,15].$

循环计算

循环变量为 $j$ 取值范围为 $0\le j\le 47$。
$j$取值在 $0\le j\le 15$，$16\le j\le 31$, $32\le j\le 47$ 三个区间分别代表三个不同的轮次。

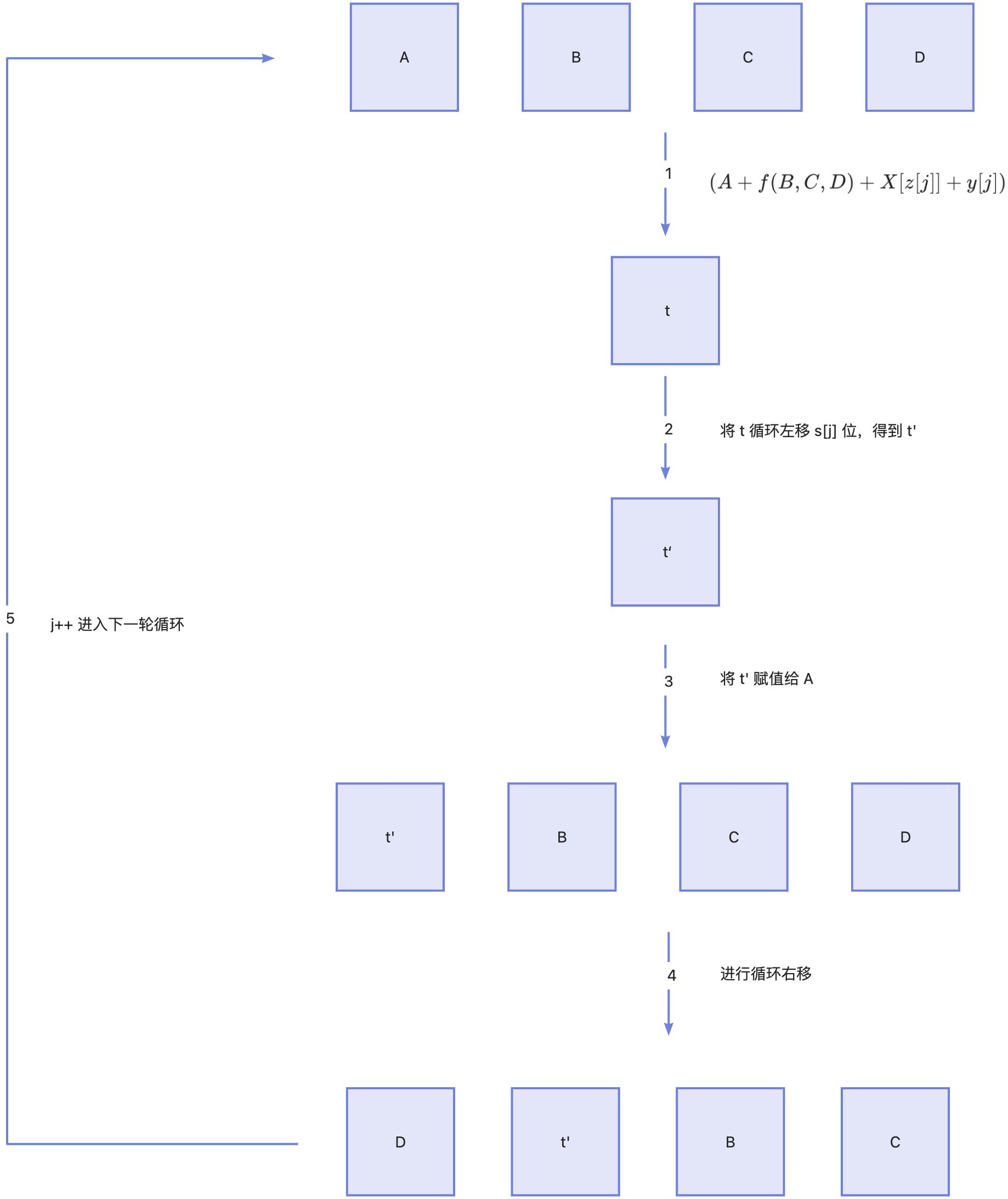
第一轮 $0\le j\le 15$， 上图所示。
当 $j=0$时，还没有上一轮的数据，所以 $A,B,C,D$ 使用初始化向量（IV）$h_0,h_1,h_2,h_3$进行赋值。

1. 根据公式 $(A+f(B,C,D)+X[z[j]]+y[j])$ 计算出 $t$, $z$和 $y$为「常量定义」章节中定义的常量，$X$则为「数据分块」章节中的原始数据数组。 $f(B,C,D)$则为固定函数。

比如$j=0$ 时 $z[0]=0，y[0]=0,X[z[0]]$就是原始第 0 块数据。

2. 将$t$ 进行循环左移 $s[j]$位，得到 $t^{\prime }$
3. 将 $t^{\prime }$ 赋值给 A
4. 将结果数据进行循环右移
5. 将 $D,t^{\prime },B,C$ 赋值给 $A,B,C,D$ 同时 j++ 进入下一轮计算

第二轮和第三轮和第一轮计算方式相同，这是$f(B,C,D)$的函数不一样。
第一轮函数 $f$ 为 (B & C) | ((~ B) & D)
第二轮函数 $g$ 为 (B & C) ｜ (B & D) ｜ (C & D)
第二轮函数 $h$ 为 B ^ C ^ D

经过 48 轮的运算，最终得到的 $A,B,C,D$ 值合并，就为 MD4 算法计算出的哈希值。

下一篇文章，我们将来详细解析常用的 MD5 算法，请大家点赞、关注不迷路。

系列文章：

数据安全之散列函数（一）-了解散列函数

数据安全之散列函数（二）- 数据分组与数据填充

数据安全之散列函数（三）- MD4 算法原理详解

数据安全之散列函数（四）- MD5 算法原理详解

数据安全之散列函数（五）- MD5 JDK 源码解析