完美洗牌的秘密（十六）——（反）完美洗牌第三定理的应用一（15张Australian发牌找4Ace）...-CSDN博客

这个魔术是从我的朋友常天天那里交流来的，一个anti-faro shuffle奇数张和Australian deal的完美结合，具体出处如果有朋友知道还望指正。不过无论如何，这又是一个让我及其震撼的数学魔术演出。因为它不仅仅和我们这个系列的主题完美洗牌有着很大的关系，而且还成功地串联到之前我们讲约瑟夫问题时候的结论。而可以联系二者的点就在于它们的核心——二进制表示数的运算。

数学原理

整个魔术效果是从一小叠观众选到的牌中变出4个Ace，那一共是15张牌，接着我们来复盘一下整个过程中的操作：

1. 选出15张牌，切牌；

2. 发牌成两叠，再任意顺序收起来；

3. 再执行一次2，中间可以穿插任意次切牌；

4. 最后切牌，然后执行Australian Deal，手里剩下最后4张为Ace。

因为中间涉及到很多次观众的切牌操作，有很多不可控因素，虽然最后的约瑟夫问题的过程可以清晰地推导，但是最开始用错数学模型的我还是绞尽脑汁没有摸到门道。一开始，我总是去尝试用完美洗牌第一定理来理解一开始4张假设相邻的Ace最后会出现在什么地方，切牌以后对其位置有什么影响。却发现，中间涉及的分支太多，因为观众任意切牌张数的这个变量的引入，使得压根没法判断每次逆完美洗牌到底是哪些牌处在了哪一叠，因为随意合起来，还不太知道是out还是in。

当然你把所有的情况都列举出来，还是可以解决的，不过这是计算机人的思路，数学人一定要找到更合适的数学模型去切中要害地从根本上解决一个问题。

没错，这里用到的，就是完美洗牌第三定理，切牌这件事把每张牌的位置索引都改变了，但是如果把牌叠看成首尾相接的环，那相当于什么都没有做。此时我们关心的也不再是绝对的位置坐标，而是两两牌之间相对位置的变化，而它的规律完美洗牌第三定理讲得很清楚了。

因为整个牌叠的张数是15，是奇数，符合完美洗牌第三定理的要求。我们进行的相当于是两次anti faro shuffle，中间穿插的若干次切牌不改变任意两张牌之间的有向距离，因此，对于初始时候原本处在相邻位置的4个Ace中相邻的任意两个，经过这番操作以后有：

a(i + 1) - ai == 4(mod 15)

也即，这4个Ace以一个间隔为4的新的子序列的形式重新存在于整个牌叠了，这确实是一个在牌环的模型下比较不错的一个结论。但是又怎么把它和约瑟夫问题最后留下来的牌之间扯上关系呢？

我们不妨来复习一下约瑟夫问题的结论：

一叠张数的二进制表达为n = 1b1b2......bm位数为(b + 1)的牌叠，执行0相位周期为2的约瑟夫问题时，最后留下的牌的二进制表达为n << 1 = b1b2......bm0。

接着我们还讲过一个推论，其倒数第2个落下和往前若干张的位置为末位为b2b3......bm0为结尾的且索引在n - 1以内的数从大到小的排列，再往前则取末位为b3b4......bm0，以此类推即可得到全部约瑟夫问题数牌后所有倒数落下的牌的索引规律，而这恰好就是留下牌叠的正向排列。

没错，我们约瑟夫问题除了给出了最后一张牌位置的公式，还可以给出整个排列，并且其规律也是足够清晰明了的，那就是逐步以 n << 1的尾数为要求数的倒序遍历即为最终的序列结果。

那这种性质到底有什么好处呢？

仔细观察可以发现，一个二进制表达的数，如果末A位相同，最多A + B位，那么这些数应该最小距离为2 ^ A，个数有2 ^ B，就像一组B位数，都乘以了2 ^ A而已。因此，约瑟夫问题中的一串串留下来的数到过来看，应该是一组组这样尾数相同，即各自相差定值的一个个片段，不信我随便给你举一个例子：

n = 13 = 1101

n << 1 = 1010

此时，约瑟夫问题走完以后，其牌叠顺序（和倒数放置顺序等价）为：

1010

以上为结尾为1010的1个值

0010

以上为结尾为0010的1个值，合起来结尾为010的2个值

0110

以上为结尾为110的1个值，1110超出范围而不存在，合起来结尾为10的3个值。

1100

1000

0100

0000

以上为结尾为00的四个，合起来结尾为0的7个值。

1011

1001

0111

0101

0011

0001

以上为结尾1的6个值，缺了1101和1111，合起来就是为空的13个值。

如果把它们画成一棵二叉树应该就更明白了：

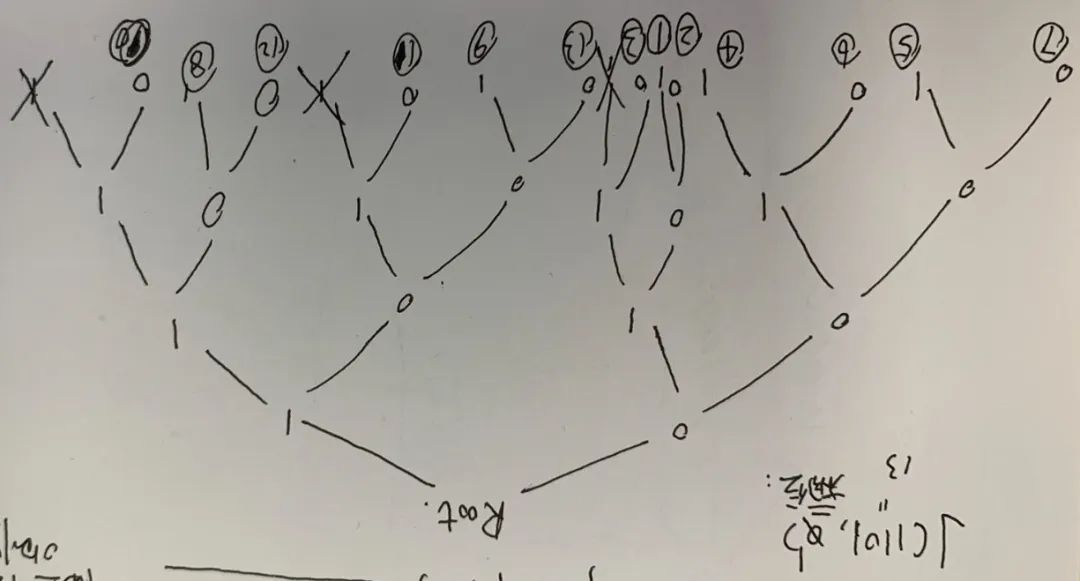
这里的遍历算法复杂度也分析在上面了，是nlogn，即遍历一棵子树的复杂度。

没错，约瑟夫过程的本质，其实就是对一个序列全部索引值的一次遍历（这句其实是废话，因为排列的定义已经说明了这一点）。而且遍历方式是，在一棵含有全部0~(n - 1)这n个数的二进制倒序索引对应的路径的二叉树上，用叶子表示其每个值。从排列张数n << 1对应的那个叶子开始，不断寻找其相邻二叉树节点遍历，遍历方式为从大到小的逆序（因为是倒着数的，所以实际拿走顺序是从小到大），如果没有或者遍历完成后，就直接找到其父亲进行下一次遍历，直到达到根节点即为所求。依次遍历所有叶子节点的顺序即为约瑟夫过程形成牌叠的排列顺序。因为是从底累积到顶的，所以实际排序还要倒过来。

我做梦也没有想到，第一次惊讶于这个魔术通过二进制原理把约瑟夫问题和完美洗牌结合在了一起。而当我终于有时间静下心来写这个魔术的时候，却发现了约瑟夫问题的惊天大秘密！

具体到这个魔术，其实就十分简单了，在n = 15的情况下，这是一棵满二叉树，遍历从1110的逆序，也就是0111所在的叶子节点开始，按照如上的规则进行。于是很容易知道，最后留下的4张牌，也就是约瑟夫过程形成的新牌叠的顶端的4张牌，恰好就是尾数为10的4张，同处在一个节点上，它们相距为4，刚好和前面反完美洗牌的结果对应，只差一个常数！

注意这里整体张数是15，即一个给定4位二进制数的最大值这一点十分重要。它使得遍历时候不会出现节点缺失而跳过，而是直接能够得到需要的结果！

这个常数也非常好确定，在15张牌中4张相距为4的子序列中，只有顶到底两张是相距4 * 3(mod 15) = - 3的，为负值，因此我们只需要找到相距为3的中间两张牌的起点即为底牌。它也是等效的遍历起点，因为剩下的3张牌刚好是它依次减4的结果，符合上面的遍历条件，或者尾数10也揭示了，相位就是10 = 2，即要让4张相距的Ace的首位处在0010 = 2处，即前面有2张。所以，我们把这个底牌置于遍历的起点位置1110，也就是最后一张，一切就大功告成了！！！

最后提示一点，我们这里执行的，其实是逆完美洗牌加上了一个reverse操作，而大家知道，reverse是一个阶次为2的操作，2次会回到自身（当然这里并不一定可以，因为排列群并不都是阿贝尔群）。不过这里不管会不会回到自身，一次reverse操作只会导致两张牌的有向距离变成相反数，绝对值不会变！因此绝不影响我们的结论，而变成相反数这一操作在加法群内也是一个阶为2的操作，因此甚至其有向距离的值都会完全不变！

真理尽在掌握！

最后还留一个尾巴，你有没有想过，约瑟夫问题这样看起来的递减操作，是怎么真的和二进制操作联系起来的，背后还有怎样的隐藏结构？下一篇我们继续聊这个魔术更深的数学结构和魔术原理，敬请关注！

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！