第三章、函数的增长 -- 渐近记号

渐近记号、函数与运行时间

$\Theta 记号$

对一个给定的函数$g(n)$，用$\Theta (g(n))$来表示一下函数的集合：
Θ ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 1 、 c 2 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) } \Theta(g(n))=\{f(n):存在正常量c_1、c_2和n_0,\\ 使得对所有n\geq n_0,有0\leq c_1g(n)\leq f(n)\leq c_2g(n)\} Θ(g(n))={f(n):存在正常量c1​、c2​和n0​,使得对所有n≥n0​,有0≤c1​g(n)≤f(n)≤c2​g(n)}

若存在正常量$c_1$和$c_2$，使得对于足够大的$n$，函数$f(n)$能“夹入”$c_{1}g(n)$与$c_{2}g(n)$之间，则$f(n)$属于集合$\Theta (g(n))$。因为$\Theta (g(n))$是一个集合，所以可以记$f(n)\in \Theta (g(n))$，以指出$f(n)$是$\Theta (g(n))$的成员，作为替代，我们通常记$f(n)=\Theta (g(n))$以表达相同的概念。

下图给出了函数$f(n)$与$g(n)$的一幅直观画面，其中$f(n)=\Theta (g(n))$。对在$n_0$及其右边$n$的所有值，$f(n)$的值位于或高于$c_{1}g(n)$且位于或低于$c_{2}g(n)$。换句话说，对所有$n\ge n_0$，函数$f(n)$在一个常量因子内等于$g(n)$。我们称$g(n)$是$f(n)$的一个渐进紧确界。

$\Theta (g(n))$的定义要求每个成员$f(n)\in \Theta (g(n))$均渐近非负，即当$n$足够大时，$f(n)$非负。因此，函数$g(n)$本身必为渐近非负，否则集合$\Theta (g(n))$为空。所以我们假设用渐近记号中的函数都渐近非负。

$O$记号

$\Theta$记号渐近地给出一个函数的上界跟下界。当只有一个渐近上界时，使用$O$记号。
Θ ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ f ( n ) ≤ c g ( n ) } \Theta(g(n))=\{f(n):存在正常量c和n_0,\\ 使得对所有n\geq n_0,有0\leq f(n)\leq cg(n)\} Θ(g(n))={f(n):存在正常量c和n0​,使得对所有n≥n0​,有0≤f(n)≤cg(n)}

$\Omega$记号

正如$O$记号提供了一个函数的渐近上界，$\Omega$记号提供了渐近下界。
Ω ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c g ( n ) ≤ f ( n ) } \Omega(g(n))=\{f(n):存在正常量c和n_0,\\ 使得对所有n\geq n_0,有0\leq cg(n)\leq f(n)\} Ω(g(n))={f(n):存在正常量c和n0​,使得对所有n≥n0​,有0≤cg(n)≤f(n)}

$o$记号

由$O$记号提供的渐近上界可能是也可能不是渐近紧确的。界$2n^2=O(n^2)$是一个渐近紧确的，但是界$2n=O(n^2)$却不是。我们使用$o$记号来表示一个非渐近紧确的上界。

o ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c &gt; 0 ， 存 在 常 量 n 0 &gt; 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ f ( n ) &lt; c g ( n ) } o(g(n))=\{f(n):存在正常量c&gt;0，存在常量n_0&gt;0,\\ 使得对所有n\geq n_0,有0\leq f(n)&lt;cg(n)\} o(g(n))={f(n):存在正常量c>0，存在常量n0​>0,使得对所有n≥n0​,有0≤f(n)<cg(n)}

$\omega$记号

使用$\omega$记号来表示一个非渐近紧确的下界。

ω ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c &gt; 0 ， 存 在 常 量 n 0 &gt; 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c g ( n ) &lt; f ( n ) } \omega(g(n))=\{f(n):存在正常量c&gt;0，存在常量n_0&gt;0,\\ 使得对所有n\geq n_0,有0\leq cg(n)&lt;f(n)\} ω(g(n))={f(n):存在正常量c>0，存在常量n0​>0,使得对所有n≥n0​,有0≤cg(n)<f(n)}

渐近记号的性质

传递性：

如：$$f(n)=\Theta (g(n))且g(n)=\Theta (h(n))蕴含f(n)=\Theta (h(n))$$

其他的也具体有此性质。


自反性：

如：$$f(n)=\Theta (f(n))$$

其他的也具体有此性质。


对称性：

$$f(n)=\Theta (g(n))当且仅当g(n)=\Theta (f(n))$$

转置对称性：

$$\begin{gathered} f(n)=O(g(n))当且仅当g(n)=\Omega (f(n)) \\ f(n)=o(g(n))当且仅当g(n)=\omega (f(n)) \end{gathered}$$

因为这些性质对渐近记号成立，所以可以在两个函数$f$和$g$的渐近比较和两个实数$a$和$b$的比较之间做一种类比。
$$\begin{array}{rl}& f(n)=O(g(n))类似于a\le b\\ & f(n)=\Omega (g(n))类似于a\ge b\\ & f(n)=\Theta (g(n))类似于a=b\\ & f(n)=o(g(n))类似于a<b\\ & f(n)=\omega (g(n))类似于a>b\end{array}$$
然而，不是所有的函数都能用渐近记号：
对于两个函数$f(n)$和$g(n)$，也许$f(n)=O(g(n))$和$f(n)=\Omega (g(n))$都不成立。例如我们不能使用渐近记号来比较函数$n$和$n^{1+sinn}$，因为$n^{1+sinn}$中的幂值在0跟2之间摆动，取介于两者之间的所有值。

对于渐近记号的理解

对于插入排序，可以有插入排序的最坏情况运行时间为$\Theta (n^2)$或$O(n^2)$、$\Omega (n^2)$；插入排序的最好情况运行时间为$\Theta (n)$或$O(n)$、$\Omega (n)$，甚至是$o(n^2)$。

对于归并排序，可以有归并排序的最坏情况运行时间为$\Theta (nlgn)$或$O(nlgn)$、$\Omega (nlgn)$；归并排序的最好情况运行时间为$\Theta (nlgn)$或$O(nlgn)$、$\Omega (nlgn)$。

如果描述某个算法的运行时间为$\Theta (n^2)$，蕴含着该算法的最好情况的运行时间与最坏情况的运行时间都为$\Theta (n^2)$。

如果描述某个算法的运行时间为$O(n^2)$，蕴含着该算法的最坏情况运行时间为$O(n^2)$。

如果描述某个算法的运行时间为$\Omega (n^2)$，蕴含着该算法的最好情况运行时间为$\Omega (n^2)$。

$0.5\ast (f(n)+g(n))\le max(g(n),g(n))\le (f(n)+g(n))$

当$n\ge |a|$，有$(n+a{)}^b\le (2n{)}^b$，所以存在$c=2^b$，$n_0=|a|$，当$n\ge n_0$时，有$0\le (n+a{)}^b\le c(n^b)$，所以$(n+a{)}^b=O(n^b)$。

当$n\ge 2|a|$，有$(n+a{)}^b\ge (n/2{)}^b$，所以存在$c=(1/2{)}^b$，$n_0=2|a|$，当$n\ge n_0$时，有$0\le c(n^b)\le (n+a{)}^b$，所以$(n+a{)}^b=\Omega (n^b)$。

所以$(n+a{)}^b=\Theta (n^b)$。

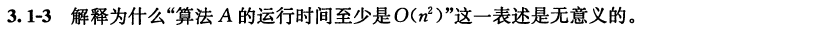
因为形容一个算法的运行时间是$O(n^2)$，也就意味着在$n\ge 某个n_0$时，该算法在[$0，c{n}^2$]的范围内，所以也就是用$O$记号来形容一个算法的运行时间时，蕴涵着的是该算法的最坏情况运行时间，而至少的意思是该算法的最好情况运行时间，二者是相冲突的。

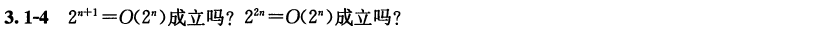
$2^n+1=2\ast 2^n$，所以$2^n+1=\Theta (2^n)$，所以$2^n=O(n^2)$。
$2^{2n}=2^n\ast 2^n$，可以看到并没有常数$c$可以使$2^{2n}\le c\ast 2^n$。

因为$f(n)=\Theta (g(n))$，所以存在正常量$c_1,c_2,n_0$，使得对所有$n\ge n_0$，有$0\le c_{1}g(n)\le f(n)\le c_{2}g(n)$，那么有正常量$c_2,n_0$，使得对所有$n\ge n_0$，有$0\le f(n)\le c_{2}g(n)$；有正常量$c_1,n_0$，使得对所有$n\ge n_0$，有$0\le c_{1}g(n)\le f(n)$。

因为$f(n)=O(g(n))$且$f(n)=\Omega (g(n))$，所以存在正常量$c_2,n_1$，使得对所有$n\ge n_1$，有$0\le f(n)\le c_{2}g(n)$；存在正常量$c_1,n_2$，使得对所有$n\ge n_2$，有$0\le c_{1}g(n)\le f(n)$。那么就有正常量$c_1,c_2,n_0$，其中$n_0=max(n_1,n_2)$，使得对所有$n\ge n_0$，有$0\le c_{1}g(n)\le f(n)\le c_{2}g(n)$。

略。

如果$o(g(n))\cap \omega (g(n))$，则存在$f(n)=o(g(n))且f(n)=\omega (g(n))$，所以有：
$$0=\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=\infty$$
所以$o(g(n))\cap \omega (g(n))$空集。

略。